Вписать - понятие и значение

Рассмотрим что означает понятие и значение слова вписать (информация предоставлена intellect.icu).

1. Сов. переходный смотрите вписывать

1. кого-что во что. Написав, внести, включить куда кто-нибудь В. цитату в тек степень В. фамилию в список. В. славную страницу в историю ( переносное значение ; высокое ). 2. что. В математике: начертить одну фигуру внутри другой с соблюдением определенных условии. В. треугольник в окружность. Вписанный многоугольник.

1. Впишу, впишешь, совершенный вид (к вписывать). 1. кого-что. Записать, внести, включить в список ( официальное ). 2. что. Приписать между, около написанного. Вписать пропущенные слова. 3. что. Вычертить одну фигуру внутри другой так, чтобы она была вписанной (во 2 значение , математика ). Вписать треугольник в окружность.

впишу, впишешь; причастие страдательное (причастие) прошедшее время вписанный, -сан, -а, -о; совершенный вид , переходный

( несовершенный вид вписывать).

1.

Вставить что -либо дополнительно в уже написанный тек степень

Вписать пропущенное слово.

2.

Сделать запись в чем -либо (в тетради, дневнике, журнале и т. падеж ).

Кто, в минуту гнева, не требовал от них {станционных смотрителей} роковой книги, дабы вписать в оную свою бесполезную жалобу. Пушкин, Станционный смотритель.

3. Мат.

Вычертить одну фигуру внутри другой с соблюдением определенных условий.

Вписать треугольник в окружность.

4. переносное значение (обычно в форме причастие страдательное (причастие) прошедшее время ). Расположить, построить и т. падеж таким образом, чтобы что -либо подходило к окружающему, гармонировало с ним.

Только отсюда, с высоты, было видно, как удачно вписан канал в рельеф местности. Паустовский, Героический юго-восток.

- вписать новую страницу

Часть речи

Глагол (инфинитив)

Синонимы

записать, включенный, включивший, записанный, вставленный, внесенный, занесенный, поместивший, прописавший, прописанный, вовлекший, вовлеченный, вселивший, проставивший, проставленный, привнесший, внушивший, поселивший, втащивший, протащивший, впечатавший, пронесший, поставивший, взнесший, вперший, втаскавший, придавший, занесший, вложивший, давший

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "вписать":
аббатствовать, абдуцировать, абецедировать, аблактировать, абонировать, абордировать, абрютировать, абсолютизировать, абсолютировать, абсорбировать, двадцать, имплантировать, исчёркать, мать, начёркать, перечёркать, тридцать, чёркать, щебетать

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "вписать" :
кивипыать, нихоряать, чесолйать, менявоать, кибоныать, нотазоать, тарынаать, перядуать.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Вписать" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-В230, для metaphone-"фписат" и для double-metaphone FPST.

См. также

... Теорема Сторона a правильного связана с радиусом r вписанной окружности . формулой Доказательство Теорема доказана ... (Планометрия)

... Многогранник называется вписанным в шар , если все его вершины лежат . на поверхности шара Многогранник называется описанным около шара ... (Стереометрия)

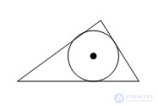... Окружность называется вписанной в треугольник , если она касается через все . его сторон Теорема Центр окружности , вписанной в треугольник , является точкой пересечения его биссектрис . Доказательство Пусть ABC данный , O – центр вписанной ... (Планометрия)

... , вписанный в окружность основания конуса , а вершиной является вершина .конуса Боковые ребра пирамиды , вписанной в конус , являются образующими конуса Касательной плоскостью к конусу называется плоскость , проходящая ... ... Плоскости боковых граней описанной пирамиды являются касательными плоскостями конуса Пирамидой , вписанной в конус , называется такая пирамида , основание которой есть. многоугольник , вписанный в окружность основания конуса ... (Стереометрия)

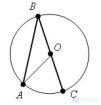... соответствующего центрального угла . Доказательство Пусть есть окружность с центром в точке O и угол . ABC , вписанный в эту окружность , так что одна из сторон .угла проходит через центр окружности Соединим точку ... (Планометрия)

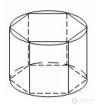... Призмой , вписанной в цилиндр , называется такая призма , у которой плоскостями . оснований являются плоскости оснований цилиндра ... (Стереометрия)

---

---