1. Нареч.
2. Употребляется при подчеркивании высокой степени интенсивности действия или состояния; безмерно, очень.
3. а) разговорное, В большом количестве. б) Очень много.
1) в большом количестве, очень много.
С полсотни человек --- ели и без меры пили вино. Чехов, Без заглавия;
2) в сильной степени, безмерно.
Что гадать? ты влюблена без меры И судьбы своей ты не уйдешь. Н. Некрасов, Гадающей невесте.

... слабой сходимости под действием непрерывных отображений Формулировка теоремы Прохорова о плотности семейства мер Принцип инвариантности (формулировки теорем Донскера , Прохорова , Боровкова , Скорохода ). Формулировка теоремы ... ... сходится , когда xn → x ∈ X В частности , пространство X топологиче -. ски вкладывается в пространство вероятностных мер на X, наделенное слабой . топологией Докажите , что любая вероятностная мера на Rn является слабым пределом ... (вероятностные процессы)
... Интеграл по ортогональной случайной мере ( конечной и -конечной структурной . меры ... (вероятностные процессы)
 ... = (Аь ,An ), Aj = (A^,. ,A^-m )) G Em , j = l,. ,n Теорема 5 верна и для векторного случая (для мер Рт ., заданных на пространствах (Em В этом (векторном ) случае в условии (.а) одновременно переставляются ti ,. , tn и Ai ... ... = E, t G Г), а (ОА , =. = (Ai , , An Li , для А = (Ai ,. , An ) G E™. Доказательство В силу взаимно-однозначного соответствия между мерами на (En , S^iW . и характеристическими функциями условия (А) и (В) леммы 10 равносильны .тому , что при п ^ 2 ... (вероятностные процессы)
... = (Аь ,An ), Aj = (A^,. ,A^-m )) G Em , j = l,. ,n Теорема 5 верна и для векторного случая (для мер Рт ., заданных на пространствах (Em В этом (векторном ) случае в условии (.а) одновременно переставляются ti ,. , tn и Ai ... ... = E, t G Г), а (ОА , =. = (Ai , , An Li , для А = (Ai ,. , An ) G E™. Доказательство В силу взаимно-однозначного соответствия между мерами на (En , S^iW . и характеристическими функциями условия (А) и (В) леммы 10 равносильны .тому , что при п ^ 2 ... (вероятностные процессы)
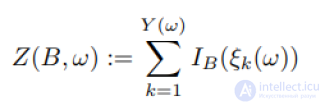 ... меры пуассоновского типа , где. члены семейства PT инвариантны при ограничении на подпространство Пуассоновские случайные меры (S, B), ξ1,. - н о р со значениями в S, Х - конечная мера на (S, B.) Введем случайный процесс Y ∼ P ois (λ(s)),Үи {ξk.} независимыҮ и ξk могут принимать значения ... ... случайный процесс Y ∼ P ois (λ(s)),Үи {ξk.} независимыҮ и ξk могут принимать значения в разных пространствах - пуассоновская случайная мера См ... (вероятностные процессы)
... меры пуассоновского типа , где. члены семейства PT инвариантны при ограничении на подпространство Пуассоновские случайные меры (S, B), ξ1,. - н о р со значениями в S, Х - конечная мера на (S, B.) Введем случайный процесс Y ∼ P ois (λ(s)),Үи {ξk.} независимыҮ и ξk могут принимать значения ... ... случайный процесс Y ∼ P ois (λ(s)),Үи {ξk.} независимыҮ и ξk могут принимать значения в разных пространствах - пуассоновская случайная мера См ... (вероятностные процессы)
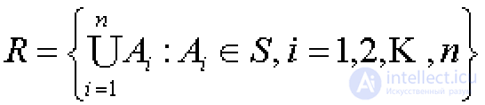 ... m мера , простроенная по теореме 7 на полукольце ячеек . Эта мера порождает внешнюю меру (теорема Мера , порожденная этой внешней . мерой на множествах из Rn называется мерой ... ... , при этом m(D) = VD . Доказательство Доказательство легко вытекает из вложений Ì Ì D.*ÇЕ и вытекающего отсюда неравенства внешних мер m*() £ m*(.) £ m*(D*ÇЕ), а также равенства m*(D*\D =. Теорема Всякое конечное или счетное множество А точек из Rn . измеримо ... (Функциональный анализ)
... m мера , простроенная по теореме 7 на полукольце ячеек . Эта мера порождает внешнюю меру (теорема Мера , порожденная этой внешней . мерой на множествах из Rn называется мерой ... ... , при этом m(D) = VD . Доказательство Доказательство легко вытекает из вложений Ì Ì D.*ÇЕ и вытекающего отсюда неравенства внешних мер m*() £ m*(.) £ m*(D*ÇЕ), а также равенства m*(D*\D =. Теорема Всякое конечное или счетное множество А точек из Rn . измеримо ... (Функциональный анализ)
... фактормножество , 18 фактор-пространство , 110 фактортопология , 19 фундаментальная последовательность , 26 фундаментальность по мере , 76 функция Дирихле , 78 функция множества , 52 функция ограниченной вариации ... (Функциональный анализ)
Комментарии
Оставить комментарий