Лекция
Привет, мой друг, тебе интересно узнать все про приближенное решение нелинейных алгебраических уравнений, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое приближенное решение нелинейных алгебраических уравнений , настоятельно рекомендую прочитать все из категории Численные методы.
Метод деления отрезка пополам (дихотомии)
Метод простой итерации
Метод Ньютона (метод касательных)
Метод хорд
Постановка задачи
Дано нелинейное алгебраическое уравнение
f(x)=0 (1)
Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.
Решить уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней. Геометрическая интерпретация корней уравнения представлена на рис. 1. Корнями уравнения (1) являются точки x1*, x2*, x3*, в которых функция f(x) пересекает ось x.
 Методы решения нелинейного уравнения (1) можно разделить на точные (аналитические) и приближенные (итерационные). В точных методах корень представляется некоторой алгебраической формулой. Например, решение квадратных уравнений, некоторых тригонометрических уравнений и т. д.
Методы решения нелинейного уравнения (1) можно разделить на точные (аналитические) и приближенные (итерационные). В точных методах корень представляется некоторой алгебраической формулой. Например, решение квадратных уравнений, некоторых тригонометрических уравнений и т. д.
В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности {xn}, такой, что 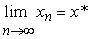 . По определению предела, для любого (сколь угодно малого) ε, найдется такое N, что при n>N, |xn – x*|< ε. Члены этой последовательности xn называются последовательными приближениями к решению, или итерациями. Наперед заданное число ε называют точностью метода, а N – это количество итераций, которое необходимо выполнить, чтобы получить решение с точностью ε.
. По определению предела, для любого (сколь угодно малого) ε, найдется такое N, что при n>N, |xn – x*|< ε. Члены этой последовательности xn называются последовательными приближениями к решению, или итерациями. Наперед заданное число ε называют точностью метода, а N – это количество итераций, которое необходимо выполнить, чтобы получить решение с точностью ε.
Существует различные методы нахождения приближенного решения, т.е. способы построения последовательности итераций {xn}, однако все они имеют общие этапы, изображенные на рисунке.

Наиболее часто используется следующий критерий остановки итерационного процесса: |xn+1–xn|<ε, т.е. разница между соседними итерациями становится малой. Также для окончания итерационного процесса используется условие |f(xn)|<ε , где f(xn) – невязка метода.
Прежде чем использовать приближенный метод, уравнение надо исследовать его на наличие корней и уточнить, где эти корни находятся, т.е. найти интервалы изоляции корней. Интервалом изоляциикорня называется отрезок, на котором корень уравнения существует и единственен.
Необходимое условие существования корня уравнения на отрезке [a,b]: Пусть f(x) непрерывна и f(a)f(b)<0 (т.е., на концах интервала функция имеет разные знаки). Тогда внутри отрезка [a, b] существует хотя бы один корень уравнения f(x)=0.
Достаточное условие единственности корня на отрезке [a,b]:
Корень будет единственным, если f(a)f(b)<0 и f /(x) не меняет знак на отрезке [a, b], т.е. f(x) – монотонная функция, в этом случае отрезок [a,b] будет интервалом изоляции.
Если корней несколько, то для каждого нужно найти интервал изоляции.
Существуют различные способы исследования функции: аналитический, табличный, графический.
Аналитический способ состоит в нахождении экстремумов функции f(x), исследование ее поведения при  и нахождение участков возрастания и убывания функции.
и нахождение участков возрастания и убывания функции.
Графический способ – это построение графика функции f(x) и определение числа корней по количеству пересечений графика с осью x.
Табличный способ – это построение таблицы, состоящей из столбца аргумента x и столбца значений функции f(x). О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.
Пример.
Решить уравнение x3‑ 6x2+3x+11=0, т.е. f(x)= x3‑ 6x2+3x+11.
Найдем производную f/(x)=3x2-12x+3.
Найдем нули производной f/(x)=3x2-12x+3=0; D=144-4*3*3=108;
X1=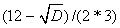 = 0.268;
= 0.268;
X2=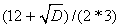 = 3.732;
= 3.732;
Так как f/(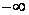 )>0, то f/(x)>0 при
)>0, то f/(x)>0 при 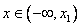 , f/(x)<0 при
, f/(x)<0 при 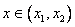 и f/(x)>0 при
и f/(x)>0 при 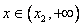 . Кроме того, f(
. Кроме того, f(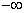 )=
)=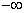 <0, f(
<0, f(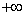 )=
)=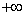 >0. Следовательно, на интервале
>0. Следовательно, на интервале возрастает от
возрастает от 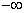 до f(x1)= 3x12-12x1+3=11.39; на интервале
до f(x1)= 3x12-12x1+3=11.39; на интервале 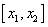 - убывает до f(x2)= 3x22-12x2+3=-9.39 и на интервале
- убывает до f(x2)= 3x22-12x2+3=-9.39 и на интервале 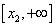 возрастает до
возрастает до 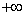 , т.е. уравнение имеет три корня.
, т.е. уравнение имеет три корня.
Найдем интервалы изоляции для каждого из корней.
Рассмотрим для первого корня отрезок [-2, -1]:
f(-2)= -27<0, f(-1)= 1>0, f/(x)>0 при 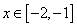 т.е. этот отрезок является интервалом изоляции корня.
т.е. этот отрезок является интервалом изоляции корня.
Рассмотрим для второго корня отрезок [1, 3]:
f(1)= 9>0, f(3)= -7<0, f/(x)<0 при 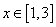 т.е. этот отрезок является интервалом изоляции корня.
т.е. этот отрезок является интервалом изоляции корня.
Рассмотрим для третьего корня отрезок [4, 5]:
f(4)= -9<0, f(5)=1>0, f/(x)>0 при 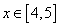 т.е. этот отрезок является интервалом изоляции корня.
т.е. этот отрезок является интервалом изоляции корня.
Табличный способ:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
f(x) |
-79 |
-27 |
1 |
11 |
9 |
1 |
-7 |
-9 |
1 |
29 |
81 |
Графический способ
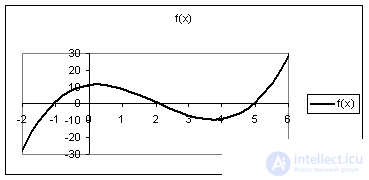
Приближенные (Итерационные) методы.
Пусть интервалы изоляции корней известны. Познакомимся с несколькими итерационными методами, позволяющими найти корень на известном интервале изоляции [a, b].
Идея метода:
Найдем середину отрезка [a, b]: c=(a+b)/2. Корень остался на одной из частей: [a, c] или [c, b]. Если f(a) * f(с)<0, то корень попал на отрезок [a, c], тогда деление отрезка можно повторить, приняв в качестве нового правого конца точку c, т.е. b=c. В противном случае корень попал на половину [c, b], и необходимо изменить значение левого конца отрезка: a=c. Поскольку корень всегда заключен внутри отрезка, итерационный процесс можно останавливать, если длина отрезка станет меньше заданной точности: |b – a|< ε Найдем первый корень уравнения f(x)=x3 - 6x2+3x+11=0 с точностью 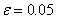
Вычисления оформляются в виде таблицы
|
k |
a |
b |
c |
f(a) |
f(c) |
|b-a| |
|
0 |
-2 |
-1 |
-1.5 |
-27 |
-10.375 |
1 |
|
1 |
-1.5 |
-1 |
-1.25 |
-10.375 |
-4.07813 |
0.5 |
|
2 |
-1.25 |
-1 |
-1.125 |
-4.07813 |
-1.39258 |
0.25 |
|
3 |
-1.125 |
-1 |
-1.0625 |
-1.39258 |
-0.1604 |
0.125 |
|
4 |
-1.0625 |
-1 |
-1.03125 |
-0.1604 |
0.42868 |
0.0625 |
|
5 |
-1.0625 |
-1.03125 |
-1.04688 |
-0.1604 |
0.136372 |
0.03125 |
|
6 |
.......... |
|||||
|
7 |
||||||
|
8 |
||||||
|
9 |
||||||
|
10 |
-1.05469 |
-1.05371 |
-1.0542 |
-0.01146 |
-0.00218 |
0.000977 |
где a0 , b0 - начальные границы интервала изоляции корня; 
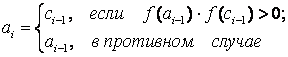
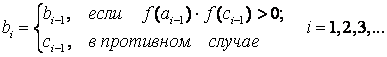
В результате расчета приближенное значение первого корня: 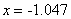 при точности
при точности 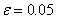 и х=-1.0542 при точности
и х=-1.0542 при точности 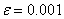 .
.
Графическая иллюстрация метода:
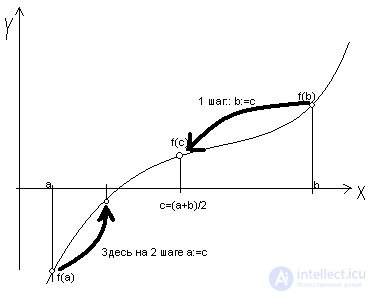
Этот пример в Excel: dich.xls (20 Кб)
С помощью эквивалентных преобразований приведем исходное уравнение f(x) к виду, удобному для применения метода простой итерации: x=φ(x). Выберем начальное приближение x0∈[a, b]. Следующие итерации находим по формуле: xk+1=φ(xk), т.е. x1=φ(x0), x2=φ(x1) и т.д.. Об этом говорит сайт https://intellect.icu . Итерационный процесс заканчивается, если |xk+1–xk|<ε. Представить исходное уравнение в эквивалентном виде x=φ(x) можно бесконечным числом способов. Из всевозможных таких представлений выбирают тот, который дает сходящуюся к корню последовательность вычислений. Очевидно, что  .
.
Достаточное условие сходимости: пусть φ(x) имеет производную на отрезке [a,b],  и
и 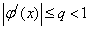 для всех x из отрезка [a,b], тогда итерационный процесс сходится к корню уравнения т.е.
для всех x из отрезка [a,b], тогда итерационный процесс сходится к корню уравнения т.е. 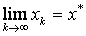 .
.
Доказательство следует из следующих оценок:
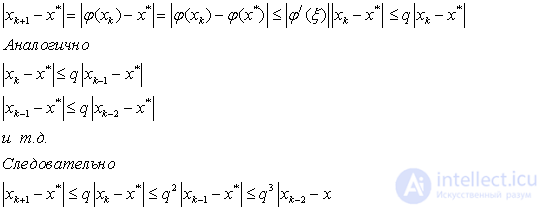
Первое неравенство следует из теоремы Лагранжа о среднем и того, что  .
.
Остальные по инерции.
Так как 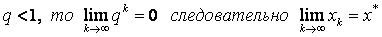 .
.
Геометрический смысл метода простой итерации.
|
|
|
|
|
|
|
Сходящийся метод простой итерации |
|
|
|
|
|
|
|
|
Расходящийся метод простой итерации |
|
В качестве начального приближения обычно берут середину отрезка [a,b]: 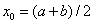 .
.
На практике часто в качестве 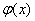 берут функцию
берут функцию 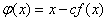 , где с – некоторая постоянная. Постоянную c выбирают таким образом, чтобы
, где с – некоторая постоянная. Постоянную c выбирают таким образом, чтобы 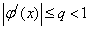 для всех x∈[a, b].
для всех x∈[a, b].
При таком выборе функции 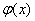 метод простой итерации называют методом релаксации.
метод простой итерации называют методом релаксации.
Получим условия на выбор с:
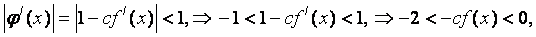
Таким образом, если f/(x)<0, то 2/f/(x)<c<0. Если же f/(x)>0, то 2/f/(x)>c>0.
Видно, что знак у с совпадает со знаком f/(x). Часто с берут в виде: 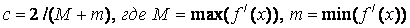 .
.
Убедимся, что такое c удовлетворяет условию сходимости:
Пусть f/(x)>0. Тогда M>0 и m>0 -> c>0 и 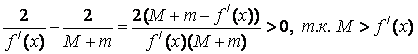 . Следовательно, 2/f/(x)>c>0.
. Следовательно, 2/f/(x)>c>0.
Пусть f/(x)<0. Тогда M<0 и m<0-> c<0 и
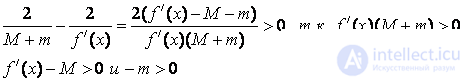
Следовательно, 2/f/(x)<c<0.
Найдем, второй корень нашего исходного уравнения x3‑ 6x2+3x+11=0, который лежит на интервале [1, 3] с точностью 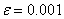 .
.
Сначала найдем функцию 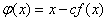 . В нашем случае f(x)= x3‑ 6x2+3x+11.
. В нашем случае f(x)= x3‑ 6x2+3x+11.
Для нахождения c необходимо найти максимальное и минимальное значения f/(x) на отрезке [1, 3]. Для этого необходимо найти значения f/(x) на концах интервала и в точках, где f//(x)=0, т.е. в точках экстремума, если такие точки для рассматриваемого интервала существуют. И выбрать среди этих значений f/(x) максимальное и минимальное значения.
f/(1)=3x2-12x+3=-6, f/(3)=-6, f//(x)=6x-12=0 при x=2 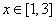 , f/(2)=-8.
, f/(2)=-8.
Следовательно, 
Таким образом, 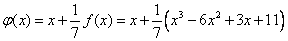 .
.
Вычисления оформим в виде таблицы:
|
k |
x |
|xk+1-xk| |
|f(xk)| |
|
0 |
2 |
- |
1 |
|
1 |
2.142857 |
0.142857 |
0.282799 |
|
2 |
2.102457 |
0.0404 |
0.07896 |
|
3 |
2.113737 |
0.01128 |
0.022164 |
|
4 |
2.110571 |
0.003166 |
0.006213 |
|
5 |
2.111459 |
0.000888 |
0.001742 |
|
6 |
2.11121 |
0.000249 |
0.000489 |
Здесь x0=(1+3)/2=2, 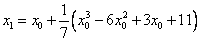 ,
, 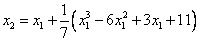 и т.д.
и т.д.
Условием окончания итерационного процесса является условие: |xk+1–xk|<ε или |f(xk)|<ε.
Напомним, что мы решаем уравнение f(x)=0.
Метод определяется формулой


Геометрическая интерпретация такова: участок кривой y=f(x) при 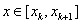 , если
, если 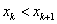 , или
, или 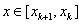 , если
, если 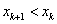 , заменяется отрезком касательной, проведенной из точки xk.
, заменяется отрезком касательной, проведенной из точки xk.
Уравнение касательной имеет вид 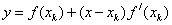 . Найдем точку пересечения, которую обозначим xk+1, касательной с осью y=0:
. Найдем точку пересечения, которую обозначим xk+1, касательной с осью y=0:  .
.
Откуда 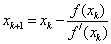 .
.
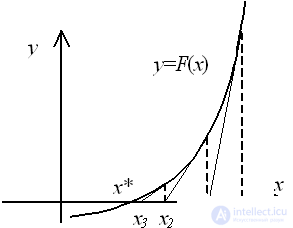
Можно показать, что |xk+1– x*| < q * |xk – x*|2, т.е. метод сходится со вторым порядком.
Метод Ньютона можно трактовать как метод простой итерации при 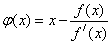 .
.
Замечание. Если известен интервал изоляции корня уравнения, в котором f//(x) не меняет знак, то в качестве начального приближения берут тот конец интервала изоляции, для которого знаки f(x) и f//(x) совпадают.
Найдем, третий корень методом Ньютона нашего исходного уравнения x3‑ 6x2+3x+11=0, который лежит на интервале [4, 5] с точностью 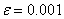 . Сначала убедимся, что f//(x) не меняет знака на этом отрезке.
. Сначала убедимся, что f//(x) не меняет знака на этом отрезке.
f//(x)=6x-12. f//(x)>0 при x>2, т.е. f//(x)>0 на интервале [4,5]. Так как f(5)=1>0, то x0=5.
Вычисления оформим в виде таблицы:
|
k |
xk |
|xk+1-xk| |
f(xk) |
f/(xk) |
|
0 |
5 |
- |
1 |
18 |
|
1 |
4.944444 |
0.055556 |
0.027606 |
17.00926 |
|
2 |
4.942821 |
0.001623 |
2.33E-05 |
16.98059 |
|
3 |
4.94282 |
1.37E-06 |
1.66E-11 |
16.98057 |
Здесь f(xk)=xk3‑ 6xk2+3xk+11, f/(xk)=3xk-12xk+3, 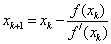 .
.
В качестве корня можно взять значение: x=4.943. Видно, что процесс сошелся уже на второй итерации.
Для сравнения найдем первый корень нашего уравнения x3‑ 6x2+3x+11=0 на отрезке [-2,-1] методом Ньютона:
Так как f//(x)=6x-12, то f//(x)<0 на интервале [-2,-1], а так как f(-2)=-27>0, то x0=-2.
|
k |
xk |
|xk+1-xk| |
f(xk) |
f/(xk) |
|
0 |
-2 |
-27 |
39 |
|
|
1 |
-1.30769 |
0.692308 |
-5.41966 |
23.82249 |
|
2 |
-1.08019 |
0.227502 |
-0.50182 |
19.46272 |
|
3 |
-1.05441 |
0.025783 |
-0.00613 |
18.9882 |
|
4 |
-1.05408 |
0.000323 |
-9.5E-07 |
18.98229 |
|
5 |
-1.05408 |
5.02E-08 |
-2.3E-14 |
18.98229 |
Напомним, что методом дихотомии мы достигли данной точности 0.001 на 10-ой итерации.
Вычислим второй корень нашего уравнения на отрезке [1,3]. Заметим, что f//(x)=6x-12 меняет знак на отрезке при х=2. Уменьшим интервал изоляции так, чтобы f//(x) не меняла знака. Рассмотрим интервал [2.1; 3]. f//(2.1)=6*2.1-12=0.6>0 b f(2.1)=0.101>0. Следовательно, x0=2.1.
|
k |
xk |
|xk+1-xk| |
f(xk) |
f/(xk) |
|
0 |
2.1 |
0.101 |
-8.97 |
|
|
1 |
2.11126 |
0.01126 |
3.95E-05 |
-8.96286 |
|
2 |
2.111264 |
4.4E-06 |
6.47E-12 |
-8.96286 |
|
3 |
2.111264 |
7.22E-13 |
0 |
-8.96286 |
Если сравнивать с методом простой итерации, то значение этого корня мы получили за две итерации вместо шести.
Эти примеры показывают, что метод Ньютона является более быстросходящимся. Но для его использования необходимо брать начальное приближение достаточно близким к корню.
Упрощенный метод Ньютона. Эта модификация метода Ньютона используется, если производная f /(x) представляет собой сложную функцию, и для ее вычисления на каждой итерации используется много времени. Зададим x0 – начальное приближение и вычислим производную z=f /(x0). На следующих итерациях используется вычисленное значение производной:  . Это упрощение несколько замедляет процесс сходимости к решению, однако сокращает время каждого итерационного цикла.
. Это упрощение несколько замедляет процесс сходимости к решению, однако сокращает время каждого итерационного цикла.
В этом методе кривая f(x) заменяется прямой линией – хордой, стягивающей точки (a, f(a)) и (b, f(b)). В зависимости от знака выражения f(a) f //(a) метод хорд имеет два варианта, изображенных на рис. 2 а, б.
|
|
|
|
Рис. 2. Метод хорд для F(a)F //(a)>0 (а) и F(a)F //(a)<0 (б) |
|
Пусть f(a)f //(a)>0 (рис. 2 а). Тогда x0=b, точка a будет оставаться неподвижной. Следующее приближение x1 находим как точку пересечения хорды, соединяющей точки (a, f(a)) и (x0, f(x0)) с осью x. Уравнение хорды:  . Тогда точка пересечения хорды с осью x:
. Тогда точка пересечения хорды с осью x: 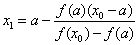 .
.
Пусть теперь f(a)f //(a)<0 (рис. 2). Тогда x0=a, точка b неподвижна. Проведем хорду, соединяющую точки (b, f(b)) и (x0, f(x0)):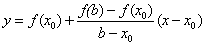 . Вычисляем точку пересечения хорды с осью x:
. Вычисляем точку пересечения хорды с осью x:  .
.
На следующей итерации в качестве x0 надо взять вычисленное значение x1.
Таким образом, имеем следующую последовательность вычислений:
Если f(a) f //(a)>0, то x0=b и 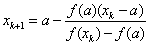 .
.
Если же f(a) f //(a)<0, то x0=a и  .
.
Окончание итерационного цикла в этом методе происходит по условию малости невязки уравнения: |f(x1)| < ε или 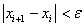 .
.
Задание. Найти первый и третий корень уравнения x3‑ 6x2+3x+11=0 методом хорд.
Для первого корня a=-2, b=-1. 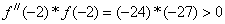 , тогда расчет ведется по первым формулам: x0=b и
, тогда расчет ведется по первым формулам: x0=b и 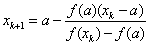 .
.
|
k |
xk |
|xk+1-xk| |
f(xk) |
|
0 |
-1 |
1 |
|
|
1 |
-1.03571 |
0.035714 |
0.345618 |
|
2 |
-1.0479 |
0.012187 |
0.117007 |
|
3 |
-1.05201 |
0.004108 |
0.039334 |
|
4 |
-1.05339 |
0.001379 |
0.013192 |
|
5 |
-1.05385 |
0.000462 |
0.004421 |
Для последнего корня: a=4, b=5, 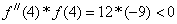 , тогда расчет ведется по вторым формулам: x0=a и
, тогда расчет ведется по вторым формулам: x0=a и  .
.
|
k |
xk |
|xk+1-xk| |
f(xk) |
|
0 |
4 |
-9 |
|
|
1 |
4.9 |
0.9 |
-0.711 |
|
2 |
4.941555 |
0.041555 |
-0.02147 |
|
3 |
4.942783 |
0.001229 |
-0.00062 |
|
4 |
4.942819 |
3.57E-05 |
-1.8E-05 |
Я хотел бы услышать твое мнение про приближенное решение нелинейных алгебраических уравнений Надеюсь, что теперь ты понял что такое приближенное решение нелинейных алгебраических уравнений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Численные методы
Комментарии
Оставить комментарий
Численные методы
Термины: Численные методы