7. Сети, являющиеся развитием модели Хопфилда кратко

Привет, сегодня поговорим про сети являющиеся развитием модели хопфилда, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое сети являющиеся развитием модели хопфилда , настоятельно рекомендую прочитать все из категории Интеллектуальные информационные системы.

Сеть Хэмминга

Когда нет необходимости, чтобы сеть в явном виде выдавала образец, то есть достаточно, скажем, получать номер образца, ассоциативную память успешно реализует сеть Хэмминга. Данная сеть характеризуется, по сравнению с сетью Хопфилда, меньшими затратами на память и объемом вычислений, что становится очевидным из ее структуры.

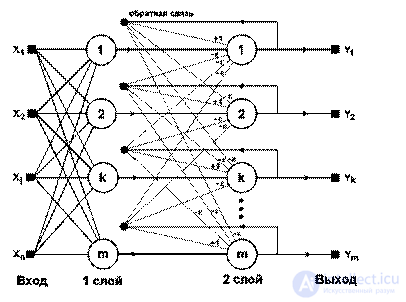
Рисунок 7.1 – Сеть Хэмминга.

Сеть состоит из двух слоев. Первый и второй слои имеют по m нейронов, где m – число образцов. Нейроны первого слоя имеют по n синапсов, соединенных со входами сети (образующими фиктивный нулевой слой). Нейроны второго слоя связаны между собой ингибиторными (отрицательными обратными) синаптическими связями. Единственный синапс с положительной обратной связью для каждого нейрона соединен с его же аксоном.

Идея работы сети состоит в нахождении расстояния Хэмминга от тестируемого образа до всех образцов. Расстоянием Хэмминга называется число отличающихся битов в двух бинарных векторах. Сеть должна выбрать образец с минимальным расстоянием Хэмминга до неизвестного входного сигнала, в результате чего будет активизирован только один выход сети, соответствующий этому образцу.

На стадии инициализации весовым коэффициентам первого слоя и порогу активационной функции присваиваются следующие значения:

, i=1...n, k=1...m;

w_0k = n/2, k = 1...m.

где x_i^k – i-ый элемент k-ого образца.

Весовые коэффициенты тормозящих синапсов w_ij, i≠j, во втором слое принимают равными некоторой величине 0 < e < 1/m. Синапс нейрона, связанный с его же аксоном имеет вес w_ii = 1.

Алгоритм функционирования сети Хэмминга следующий:

1. На входы сети подается неизвестный вектор X = {xi:i=1...n}, исходя из которого рассчитываются состояния нейронов первого слоя:

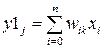, j=1...m.

После этого полученными значениями инициализируются значения аксонов второго слоя: y2_j=y1_j, j=1...m.

2. Вычислить новые состояния нейронов второго слоя:

3. Об этом говорит сайт https://intellect.icu . Проверить, изменились ли выходы нейронов второго слоя за последнюю итерацию. Если да – перейди к шагу 2. Иначе – конец.

Из оценки алгоритма видно, что роль первого слоя весьма условна: воспользовавшись один раз на шаге 1 значениями его весовых коэффициентов, сеть больше не обращается к нему, поэтому первый слой может быть вообще исключен из сети и заменен на матрицу весовых коэффициентов.

Двунаправленная ассоциативная память

Ассоциативная память, реализуемая сетью Хопфилда, является автоассоциативной: образ, хранящийся в сети, может быть восстановлен по искаженному входу (этому же вектору), но не ассоциирован с произвольным другим образом. В 1980 – 83 гг. С. Гроссберг опубликовал серию работ по так называемой двунаправленной ассоциативной памяти.

Рисунок 7.2 – Сеть двунаправленной ассоциативной памяти.

Двунаправленная ассоциативная память (ДАП) фактически представляет собой объединение двух слоев сети Хопфилда. В этом случае происходит гетерассоциация двух векторов A и B. Ассоциируемые образы A и B кодируются двоичными векторами длиной n1 и n2 соответственно. Затем веса сети ДАП задаются по формуле:

Для восстановления ассоциации, входной вектор A подается на входы слоя 1 и обрабатывается матрицей весов W, в результате на выходе слоя должен формироваться вектор B:

B = f(AW),

где f() – передаточная функция (6.3).

Входной вектор слоя 2 B обрабатывается матрицей весов W^T, в результате на выходе слоя 2 и формируется вектор A, который затем передается на входы слоя 1:

A = f(BW^T),

где W^T – транспозиция матрицы W.

Цикл повторяются до тех пор, пока сеть ДАП не стабилизируется, то есть ни вектор A, ни вектор B не изменятся от итерации к итерации. В результате значение вектора B будет искомой ассоциацией вектору A.

Емкость памяти ДАП, представленной сетью с N нейронами в меньшем слое, можно оценить следующей величиной:

L < N/(2log₂N).

Емкость ДАП невысока, для N = 1024 нейронов сеть будет в состоянии запомнить 50 образов.

Машина Больцмана. Стохастическая модель нейрона

Правило обучения Больцмана, названное так в честь Людвига Больцмана, представляет собой стохастический алгоритм обучения, основанный на идеях стохастической механики. Нейронная сеть, созданная на основе обучения Больцмана, получила название машины Больцмана. В своей базовой форме машина Больцмана является сетью Хопфилда, использующей стохастическую модель нейронов.

В машине Больцмана нейроны могут находиться во включенном (соответствующем значению +1) или выключенном (-1) состоянии. Машина характеризуется функцией энергии,значение которой определяется конкретными состояниями отдельных нейронов, составляющих эту машину:

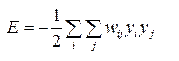
Работа машины заключается в выполнении следующих действий:

– случайном выборе некоторого нейрона j на определенном шаге процесса обучения;

– переводе этого нейрона из состояния хj в состояние -xj с вероятностью:

Где ΔE_J – изменение энергии машины, вызванное сменой состояния нейрона j: ;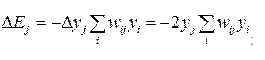

T – псевдотемпература, котораяне описывает физическую температуру естественной или искусственной сети, а является параметром синаптического шума. Чем меньше синаптический шум, тем больше стохастический нейрон приближается к детерминированному. При многократном применении этого правила машина достигает термального равновесия.

Нейроны машины Больцмана можно разбить на две функциональные группы. Видимые нейроны реализуют интерфейс между сетью и средой ее функционирования, а скрытые работают независимо от внешней среды. Рассмотрим два режима функционирования такой сети.

• Скованное состояние (фаза фиксации), в котором все видимые нейроны находятся в состояниях, предопределенных внешней средой (т.е. заданы вход и целевой ассоциированный выход).

• Свободное состояние (фаза свободного выполнения), в котором фиксируется только входной вектор, а сеть работает, пока не стабилизируются значения выхода.

В течение обеих фаз собирается статистика, которая используется для изменения весов связей согласно правилу обучения Больцмана:

,

где – корреляциямежду состояниями нейронов j и i в скованном состоянии;

–– в свободном состоянии.

Вау!! 😲 Ты еще не читал? Это зря!

• сеть хопфилда , модели нейронных сетей , ассоциативная память ,

В общем, мой друг ты одолел чтение этой статьи об сети являющиеся развитием модели хопфилда. Работы впереди у тебя будет много. Смело пиши комментарии, развивайся и счастье окажется в твоих руках. Надеюсь, что теперь ты понял что такое сети являющиеся развитием модели хопфилда и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Интеллектуальные информационные системы

Из статьи мы узнали кратко, но содержательно про сети являющиеся развитием модели хопфилда