Лекция
Привет, сегодня поговорим про сети на основе радиально-базисных функций, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое сети на основе радиально-базисных функций, сети каскадной корреляции , настоятельно рекомендую прочитать все из категории Интеллектуальные информационные системы.
Основная идея сетей на основе радиальных базисных функций (RBF) состоит в нелинейном преобразовании входных данных в пространстве более высокой размерности. Теоретическую основу такого подхода составляет теорема Ковера о разделимости образов:
Нелинейное преобразование сложной задачи классификации образов в пространство более высокой размерности повышает вероятность линейной разделимости образов.
RBF-сети берут свое начало от теории точного приближения функций, предложенной Пауэлом в 1987 г. Пусть задан набор из N входных векторов xn с соответствующими выходами yn. Задача точного приближения функций – найти такую функцию y, чтобы y(xn) = yn, n = 1,...,N. Для этого Пауэл предложил использовать набор базисных функций вида 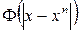 , тогда получаем обобщенный полином вида:
, тогда получаем обобщенный полином вида:
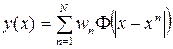 (5.1)
(5.1)
Здесь wn – свободно настраиваемые параметры.
Обычно в качестве базисной используют экспоненциальную функцию 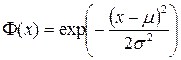 , также называемую функцией Гаусса, где μ и σ – регулирующие параметры, называемые соответственно центром и шириной окна функции.
, также называемую функцией Гаусса, где μ и σ – регулирующие параметры, называемые соответственно центром и шириной окна функции.
Также в качестве базисных функций используются мультиквадратичная и обратная мультиквадратичная функции, соответственно:
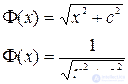
Привмер аппроксимации неизвестной функции y(x) с помощью функций Гаусса показан на рисунке 5.1. На этом рисунке красная кривая представлена суммой синих гауссоид, ясно что для некоторой точки x основной вклад дают лишь несколько гауссоид, центры которых близки к этой точке. Поэтому такая аппроксимация называется локальной.
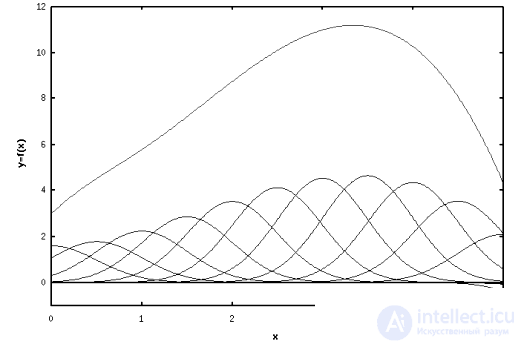
Рисунок 5.1 – Локальная аппроксимация функции.
Аппроксимация функции по формуле (5.1) дает плохие результаты для зашумленных данных, поэтому в 1988 г. Д. Брумхеад и Д. Лоув предложили модель RBF-сети. Сеть с радиальными базисными функциями (RBF-сеть) в наиболее простой форме представляет собой сеть с тремя слоями: входным слоем, одним скрытым слоем и выходным слоем. Скрытый слой выполняет нелинейное преобразование входного пространства в скрытое. Об этом говорит сайт https://intellect.icu . В большинстве случаев, но не всегда, количество нейронов в скрытом слое больше размерности входного пространства. Выходной слой осуществляет линейное преобразование выхода скрытого слоя, т.е. в его нейронах всегда используется линейная функция активации.
С каждым скрытым элементом связывается радиальная базисная функция Φ(x). Каждая из этих функций берет комбинированный ввод и порождает значение активности, подаваемое на выход.
Связи элемента скрытого слоя определяют центр радиальной функции для данного скрытого элемента. В RBF-сети активизация нейронов задается дистанцией (евклидовой нормой) между весовым вектором и заданным в процессе обучения образцом:
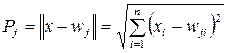 (5.2)
(5.2)
Весовой вектор wj служит центром радиально-базисной функции, соответствующей нейрону с номером j. Поэтому обозначим его как μj.
Правила задания и обучение RBF-сети
1. Число M базисных функций выбирается много меньше числа обучающих данных: M<<N. В качестве базисной функции здесь так же берут экспоненциальную функцию:
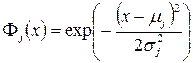 (5.3)
(5.3)
2. Центры базисных функций μj не опираются на точки входных данных, т.е. не совпадают ни с одним из входных векторов. Определение центров функций становится частью процесса обучения.
3. Для каждой из M базисных функций задается своя ширина окна σj, которая также определяется в процессе обучения RBF-сети. Как правило, значение σj делают чуть большим расстояния между центрами соответствующих базисных функций μj.
4. В сумму (5.1) добавляется константа wk0 – порог нейрона и формальный скрытый нейрон Φ0(x)=0. В итоге RBF-сеть будет описываться формулой:
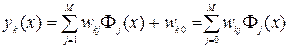 (5.4)
(5.4)
Обучение RBF-сети происходит быстро и носит элементы как обучения «с учителем», так и «без учителя».
Имеем обучающий набор: множество входов {xn} и соответствующих выходов {dn}. На первом этапе определяются параметры базисных функций: μj, σj. Причем, используются только входные векторы {xn}, т.е. обучение происходит по схеме «без учителя».
Для определения σj используется алгоритм «ближайшего соседа», который заключается в поиске разбиения множества {xn} на M несмежных подмножеств Sj. Таким образом, необходимо минимизировать функцию:
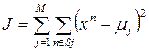 , где
, где 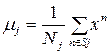 – центры функций.
– центры функций.
На втором этапе фиксируются базисные функции, т.е. параметры μj, σj постоянны. На данном этапе RBF-сеть эквивалентна однослойной нейронной сети. Затем обучение происходит по правилу обучения с учителем. Выражение энергии ошибки:
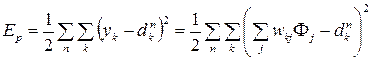
Так как E является квадратической функцией от весов w, то минимум E может быть найден решением системы линейных уравнений:
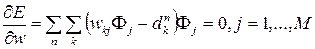
Решение такой системы находится быстро, и в этом одно из преимуществ RBF-сети над многослойным персептроном.
Среди недостатков RBF-сети по сравнению с MLP, обычно отмечают следующие: требуется больше обучающих примеров, а круг решаемых задач ограничен аппроксимацией и классификацией.
Построение нейронных сетей по алгоритму каскадной корреляции начинается с персептрона. Алгоритм можно разбить на две части: обучение нейронов персептрона и создание новых нейронов.
На начальном этапе, когда обучается персептрон, после того, как в течение заданного числа эпох не происходит существенного уменьшения ошибки, принимается решение о создании нового нейрона.
Во второй части алгоритма новый нейрон-кандидат добавляется к существующей сети, причем его входы соединяются со всеми входами сети и выходами уже добавленных прежде нейронов-кандидатов. Входные веса кандидата настраиваются особым образом так, чтобы максимально уменьшить ошибку на выходе полученной сети. На рисунке 5.2 показана сеть с двумя добавленными нейронами.
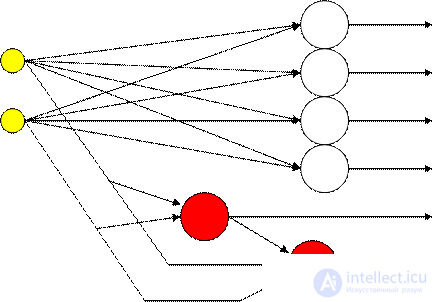
Рисунок 5.2 – Сеть каскадной корреляции.
Метод получил такое название потому, что для настройки весов нейрона-кандидата используется сумма корреляций его выхода со значениями уже имеющихся нейронов:
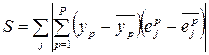
где yp – выход нейрона-кандидата;
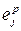 – ошибка выходного нейрона j для образца p;
– ошибка выходного нейрона j для образца p;
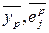 – усредненные по выборке значения соответствующих величин.
– усредненные по выборке значения соответствующих величин.
Цель обучения – максимум функционала S. Для этого вычисляются его частные производные по весам нейрона-кандидата:

где λj – знак корреляции (+ или -) между yp и 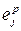 ;
;
I – значение выхода нейрона, добавленного на предыдущем шаге.
В общем, мой друг ты одолел чтение этой статьи об сети на основе радиально-базисных функций. Работы впереди у тебя будет много. Смело пиши комментарии, развивайся и счастье окажется в твоих руках. Надеюсь, что теперь ты понял что такое сети на основе радиально-базисных функций, сети каскадной корреляции и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Интеллектуальные информационные системы
Из статьи мы узнали кратко, но содержательно про сети на основе радиально-базисных функций
Комментарии
Оставить комментарий
Интеллектуальные информационные системы
Термины: Интеллектуальные информационные системы