Привет, сегодня поговорим про сети типа персептрон задача классификации образов обучение с учителем, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое сети типа персептрон задача классификации образов обучение с учителем , настоятельно рекомендую прочитать все из категории Интеллектуальные информационные системы.

Ф. Розенблатт предложил использовать персептрон для задач классификации. Многие приложения можно интерпретировать, как проблемы классификации. Например, оптическое распознавании символов. Отсканированные символы ассоциируются с соответствующими им классами. Имеется немало вариантов изображения буквы "Н" даже для одного конкретного шрифта – символ может оказаться, например, смазанным, – но все эти изображения должны принадлежать классу "Н".

Когда известно, к какому классу относится каждый из учебных примеров, можно использовать стратегию обучения с учителем. Задачей для сети является ее обучение тому, как сопоставить предъявляемый сети образец с контрольным целевым образцом, представляющим нужный класс. Иными словами, знания об окружающей среде представляются нейронной сети в виде пар "вход-выход". Например, сети можно предъявить изображение буквы "Н" и обучить сеть тому, что при этом соответствующий "Н" выходной элемент должен быть включен, а выходные элементы, соответствующие другим буквам – выключены. В этом случае входной образец может быть набором значений, характеризующих пиксели изображения в оттенках серого, а целевой выходной образец – вектором, значения всех координат которого должны быть равными 0, за исключением координаты, соответствующей классу "Н", значение которой должно быть равным.

На рисунке 3.1 показана блочная диаграмма, иллюстриру­ющая эту форму обучения. Предположим, что учителю и обучаемой сети подается обучающий вектор из окружающей среды. На основе встроенных знаний учитель может сформировать и передать обучаемой ней­ронной сети желаемый отклик, соответствующий данному входному вектору. Параметры сети корректируются с учетом обучающего век­тора и сигнала ошибки. Сигнал ошибки – это разность между желаемым сигналом и текущим откликом нейронной сети. После окончания обучения учителя можно отключить и позволить нейронной сети работать со средой самостоятельно.

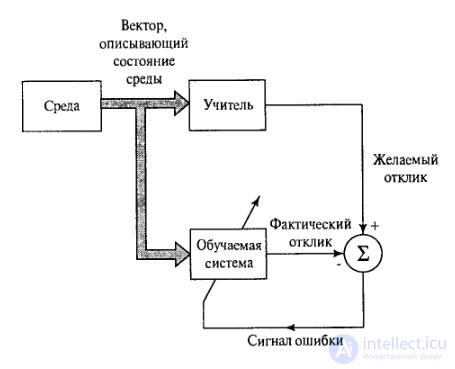
Рисунок 3.1 – Концепция обучения ИНС с учителем.

Алгоритм обучения перцептрона включает следующие шаги:

· Системе предъявляется эталонный образ.

· Если результат распознавания совпадает с заданным, весовые коэффициенты связей не изменяются.

· Если ИНС неправильно распознает результат, то весовым коэффициентам дается приращение в сторону повышения качества распознавания.

Дельта-правило Видроу-Хоффа

В необученной сети связям присвоены случайно выбранные небольшие по значению веса. Разность между известным значением результата и реакцией сети соответствует величине ошибки, которая может использоваться для корректировки весов межнейронных связей. Корректировка заключается в небольшом (обычно менее 1%) увеличении синаптического веса тех связей, которые усиливают правильные реакции, и уменьшении тех, которые способствуют ошибочным.

Введем следующие обозначения:

X – входной вектор из внешней среды;

Y – фактический отклик персептрона;

D – desired output – желаемый отклик персептрона.

Сигнал ошибки инициализирует процедуру их изменения, которая направлена на приближение фактического отклика к желаемому. Если персептрон содержит k нейронов, то векторы в выражении Y и D имеют размерность k, и каждая координата соответствует одному нейрону. В процессе обучения осуществляется минимизация энергии полной ошибки, т.е. суммы ошибок по всем образцам, представленным сети на этапе обучения:

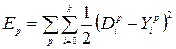 (3.1)

Где р – номер образца,

k – размерность векторов Y и D.

Среднеквадратическая энергия ошибки – энергия ошибки в расчете на один пример:

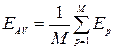 (3.2)

Где M – количество обучающих примеров.

Время, в течение которого через сеть прогоняются все примеры из обучающей выборки, назывется эпохой.

Минимизация функции осуществляется по дельта-правилу, или правилу Видроу-Хоффа. Об этом говорит сайт https://intellect.icu . Обозначим w_ji(n) текущее значение синаптического веса w_ji нейрона i, соответствующего входу x_j на шаге обучения n. В соответствии с дельта-правилом, изменение синаптического веса задается выражением:

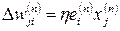 (3.3)

Где η – положительная константа, влияющая на скорость обучения.

Данное правило легко выводится в случае линейной передаточной функции нейронов. Уравнение полной ошибки задает многомерную поверхность. В процессе обучения сеть изменяет весовые коэффициенты так, что осуществляется градиентный спуск по поверхности ошибок. Градиент поверхности ошибок по весовым коэффициентам выражается следующим образом:

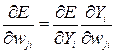 (3.4)

Так как:

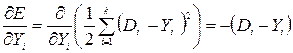; (3.5)

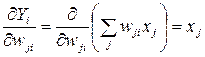. (3.6)

Обозначив 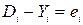, получим выражение градиента поверхности ошибок:

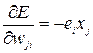. (3.7)

Градиент указывает направление, в котором скорость нарастания функции ошибки максимальна. Умножая градиент на скорость обучения, а также учитывая, что движение по поверхности ошибки осуществляется в сторону антиградиента (ведь ищем минимум, не так ли?), получаем:

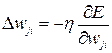 (3.8)

Вербально дельта-правило можно определить следующим образом:

Корректировка, применяемая к синаптическому весу нейрона, пропорциональна про­изведению сигнала ошибки на входной сигнал, его вызвавший:

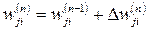 (3.9)

Пошаговая корректировка синаптических весов нейрона к продолжается до тех пор, пока сеть не достигнет устойчивого состояния, при котором значения весов практически стабилизируются. В этой точке процесс обучения останавливается.

Обучение на примерах характеризуется тремя основными свойствами: емкостью, сложностью образцов и вычислительной сложностью. Емкость соответствует количеству образцов, которые может запомнить сеть. Сложность образцов определяет способности нейронной сети к обучению. В частности, при обучении ИНС могут возникать состояния «перетренировки» («переобучение»), в которых сеть хорошо функционирует на примерах обучающей выборки, но не справляется с новыми примерами, утрачивая способность обучаться.

Алгоритм обратного распространения ошибки

Многослойный персептрон в состоянии решать произвольные задачи. Но долгое время его использование было затруднительно из-за отсутствия эффективного алгоритма обучения. При нескольких слоях настраиваемых весов становится непонятным, какие именно веса подстраивать в зависимости от ошибки сети на выходе. В 1986 г. Румельхарт, Хинтон и Вильяме предложили так называемый алгоритм обратного распространения ошибки (back-propagation).

Алгоритм обратного распространения определяет два потока в сети: прямой поток, от входного слоя к выходному, и обратный поток – от выходного слоя к входному. Прямой поток, также называемый функциональным потоком, продвигает входные сигналы через сеть, в результате чего в выходном слое получаются выходные значения сети. Обратный поток подобен прямому, но продвигает назад по сети значения ошибок, в результате чего определяются величины, в соответствии с которыми следует корректировать весовые коэффициенты в процессе обучения. В обратном потоке значения проходят по взвешенным связям в направлении, обратном направлению прямого потока. Наличие двойного потока в сети иллюстрирует рис. 3.2.

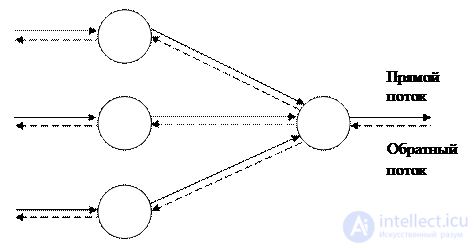
Рисунок 3.2 – Двойной поток в сети.

Сигнал ошибки выходного слоя вычисляется так же, как и в случае однослойного персептрона, так как для выходного слоя известны эталонные значения и энергия ошибки вычисляется непосредственно. Если нейрон расположен в скрытом слое сети, желаемый отклик для него неизвестен. Следовательно, сигнал ошибки скрытого нейрона должен рекурсивно вычисляться на основе сигналов ошибки всех нейронов, с которым он непосредственно связан.

Обозначим ошибку нейрона в некотором слое j следующим образом:

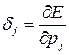; (3.10)

где p_j = Σw_jiz_i – взвешенная сумма входов нейрона;

z_i – входы нейрона и соответственно выходы предыдущего слоя нейронов.

Применяя правило дифференциорвания сложно функции, находим выражение для значения ошибки нейрона в выходном слое:

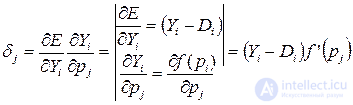 (3.11)

Для нейрона в скрытом слое выражение выводится с учетом, что нейрон посылает сигнал нейронам в следующем слое, для которых ошибка вычисляется по выражению (3.11):

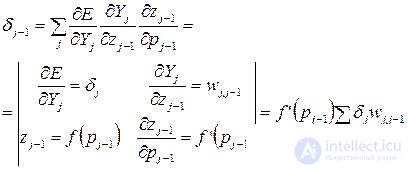 (3.12)

Таким образом, ошибка на каждом слое вычисляется рекурсивно через значения ошибки на предыдущих слоях: коррекция ошибки распространяется обратно по нейронной сети.

Усовершенствования алгоритма обратного распространения

Функция энергии ошибки E_P представляет собой довольно сложную овражистую поверхность с большим числом локальных минимумов (рис.3.3). Если при градиентном спуске попасть в такой минимум, то, очевидно, сеть не будет настроена на оптимальную производительность.

Рисунок 3.3 – Функция с овражным эффектом

Существует несколько путей решения проблем, связанных с локальными минимумами.

1. Простейший способ – это использование переменной скорости обучения η. В начале работы алгоритма ее величина представляет собой большое значение, близкое к 1, по мере сходимости η последовательно уменьшается. Это позволяет быстро подойти к минимуму, а затем точно попасть в него.

2. «Овражный» метод. Учитываются тенденции в поверхности добавлением момента инерции:

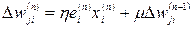 (3.13)

Где μ – положительное число, называемое постоянной момента.

Выражение (3.13) называют обобщенным дельта-правилом. Идея заключается в скачке через локальные минимумы в поверхности ошибки.

3. Метод сопряженных градиентов. Флетчер и Ривс предложили выбирать направление, сопряженное градиенту, более точно указывающее именно на минимум функции:

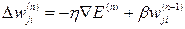 (3.14)

Где 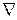– векторный дифференциальный оператор;

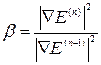
4. Наиболее точное решение – это решение, которое позволяют получить так называемые методы второго порядка. Общий принцип работы основан на использовании матрицы вторых производных – гессиана .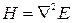

В общем, мой друг ты одолел чтение этой статьи об сети типа персептрон задача классификации образов обучение с учителем. Работы впереди у тебя будет много. Смело пиши комментарии, развивайся и счастье окажется в твоих руках. Надеюсь, что теперь ты понял что такое сети типа персептрон задача классификации образов обучение с учителем и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Интеллектуальные информационные системы