Покрытие множества и матрицы, Звездно-конечное покрытие в комбинаторной топологии кратко

Привет, Вы узнаете о том , что такое покрытие множества, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое покрытие множества, звездно-конечное покрытие, покрытие матрицы , настоятельно рекомендую прочитать все из категории Элементы комбинаторной и дифференциальной топологии.Дифференциальная геометрия и топология.

Покрытием множества A называется такое семейство непустых его подмножеств A1, . . . , Ak , что

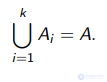
. Другими словами, если A1, . . . , Ak – покрытие множества A, то любой элемент a ∈ A лежит хотя бы в одном из множеств A1, . . . , Ak .

В отличие от разбиения в покрытии не требуется, чтобы множества A1, . . . , Ak не пересекались.

Покрытие в математике ( комбинаторной топологии)— семейство множеств, таких, что их объединение содержит заданное множество.

Обычно покрытия рассматривается в общей топологии, где наибольший интерес представляют открытые покрытия — семейства открытых множеств. В комбинаторной геометрии важную роль играют покрытия выпуклыми множествами.

звездно-конечное покрытие — это такое покрытие, что всякий его элемент пересекается лишь с конечным числом элементов этого покрытия. Часто под покрытием множества A всегда понимается звездно-конечное открытое (т. е. состоящее из открытых множеств) покрытие множества A.

Будем рассматривать матрицы из нулей единиц, не содержащие нулевых столбцов.

Покрытием матрицы M размера m × n называется такое такое подмножество ее строк i₁, . . . , i_k , что для каждого j, j = 1, . . . , n, найдется такой номер s = s(j), 1 ≤ s(j) ≤ k, что m_s(j),j = 1.

Другими словами, подмножество строк i₁, . . . , i_k матрицы M является ее покрытием, если в подматрице, образованной этими строками нет нулевых столбцов. покрытие матрицы также называется покрытием столбцов матрицы ее строками.

Определения

• Пусть дано множество . Семейство множеств называется покрытием , если

• Пусть дано топологическое пространство , где — произвольное множество, а — определенная на топология. Об этом говорит сайт https://intellect.icu . Тогда семейство открытых множеств называется открытым покрытием множества , если

Связанные определения

• Если — покрытие множества , то любое подмножество , также являющееся покрытием , называется подпокры́тием.
• Если каждый элемент одного покрытия является подмножеством какого-либо элемента второго покрытия, то говорят, что первое покрытие впи́сано во второе. Более точно, покрытие вписано в покрытие , если

такое, что

• Покрытие множества называется лока́льно коне́чным, если для каждой точки существует окрестность , пересекающаяся лишь с конечным числом элементов , то есть множество конечно.
• Покрытие множества называется фундамента́льным, если всякое множество, пересечение которого с каждым множеством открыто в , открыто и в .
• называется компактным, если любое его открытое покрытие содержит конечное подпокрытие;
• называется паракомпактным, если в любое его открытое покрытие можно вписать локально конечное открытое покрытие.

Покрывающий размер

Говорят, что топологическое пространство X имеет размерность покрытия n, если каждое открытое покрытие X имеет точечно-конечное открытое уточнение, такое, что никакая точка X не входит в более чем n + 1 множества в уточнении, и если n - минимальное значение для чего это правда. Если такого минимального n не существует, пространство называется бесконечной покрывающей размерностью.

Пример покрытия матрицы

Пример 1. Пусть

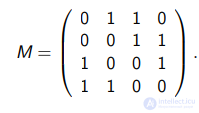
Тогда 1-я и 2-я строки не покрывают матрицу

а 1-я и 3-я строки – являются покрытием матрицы M:

Свойства

• Любое подпокрытие вписано в изначальное покрытие. Обратное, вообще говоря, неверно.

Вау!! 😲 Ты еще не читал? Это зря!

• Карта, Атлас ( математика )
• Нерв покрытия
• Размерность Лебега
• Покрытие графа
• Звездное уточнение
• Градиентное покрытие матрицы
• Кратчайшее покрытие матрицы
• тень набора
• тень множества наборов

Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области покрытие множества имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое покрытие множества, звездно-конечное покрытие, покрытие матрицы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Элементы комбинаторной и дифференциальной топологии.Дифференциальная геометрия и топология