Лекция
Привет, Вы узнаете о том , что такое атлас (топология), Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое атлас (топология), карта (топология) , настоятельно рекомендую прочитать все из категории Элементы комбинаторной и дифференциальной топологии.Дифференциальная геометрия и топология.
Атлас — понятие дифференциальной геометрии, позволяющие вводить на многообразии дополнительные структуры; например гладкую структуру или комплексную структуру.
Атлас состоит из отдельных карт, которые описывают отдельные области многообразия. Если под многообразием понимать поверхность Земли, то слова карта и атлас приобретают свои обычные значения.
Атласы - это инструмент, позволяющий придавать дифференцируемую структуру топологическим пространствам, являясь основой понятий дифференциальной геометрии многообразий .
Пусть 
— числовое поле (например 
или 
), 
— топологическое пространство.
, где
— открытое множество в
— гомеоморфизм из в открытое множество в 
криволинейные координаты, сопоставляя точке 
набор чисел 
и 
пересекаются (
), то между множествами 
и 
имеются взаимно обратные отображения (гомеоморфизмы), называемые функциями сличения или отображением склейки :
, 
, такое, что 
образует покрытие пространства . Об этом говорит сайт https://intellect.icu . Здесь 
— некоторое множество индексов. При этом атлас называется гладким (класса 
) или аналитическим, если функции замены координат 
для всех карт гладкие (класса ) или аналитические.Карта переходов дает возможность сравнить две диаграммы атласа. Чтобы сделать это сравнение, мы рассматриваем состав одной диаграммы с инверсией другой. Эта композиция не является четко определенной, если мы не ограничим обе карты пересечением их областей определения. (Например, если у нас есть карта Европы и карта России, то мы можем сравнить эти две карты на их пересечении, а именно европейскую часть России.)
Чтобы быть более точным, предположим, что 
и 
две карты для многообразия M такие, что
является непустым . Карта перехода 
карта определяется
Обратите внимание, что поскольку 
и 
оба являются гомеоморфизмами, отображение перехода 
также является гомеоморфизмом.
Часто на многообразии требуется больше структуры, чем просто топологическая структура. Например, если нужно получить однозначное понятие дифференцирования функций на многообразии, необходимо построить атлас, функции переходов которого дифференцируемы . Такое многообразие называется дифференцируемым . Учитывая дифференцируемое многообразие, можно однозначно определить понятие касательных векторов, а затем производных по направлениям .
Если каждая функция перехода является гладким отображением , то атлас называется гладким атласом , а само многообразие называется гладким . В качестве альтернативы можно потребовать, чтобы карты переходов имели только k непрерывных производных, и в этом случае атлас называется.
В общем случае, если каждая функция перехода принадлежит псевдогруппе 
гомеоморфизмов евклидова пространства, то атлас называется -атлас. Если карты переходов между картами атласа сохраняют локальную тривиализацию , то атлас определяет структуру пучка волокон.
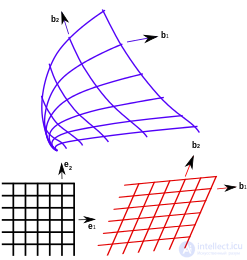
Криволинейные , аффинные и декартовы координаты в двумерном пространстве.
Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области атлас (топология) имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое атлас (топология), карта (топология) и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Элементы комбинаторной и дифференциальной топологии.Дифференциальная геометрия и топология
Из статьи мы узнали кратко, но содержательно про атлас (топология)
Комментарии
Оставить комментарий
Элементы комбинаторной и дифференциальной топологии.Дифференциальная геометрия и топология
Термины: Элементы комбинаторной и дифференциальной топологии.Дифференциальная геометрия и топология