Лекция
Привет, Вы узнаете о том , что такое магнитное поле в вакууме, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое магнитное поле в вакууме , настоятельно рекомендую прочитать все из категории Переменный электрический ток. Электромагнитное поле.
Еще в глубокой древности было известно, что некоторые минералы, например магнитный железняк (химический состав 31 % — Fe, 69 % — O), способны притягиваться друг к другу, а также притягивать к себе кусочки железа. Такие тела называются магнитами. Наибольшей силой притяжения обладают противоположные концы магнита, которые называются магнитными полюсами (рис. 6.1).
Рис. 6.1. Постоянные магниты различной формы
Ранее мы рассмотрели виток с током и связали с ним, характеризующий его свойства, вектор магнитного момента 
, где 
— нормаль к плоскости витка, направление которой задается правилом буравчика (рис. 6.2). Момент сил
Рис. 6.2. Виток с током во внешнем магнитном поле
стремится повернуть виток. Чтобы увеличить угол 
между магнитным моментом витка и направлением магнитной индукции поля, надо совершить работу
которая увеличивает потенциальную энергию витка dP = –dA. Отсюда
|
|
(6.1) |
Энергия достигает своего минимума, когда магнитный момент витка становится параллельным вектору магнитной индукции поля (
); антипараллельное положение (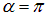
) соответствует неустойчивому положению равновесия. Все это означает, что виток с током ведет себя подобно магнитной стрелке (магнитному диполю). К тому же виток с током невозможно разделить на два независимых полюса — северный и южный. Мы пришли к гипотезе Ампера: все магнитные явления в конечном счете порождаются элементарными токами, текущими в структурных единицах вещества.
Иллюстрациями аналогичного поведения магнитной стрелки (магнита) и тока в проводе служат следующие опыты:
Рис. 6.3. Вращение магнитной стрелки
Рис. 6.4. Магнитные стрелки ориентируются по касательным к
силовым линиям магнитного поля постоянного магнита и соленоида
Рис. 6.5. Воздействие на провод с током
Магнитная стрелка — не только прибор, регистрирующий внешнее магнитное поле, она сама является маленьким магнитом, создающим свое собственное поле. Значит, и виток с током должен создавать свое собственное магнитное поле, подобное полю стрелки. Следовательно, любой электрический ток в проводнике создает вокруг него магнитное поле. В частности, такое поле должен создавать движущийся электрический заряд.
Сейчас мы попробуем угадать, какое магнитное поле порождается зарядом q, движущимся со скоростью v (рис. 6.6). Отправной точкой нам послужит аналогия между электрическими и магнитными явлениями. Вспомним то, что мы уже знаем. Чтобы получить силу, действующую на заряд в электростатическом поле, мы умножаем величину заряда на вектор напряженности поля
Рис. 6.6. Магнитное поле движущегося заряда
Чтобы получить силу Лоренца, действующую со стороны магнитного поля на движущийся заряд, мы тоже производим операцию умножения: векторно умножаем 
на магнитную индукцию
Применим тот же прием для угадывания магнитного поля движущегося заряда.
Электрическое поле покоящегося точечного заряда равно
Заменим q на вектор , электрическое поле — на магнитное, а операцию обычного умножения — на векторное умножение. Получаем
Мы не поставили здесь знака равенства, так как у нас не все в порядке с размерностью в левой и правой частях уравнения. Из выражения для силы Лоренца следует, что размерность магнитной индукции равна
Размерность же правой части уравнения равна
Чтобы размерности обеих частей совпали, правую часть надо разделить на квадрат какой-то скорости. Скорость частицы у нас уже использована, и остается единственная возможность — фундаментальная физическая постоянная, скорость света с
|
|
(6.2) |
Мы ввели здесь новую константу 
, связанную с 
соотношением
|
|
(6.3) |
Ее называют магнитной постоянной; численное значение ее оказывается равным
|
|
(6.4) |
Конечно, выражение (6.2) получено лишь по аналогии и не может рассматриваться, как строго выведенное. Однако посмотрим, к каким следствиям оно приводит.
Возьмем элемент проводника 
, по которому течет ток I (рис. 6.7). Направление вектора I 
, называемого элементом тока, совпадает с направлением тока в проводнике, то есть с направлением вектора 
дрейфовой скорости положительных зарядов.
Рис. 6.7. Магнитное поле, создаваемое элементом тока
Полный заряд носителей тока в этом элементе равен dq = enSdl, где е — заряд носителей, n — их концентрация, a S — поперечное сечение проводника. Подставим этот заряд в выражение (6.2) и получим (рис. 6.8)
Сила тока дается выражением
откуда, учитывая, что
получаем
|
|
(6.5) |
Рис. 6.8. Направление вектора индукции магнитного поля
Вектор 
проведен от элемента тока к точке наблюдения А. Соответственно, модуль вектора 
равен
|
|
(6.6) |
где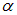 
— угол между направлением данного элемента тока 
1820 г. Био (рис. 6.9) и Саваром (рис. 6.10) и сформулированным Лапласом (рис. 6.11)
Рис. 6.9. Ж. Био (1774–1862) — французский физик, геодезист и астроном
Рис. 6.10. Ф. Савар (1791–1841) — французский физик
Рис. 6.11. П. Лаплас (1749–1827) — французский математик, физик и астроном
Закон Био — Савара — Лапласа определяет магнитную индукцию 
в любой точке магнитного поля, создаваемого постоянным электрическим током, текущим по проводнику любой формы (см. рис. 6.7). Для этого надо проинтегрировать соотношение (6.5) вдоль всего проводника. При этом магнитные индукции от различных элементов тока векторно складываются, то есть используется принцип суперпозиции для магнитных полей.
Вычислим поле, создаваемое током, текущим по тонкому прямолинейному проводу бесконечной длины.
Индукция магнитного поля в произвольной точке А (рис. 6.12), создаваемого элементом проводника dl, будет равна
Рис. 6.12. Магнитное поле прямолинейного проводника
Поля от различных элементов имеют одинаковое направление (по касательной к окружности радиусом R, лежащей в плоскости, ортогональной проводнику). Значит, мы можем складывать (интегрировать) абсолютные величины 
|
|
(6.7) |
Выразим r и sin 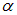через переменную интегрирования l
|
|
(6.8) |
Тогда (6.7) переписывается в виде
Таким образом,
|
|
(6.9) |
Картина силовых линий магнитного поля бесконечно длинного прямолинейного проводника с током представлена на рис. 6.13.
Рис. 6.13. Магнитные силовые линии поля прямолинейного проводника с током:
1 — вид сбоку; 2, 3 — сечение проводника плоскостью, перпендикулярной проводнику
Для обозначения направления тока в проводнике, перпендикулярном плоскости рисунка, будем использовать следующие обозначения (рис. 6.14):
Рис. 6.14. Обозначения направления тока в проводнике
Для обозначения направления тока в проводнике, перпендикулярном плоскости рисунка, будем использовать следующие обозначения (рис. 6.14):
Напомним выражение для напряженности электрического поля тонкой нити, заряженной с линейной плотностью заряда 
Сходство выражений очевидно: мы имеем ту же зависимость от расстояния до нити (тока), линейная плотность заряда заменилась на силу тока. Но направления полей различны. Для нити электрическое поле направлено по радиусам. Силовые линии магнитного поля бесконечного прямолинейного проводника с током образуют систему концентрических окружностей, охватывающих проводник. Направления силовых линий образуют с направлением тока правовинтовую систему.
На рис. 6.15 представлен опыт по исследованию распределения силовых линий магнитного поля вокруг прямолинейного проводника с током. Толстый медный проводник пропущен через отверстия в прозрачной пластинке, на которую насыпаны железные опилки. После включения постоянного тока силой 25 А и постукивания по пластинке опилки образуют цепочки, повторяющие форму силовых линий магнитного поля.
Вокруг прямого провода, перпендикулярного пластинке, наблюдаются кольцевые силовые линии, расположенные наиболее густо вблизи провода. При удалении от него поле убывает.
Рис. 6.15. Визуализация силовых линий магнитного поля вокруг прямолинейного проводника
На рис. 6.16 представлены опыты по исследованию распределения силовых линий магнитного поля вокруг проводов, пересекающих картонную пластинку. Железные опилки, насыпанные на пластинку, выстраиваются вдоль силовых линий магнитного поля.
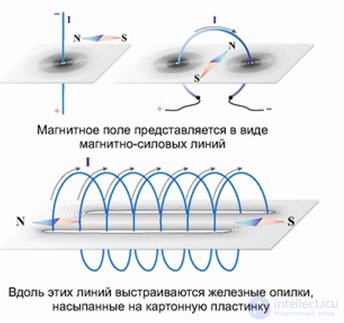
Рис. 6.16. Распределение силовых линий магнитного поля
вблизи пересечения с пластинкой одного, двух и нескольких проводов
Напряженность магнитного поля на оси кругового тока (рис. 6.17-1), создаваемого элементом проводника Idl, равна
поскольку в данном случае
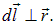
Рис. 6.17. Магнитное поле на оси кругового тока (слева) и электрическое поле на оси диполя (справа)
При интегрировании по витку вектор 
будет описывать конус, так что в результате «выживет» только компонента поля вдоль оси 0z. Поэтому достаточно просуммировать величину
|
|
(6.10) |
Интегрирование
выполняется с учетом того, что подынтегральная функция не зависит от переменной l, а
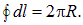
Соответственно, полная магнитная индукция на оси витка равна
|
|
(6.11) |
В частности, в центре витка (h = 0) поле равно
|
|
(6.12) |
На большом расстоянии от витка (h >> R) можно пренебречь единицей под радикалом в знаменателе. Об этом говорит сайт https://intellect.icu . В результате получаем
|
|
(6.13) |
Здесь мы использовали выражение для модуля магнитного момента витка Рm , равное произведению I на площадь витка 
Магнитное поле образует с круговым током правовинтовую систему, так что (6.13) можно записать в векторной форме
|
|
(6.14) |
Для сравнения рассчитаем поле электрического диполя (рис. 6.17-2). Электрические поля от положительного и отрицательного зарядов равны, соответственно,
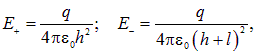
так что результирующее поле будет
|
|
(6.15) |
На больших расстояниях (h >> l) имеем отсюда
|
|
(6.16) |
Здесь мы использовали введенное в (3.5) понятие вектора электрического момента диполя 
. Поле Е параллельно вектору дипольного момента, так что (6.16) можно записать в векторной форме
|
|
(6.17) |
Аналогия с (6.14) очевидна.
Силовые линии магнитного поля кругового витка с током показаны на рис. 6.18. и 6.19
Рис. 6.18. Силовые линии магнитного поля кругового витка с током на небольших расстояниях от провода
Рис. 6.19. Распределение силовых линий магнитного поля кругового витка с током в плоскости его оси симметрии.
Магнитный момент витка направлен по этой оси
На рис. 6.20 представлен опыт по исследованию распределения силовых линий магнитного поля вокруг кругового витка с током. Толстый медный проводник пропущен через отверстия в прозрачной пластинке, на которую насыпаны железные опилки. После включения постоянного тока силой 25 А и постукивания по пластинке опилки образуют цепочки, повторяющие форму силовых линий магнитного поля.
Магнитные силовые линии для витка, ось которого лежит в плоскости пластинки, сгущаются внутри витка. Вблизи проводов они имеют кольцевую форму, а вдали от витка поле быстро спадает, так что опилки практически не ориентируются.
Рис. 6.20. Визуализация силовых линий магнитного поля вокруг кругового витка с током
Пример 1. Электрон в атоме водорода движется вокруг протона по окружности радиусом аB = 53 пм (эту величину называют радиусом Бора по имени одного из создателей квантовой механики, который первым вычислил радиус орбиты теоретически) (рис. 6.21). Найти силу эквивалентного кругового тока и магнитную индукцию В поля в центре окружности.
Рис. 6.21. Электрон в атоме водорода
Решение. Заряды электрона и протона одинаковы по величине (е) и противоположны по знаку. На электрон действует сила кулоновского притяжения протона, создающая центростремительное ускорение
откуда находим угловую скорость движения электрона по круговой орбите
Период обращения электрона вокруг ядра равен
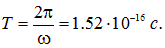
Если представить себе воображаемую площадку, ортогональную траектории электрона, то за время Т через нее проходит заряд е. Поэтому сила эквивалентного тока равна
Скорость движения электрона равна v = 
аB = 2,18·106 м/с. Движущийся заряд создает в центре орбиты магнитное поле
Этот же результат можно получить с помощью выражения (6.12) для поля в центре витка с током, силу которого мы нашли выше
Пример 2. Бесконечно длинный тонкий проводник с током 50 А имеет кольцеобразную петлю радиусом 10 см (рис. 6.22). Найти магнитную индукцию в центре петли.
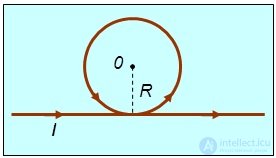
Рис. 6.22. Магнитное поле длинного проводника с круговой петлей
Решение. Магнитное поле в центре петли создается бесконечно длинным прямолинейным проводом и кольцевым витком. Поле от прямолинейного провода направлено ортогонально плоскости рисунка «на нас», его величина равна (см. (6.9))
Поле, создаваемое кольцеобразной частью проводника, имеет то же направление и равно (см. 6.12)
Суммарное поле в центре витка будет равно
|
Соленоидом называется цилиндрическая катушка, состоящая из большого числа витков провода, образующих винтовую линию (рис. 6.23-1). |
Рис. 6.23. Магнитные силовые линии поля: 1 — соленоида; 2 — полосового магнита
Магнитное поле соленоида напоминает поле полосового магнита (рис. 6.23-2).
Если витки намотаны вплотную, то соленоид — это система круговых токов, имеющих одну ось.
Если считать соленоид достаточно длинным, то магнитное поле внутри соленоида однородно и направлено параллельно оси. Вне соленоида вдали от краев магнитное поле также должно иметь направление параллельное оси и на большом расстоянии от соленоида должно быть очень слабым. Поле убывает по закону
Подсчитаем поле внутри соленоида. Возьмем элемент соленоида длиной dh, находящийся на расстоянии h от точки наблюдения. Если катушка имеет n витков на единицу длины, то в выделенном элементе содержится ndh витков. Согласно формуле (6.11), этот элемент создает магнитное поле
|
|
(6.18) |
Интегрируя по всей длине соленоида, получаем
|
|
(6.19) |
Таким образом, поле в бесконечно длинном соленоиде дается выражением
|
|
(6.20) |
На практике соленоиды бесконечно длинными не бывают. Для иллюстрации рассмотрим некоторые примеры.
Пример 1. Найти магнитное поле в середине соленоида конечной длины l (рис. 6.24). Сравнить с полем бесконечно длинного соленоида. При каких условиях разница составляет менее 0,5 %?
Рис. 6.24. Магнитное поле катушки конечной длины
В центре соленоида магнитное поле практически однородно и значительно превышает по модулю поле вне катушки
Решение. Магнитное поле в средней точке оси соленоида конечной длины l дается тем же интегралом (6.19), но с другими пределами интегрирования
|
|
(6.21) |
Если длина соленоида много больше его диаметра (l >> 2R), мы возвращаемся к формуле для поля в бесконечно длинном соленоиде (6.20). Относительная разница этих двух значений равна
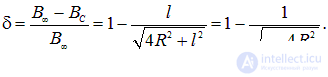
По условию эта разница мала: 
, то есть мало отношение диаметра соленоида к его длине: 2R/l << 1. Поэтому можно воспользоваться формулой разложения квадратного корня
Отсюда
или
Подставляя численное значение d, находим, что разница будет менее половины процента при выполнении соотношения
Иными словами, соленоид может рассматриваться как бесконечно длинный, если его длина в двадцать или более раз превышает радиус.
Пример 2. Найти магнитное поле Ве в крайней торцевой точке оси соленоида конечной длины l. Сравнить с результатом предыдущего примера.
Решение. Магнитное поле в торцевой точке оси соленоида конечной длины l дается тем же интегралом (6.19), но теперь пределы интегрирования будут выглядеть иначе
|
|
(6.22) |
Отношение полей в средней и крайней точках оси соленоида равно
Это отношение всегда меньше единицы (то есть поле на торце меньше поля в середине соленоида). При l >> R имеем
Этот результат легко понять. Представим себе бесконечный соленоид, который мысленно рассекаем пополам в точке наблюдения. Можно считать, что поле в этой точке создается двумя одинаковыми «полубесконечными» соленоидами, расположенными по разные стороны от нее. Ясно, что при удалении одного из них точка наблюдения становится торцом оставшегося «полубесконечного» соленоида, а магнитная индукция в ней уменьшиться именно в два раза.
Это — так называемый краевой эффект. Пример демонстрирует, что недостаточно выполнения соотношения l >> R, чтобы пользоваться формулами для бесконечно длинного соленоида; надо еще, чтобы точка наблюдения находилась далеко от его концов.
На рис. 6.25 представлен опыт по исследованию распределения силовых линий магнитного поля вокруг соленоида. Поле соленоида, ось которого лежит в плоскости пластинки, сосредоточено в основном внутри соленоида. Силовые линии внутри имеют вид параллельных прямых вдоль оси катушки, а поле снаружи практически отсутствует.
Рис. 6.25. Визуализация силовых линий магнитного поля
Применим закон Ампера для вычисления силы взаимодействия двух длинных прямолинейных проводников с токами I1 и I2, находящихся на расстоянии d друг от друга (рис. 6.26).
Рис. 6.26. Силовое взаимодействие прямолинейных токов:
1 — параллельные токи; 2 — антипараллельные токи
Видео 6.2. Взаимодействие двух параллельных проводников с током.
Проводник с током I1 создает кольцевое магнитное поле, величина которого в месте нахождения второго проводника равна
|
|
(6.23) |
Это поле направлено «от нас» ортогонально плоскости рисунка. Элемент второго проводника 
испытывает со стороны этого поля действие силы Ампера
|
|
(6.24) |
Подставляя (6.23) в (6.24), получим
|
|
(6.25) |
При параллельных токах сила F21 направлена к первому проводнику (притяжение), при антипараллельных — в обратную сторону (отталкивание).
Аналогично на элемент 
проводника 1 действует магнитное поле, создаваемое проводником с током I2 в точке пространства с элементом с силой F12. Рассуждая таким же образом, находим, что F12 = –F21, то есть в этом случае выполняется третий закон Ньютона.
Итак, сила взаимодействия двух прямолинейных бесконечно длинных параллельных проводников, рассчитанная на элемент длины проводника, пропорциональна произведению сил токов I1 и I2 протекающих в этих проводниках, и обратно пропорциональна расстоянию между ними. В электростатике по аналогичному закону взаимодействуют две длинные заряженные нити.
На рис. 6.27 представлен опыт, демонстрирующий притяжение параллельных токов и отталкивание антипараллельных. Для этого используются две алюминиевые ленты, подвешенные вертикально рядом друг с другом в слабо натянутом состоянии. При пропускании через них параллельных постоянных токов силой около 10 А ленты притягиваются. а при изменении направления одного из токов на противоположное — отталкиваются.
Рис. 6.27. Силовое взаимодействие длинных прямолинейных проводников с током
На основании формулы (6.25) устанавливается единица силы тока — ампер, являющаяся одной из основных единиц в СИ.
|
Ампер — это сила неизменяюшегося тока, который, протекая по двум длинным параллельным проводникам, расположенным в вакууме на расстоянии 1 м, вызывает между ними силу взаимодействия 2×10–7 Н на каждый метр длины провода. |
Пример. По двум тонким проводам, изогнутым в виде одинаковых колец радиусом R = 10 см, текут одинаковые токи I = 10 А в каждом. Плоскости колец параллельны, а центры лежат на ортогональной к ним прямой. Расстояние между центрами равно d = 1 мм. Найти силы взаимодействия колец.
Решение. В этой задаче не должно смущать, что мы знаем лишь закон взаимодействия длинных прямолинейных проводников. Поскольку расстояние между кольцами много меньше их радиуса, взаимодействующие элементы колец «не замечают» их кривизны. Поэтому сила взаимодействия дается выражением (6.25), куда вместо надо подставить длину окружности колец 
Получаем тогда
|
Потоком вектора магнитной индукции В (магнитным потоком) через малую поверхность площадью dS называется скалярная физическая величина, равная
|
Здесь 
, 
— единичный вектор нормали к площадке площадью dS, Вn — проекция вектора В на направление нормали, 
— угол между векторами В и n (рис. 6.28).
Рис. 6.28. Поток вектора магнитной индукции через площадку
Магнитный поток ФB через произвольную замкнутую поверхность S равен
|
|
(6.27) |
Отсутствие в природе магнитных зарядов приводит к тому, что линии вектора В не имеют ни начала, ни конца. Поэтому поток вектора В через замкнутую поверхность должен быть равен нулю. Таким образом, для любого магнитного поля и произвольной замкнутой поверхности S выполняется условие
|
|
(6.28) |
Формула (6.28) выражает теорему Остроградского — Гаусса для вектора 
:
|
Поток вектора магнитной индукции через произвольную замкнутую поверхность тождественно равен нулю. |
Подчеркнем еще раз: эта теорема является математическим выражением того факта, что в природе отсутствуют магнитные заряды, на которых начинались бы и заканчивались линии магнитной индукции, как это имело место в случае напряженности электрического поля Е точечных зарядов.
Это свойство существенным образом отличает магнитное поле от электрического. Линии магнитной индукции замкнуты, поэтому число линий, входящих в некоторый объем пространства, равно числу линий, выходящих из этого объема. Если входящие потоки брать с одним знаком, а выходящие — с другим, то суммарный поток вектора магнитной индукции через замкнутую поверхность будет равен нулю.
|
В системе СИ единицей измерения магнитного потока является вебер (Вб) (рис. 6.29):
|
Рис. 6.29. В. Вебер (1804–1891) — немецкий физик
Отличие магнитного поля от электростатического проявляется также в значении величины, которую мы называем циркуляцией — интеграла от векторного поля по замкнутому пути. В электростатике равен нулю интеграл
взятый по произвольному замкнутому контуру. Это связано с потенциальностью электростатического поля, то есть с тем фактом, что работа по перемещению заряда в электростатическом поле не зависит от пути, но лишь от положения начальной и конечной точек.
Посмотрим, как обстоит дело с аналогичной величиной для магнитного поля. Возьмем замкнутый контур, охватывающий прямой ток, и вычислим для него циркуляцию вектора В, то есть
Как было получено выше, магнитная индукция, создаваемая прямолинейным проводником с током на расстоянии R от проводника, равна
Рассмотрим случай, когда контур, охватывающий прямой ток, лежит в плоскости, перпендикулярной току, и представляет собой окружность радиусом R с центром на проводнике. В этом случае циркуляция вектора В по этой окружности равна
|
|
(6.29) |
откуда
|
|
(6.30) |
Можно показать, что результат для циркуляции вектора магнитной индукции не меняется при непрерывной деформации контура, если при этой деформации контур не пересекает линий тока. Тогда в силу принципа суперпозиции циркуляция вектора магнитной индукции по пути, охватывающем несколько токов, пропорциональна их алгебраической сумме (рис. 6.30)
|
|
(6.31) |
Рис. 6.30. Замкнутый контур (L) с заданным направлением обхода.
Изображены токи I1, I2 и I3, создающие магнитное поле.
Вклад в циркуляцию магнитного поля вдоль контура (L) дают только токи I2 и I3
Если выбранный контур не охватывает токов, то циркуляция 
по нему равна нулю.
При вычислении алгебраической суммы токов следует учитывать знак тока: положительным будем считать ток, направление которого связано с направлением обхода по контуру правилом правого винта. Например, вклад тока I2 в циркуляцию — отрицательный, а вклад тока I3 — положительный (рис. 6.18). Воспользовавшись соотношением
между силой тока I через любую замкнутую поверхность S и плотностью тока 
, для циркуляции вектора В можно записать
|
|
(6.32) |
где S — любая замкнутая поверхность, опирающаяся на данный контур L.
Итак,
|
Циркуляция магнитной индукции отлична от нуля, если контур, по которому она берется, охватывает ток. |
Такие поля называются вихревыми. Поэтому для магнитного поля нельзя ввести потенциал, как это было сделано для электрического поля точечных зарядов. Наиболее наглядно разницу потенциального и вихревого полей можно представить по картине силовых линий. Силовые линии электростатического поля похожи на ежей: они начинаются и кончаются на зарядах (либо уходят в бесконечность). Силовые линии магнитного поля никогда не напоминают «ежей»: они всегда замкнуты и охватывают текущие токи.
Для иллюстрации применения теоремы о циркуляции найдем другим методом уже известное нам магнитное поле бесконечного соленоида. Возьмем прямоугольный контур 1-2-3-4 (рис. 6.31) и вычислим циркуляцию вектора В по этому контуру
|
|
(6.33) |
Рис. 6.31. Применение теоремы о циркуляции В к определению магнитного поля соленоида
Второй и четвертый интегралы равны нулю в силу перпендикулярности векторов 
и 
. Третий интеграл можно положить равным нулю, ввиду малости магнитного поля вне соленоида. Поэтому
|
|
(6.34) |
Рассмотренный контур охватывает суммарный ток nlI, где n — число витков соленоида, приходящееся на единицу длины, I — сила тока в соленоиде. Следовательно,
или
|
|
(6.35) |
Мы воспроизвели результат (6.20) без интегрирования магнитных полей от отдельных витков.
Полученный результат (6.35) можно использовать для нахождения магнитного поля тонкого тороидального соленоида (рис.6.32).
Рис. 6.32. Тороидальная катушка: линии магнитной индукции замыкаются внутри катушки и представляют собой концентрические окружности. Они направлены так, что глядя вдоль них, мы увидели бы ток в витках, циркулирующим по часовой стрелке. Одна из линий индукции некоторого радиуса r1 ≤ r < r2 изображена на рисунке
Связь между электричеством и магнетизмом не исчерпывается похожестью ряда соотношений. В сущности, оба эти поля суть разные проявления единого электромагнитного поля. В курсе механики мы говорили о принципе относительности, о том, что все законы природы должны быть инвариантными при переходе из одной инерциальной системы отсчета в другую. Однако электрическое и магнитное поля сами по себе, по отдельности, явно не удовлетворяют этому принципу. Действительно, находясь в инерциальной системе отсчета К, возьмем заряд q, движущийся прямолинейно и равномерно со скоростью v. Он создает кулоновское электрическое поле и, помимо этого, магнитное поле, вектор индукции которого дается выражением (6.2). Свяжем с зарядом систему отсчета К ', которая также будет инерциальной. В этой системе отсчета заряд покоится, и создаваемое им поле будет чисто электростатическим. Выходит, электрическое и магнитное поля не имеют абсолютного характера. При переходе к другой системе отсчета они должны преобразовываться друг через друга (рис. 6.33).
Рис. 6.33. Заряд покоится в движущейся системе отсчета
Вспомним преобразования Лоренца для пространственных координат и времени
|
|
(6.36) |
Не забудем, что аналогичные преобразования связывают импульс и энергию частицы в разных системах отсчета
|
|
(6.37) |
Станем ли мы теперь удивляться, что электрическое и магнитное поля в разных системах отсчета также связаны преобразованиями Лоренца
|
|
(6.38) |
Напомним, что величины со штрихом относятся к системе отсчета К ', которая движется относительно системы К вдоль оси х со скоростью V.
Из преобразований Лоренца следует, что электрическое поле движущегося заряда вытягивается в направлении перпендикулярном скорости (рис. 6.34).
Рис. 6.34. Электрическое поле движущегося заряда
Заметим, что формулы преобразований Лоренца для электромагнитного поля отличаются от преобразований для пространства-времени или энергии-импульса тем, что не преобразуются компоненты полей вдоль линии движения системы отсчета К ' (то есть вдоль оси 0х). Чтобы проиллюстрировать это, рассмотрим лабораторную систему отсчета К, в которой имеется электрическое поле Е, но нет магнитного (В = 0). В каком случае наблюдатель движущейся системы отсчета К ' тоже будет наблюдать лишь чисто электрическое поле Е ' без примеси магнитного (В ' = 0)? Ответ следует из формул (6.38) при подстановке туда нулевых значений для В, В ': из второго уравнения сразу вытекает Е 'y = Е 'z = 0, а из первого — Еу = Ez = 0. Иными словами, такое возможно, когда электрическое поле (не обязательно однородное) направлено вдоль движения системы отсчета К '.
Уравнения электромагнетизма изначально были инвариантны относительно этих преобразований, так что теория относительности вполне безболезненно совместилась с электромагнитной теорией, в то время как классическая механика подверглась существенной ревизии. Вместо обоснования справедливости преобразований (6.38), что выходит за рамки нашего курса, мы познакомимся еще с одним их следствием.
Поскольку мы пока занимаемся в основном нерелятивистской физикой, упростим преобразования Лоренца для случая, когда скорость системы отсчета К ' много меньше скорости света: V << с. В этом случае, как уже отмечалось, квадратные корни
и преобразования (6.38) принимают вид
|
|
(6.39) |
Эти уравнения можно записать в векторной форме
|
|
(6.40) |
Вернемся к нашей заряженной частице, покоящейся в системе К '. В этой системе магнитное поле отсутствует (В ' = 0), а электрическое поле дается законом Кулона
Поскольку предполагается V << с, мы используем преобразования Галилея для пространственных координат и временных интервалов, так что радиус-вектор, проведенный от частицы в точку наблюдения, одинаков в обеих системах отсчета: r = r '. Подставляя указанные выражения для В ', Е ' в преобразования (6.40), получаем
|
|
(6.41) |
Здесь мы использовали соотношение (6.3)
Первое уравнение (6.41) — обычное кулоновское поле заряда q, второе — магнитное поле движущегося заряда (6.2). Таким образом, даже классический магнетизм — это проявление релятивистских эффектов. Электрическое и магнитное поля оказываются неразрывно связанными друг с другом в единое электромагнитное поле, конкретное проявление которого зависит от системы отсчета.
Пример. Самолет летит горизонтально со скоростью 250 м/с в магнитном поле Земли с магнитной индукцией 50 мкТл, направленной вертикально вниз. Какое электромагнитное поле будут наблюдать пассажиры самолета?
Решение. Направим ось 0х системы лабораторной отсчета К, связанной с Землей, вдоль маршрута самолета, так что его скорость запишется в виде
Ось 0z направим вертикально вверх, так что магнитная индукция описывается вектором
Нам надо найти электрическое и магнитное поля в движущейся системе отсчета К ', связанной с самолетом. Поскольку скорость самолета много меньше скорости света, мы можем применить формулы (6.40). Для удобства, однако, мы используем обратные формулы, получаемые заменой штрихованных величин на нештрихованные и изменением знака скорости: V = –v:
|
|
(6.42) |
Так как в лабораторной системе электрического поля нет (Е = 0), то из второго уравнения сразу следует, что В ' = В: магнитное поле для авиапассажиров останется тем же, что и для проводивших их в полет родственников. Однако, в самолете появится еще и электрическое поле. Его напряженность, как вытекает из первого уравнения, равна
|
|
(6.43) |
Мы использовали здесь тот факт, что векторное произведение двух ортов дает третий орт
60 м на их концах создается разность потенциалов 
— величина небольшая, но доступная измерениям.
Исследование, описанное в статье про магнитное поле в вакууме, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое магнитное поле в вакууме и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Переменный электрический ток. Электромагнитное поле
Комментарии
Оставить комментарий
Переменный электрический ток. Электромагнитное поле
Термины: Переменный электрический ток. Электромагнитное поле