Привет, сегодня поговорим про эволюционные технологии, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое эволюционные технологии, эволюционные алгоритмы , настоятельно рекомендую прочитать все из категории Интеллектуальные информационные системы.

Основные понятия и определения

Эволюция – это многоэтапный процесс возникновения органических форм с более высокой степенью организации, который характеризуется изменчивостью самих эволюционных механизмов. Эволюционное моделирование можно определить как воспроизведение процесса естественной эволюции с помощью специальных компьютерных программ. Необходимые и достаточные условия, определяющие главные факторы эволюции, были сформулированы в XX в. К факторам, определяющим неизбежность эволюции, относятся:

• 1) наследственная изменчивость как предпосылка эволюции, ее материал;
• 2) борьба за существование как контролирующий и направляющий фактор;
• 3) естественный отбор как преобразующий фактор.

На рис. 10.1 приведена конкретизация факторов эволюции, учитывающая многообразие форм их проявления, взаимосвязей и взаимовлияния. Главные факторы выделены пунктиром.

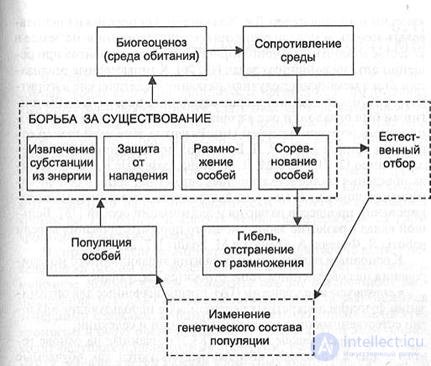
Рисунок 10.1 – Взаимосвязь факторов эволюции.

Современная теория эволюции базируется на теории общей и популяционной генетики. Элементарным объектом эволюции является популяция — сообщество свободно скрещивающихся особей. В популяциях происходят микроэволюционные процессы, приводящие к изменению их генофонда. Преобразования генетического состава популяции происходят под действием элементарных эволюционных факторов. Случайные структурные или функциональные изменения в генах, хромосомах и других воспроизводимых единицах называет мутациями, если они приводят к наследственному изменению какого-либо фенотипического признака особи. Хромосомы это специфические структуры клеточного ядра, которые играют важнейшую роль в процессах деления клеток. Хромосомы состоят из генов. Геном называется реально существующая, независимая, комбинирующаяся и расщепляющаяся при скрещиваниях единица наследственности. Преобразования генофонда популяции происходят под управлением естественного отбора.

История эволюционных вычислений началась с разработки ряда независимых моделей, среди которых были генетические алгоритмы и классификационные системы, созданные американским исследователем Дж. Холландом. Он предложил использовать методы и модели развития органического мира на Земле в качестве механизма комбинаторного перебора вариантов при решении оптимизационных задач. Компьютерные реализации этого механизма получили название «генетические алгоритмы».

К основным направлениям развития эволюционного моделирования на современном этапе относятся следующие:

• – генетические алгоритмы (ГА), предназначенные для оптимизации функций дискретных переменных и использующие аналогии естественных процессов рекомбинации и селекции;
• – классифицирующие системы (КС), созданные на основе генетических алгоритмов, которые используются как обучаемые системы управления;
• – генетическое программирование (ГП), основанное на использовании эволюционных методов для оптимизации создаваемых компьютерных программ;
• – эволюционное программирование (ЭП), ориентированное на оптимизацию непрерывных функций без использования рекомбинаций;
• – эволюционные стратегии (ЭвС), ориентированные на оптимизацию непрерывных функций с использованием рекомбинаций.

Эволюционные методы целесообразно использовать в тех случаях, когда прикладную задачу сложно сформулировать в виде, позволяющем найти аналитическое решение, или тогда, когда требуется быстро найти приближенный результат, например, при управлении системами в реальном времени.

Генетические алгоритмы

Генетический алгоритм – это поисковый алгоритм, основанный на природных механизмах селекции и генетики. Эти алгоритмы обеспечивают выживание сильнейших решений из множества сгенерированных, формируя и изменяя процесс поиска на основе моделирования эволюции исходной популяции решений. Генетические алгоритмы сконструированы таким образом, что при генерации каждой новой популяции используются фрагменты исходных решений, к которым добавляются новые элементы, обеспечивающие улучшение решений относительно сформулированного критерия отбора.

При разработке генетических алгоритмов преследуются две главные цели:

1) абстрактное и формальное объяснение процессов адаптации в естественных системах;

2) проектирование искусственных программных систем, воспроизводящих механизмы функционирования естественных систем.

Основные отличия ГА от других алгоритмов оптимизации:

1) используются не параметры, а закодированные множества параметров;

2) поиск осуществляется не из единственной точки, а из популяции точек;

3) в процессе поиска используются значения целевой функции, а не ее приращения;

4) применяются вероятностные, а не детерминированные правила поиска и генерации решений;

5) выполняется одновременный анализ различных областей пространства решений, в связи с чем возможно нахождение новых областей с лучшими значениями целевой функции за счет объединения квазиоптимальных решений из разных популяций.

В основе генетических алгоритмов лежат генетика и хромосомная теория эволюции организмов. Классическая генетика обосновала наследственность и изменчивость благодаря созданию фундаментальной теории гена, основные положения которой формулируются следующим образом:

1. все признаки организма определяются наборами генов;

2. гены – это элементарные единицы наследственной информации, которые находятся в хромосомах;

3. гены могут изменяться – мутировать;

4. мутации отдельных генов приводят к изменению отдельных элементарных признаков организма, или фенов.

Термины, взятые из генетики, трактуются а ГА следующим образом:

Генетика	Генетические алгоритмы
Хромосома	Решение, стринг, строка, последовательность, родитель, потомок
Популяция	Набор решений (хромосом)
Локус	Местоположение гена в хромосоме
Ген	Элемент, характеристика, особенная черта, свойство, детектор
Поколение	Цикл работы генетического алгоритма, в процессе которого сгенерировано множество решений
Аллель	Значение элемента, характеристики
Эпистасис	Множество параметров, альтернативные решения

Каждое решение из множества возможных можно представить набором информации, который может быть изменен путем введения в него элементов другого решения. Другими словами, возможные решения соответствуют хромосомам, состоящим из генов, причем в ходе оптимизации происходит обмен генами между хромосомами – рекомбинация. Об этом говорит сайт https://intellect.icu . Рекомбинация используется для накопления в конечном решении лучших функциональных признаков, какие имелись в наборе исходных решений.

Хромосомы – это нитевидные структуры, находящиеся в клеточном ядре, которые являются носителями наследственности. Каждая хромосома уникальна морфологически и генетически и не может быть заменена другой либо восстановлена при утере (при потере хромосомы клетка, как правило, погибает). Каждый биологический вид имеет определенное, постоянное количество хромосом. Каждая клетка содержит удвоенный набор морфологически и генетически сходных хромосом. Например, в клетках человека содержится 23 пары хромосом, в клетках комара – 3.

Ген определяется как структурная единица наследственной информации, далее неделимая в функциональном отношении. Комплекс генов, содержащихся в наборе хромосом одного организма, образует геном.

Существует несколько типов рекомбинации участков хромосом. В генетических алгоритмах наибольшее распространение получила операция кроссинговера, заключающаяся в разрыве гомологичных хроматид с последующим соединением их в новом сочетании. Он приводит к появлению нового сочетания сцепленных генов. Схема кроссинговера, демонстрирующая образование двух новых хромосом после обмена генетическим материалом, приведена на рис. 10.2. Основная цель кроссинговера заключается в создании из имеющегося генетического материала желаемой комбинации признаков в одном решении.

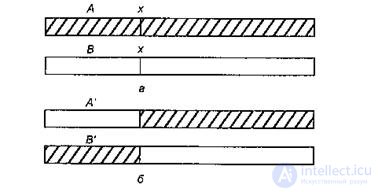
Рисунок 10.2 – Схема кроссинговера:
а) родительские хромосомы до кроссинговера,
б) хромосомы-потомки после кроссинговера.

Кроссинговер может происходить в нескольких точках. Пример двойного кроссинговера между хромосомами приведен на рис. 10.3.

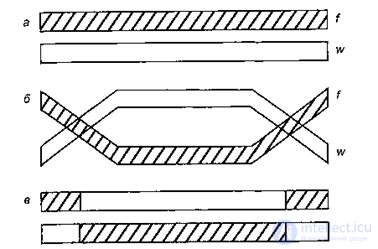
Рисунок 10.3 – Схема двойного кроссинговера:
а) до кроссинговера, б) во время кроссинговера,
в) после кроссинговера.

Помимо кроссинговера для решения различных прикладных задач полезными являются такие генетические операции, как мутация, инверсия, транслокация, селекция, генная инженерия.

Под мутацией понимается генетическое изменение, приводящее к качественно новому проявлению основных свойств генетического материала. Применение операции мутации в генетических алгоритмах направлено на получение решений, которые не могут быть улучшены качественно посредством кроссинговера.

Инверсия, транслокация, транспозиция, делеция и дупликация относятся к разновидностям хромосомной мутации. При инверсии участок хромосомы поворачивается на 180°. Транслокацией называют перенос части одной хромосомы в другую. При перемещении небольших участков генетического материала в пределах одной хромосомы используют термин транспозиция. Делеция — это выпадение отдельных участков хромосом, дупликация – повторение участка генетического материала. Кроме перечисленных, существуют другие разновидности хромосомных мутаций.

Простой генетический алгоритм

Согласно Холланду генетические схемы поиска оптимальных решений включают следующие этапы процесса эволюции:

1. Конструируется начальная популяция. Вводится начальная точка отсчета поколений t = 0. Вычисляются приспособленность хромосом популяции (целевая функция) и средняя приспособленность всей популяции.

2. Устанавливается значение t = t+1. Выбираются два родителя (хромосомы) для кроссинговера. Выбор осуществляется случайным образом пропорционально жизнеспособности хромосом, которая характеризуется значениями целевой функции.

3. Формируется генотип потомка. Для этого с заданной вероятностью над генотипами выбранных хромосом производится операция кроссинговера. Случайным образом выбирается один из потомков A(t), к которому с заданными вероятностями последовательно применяются операторы инверсии и мутации. Полученная хромосома сохраняется как A’(t).

4. Обновление текущей популяции путем замены случайно выбранной хромосомы на A’(t).

5. Определение приспособленности A’(t) и пересчет средней приспособленности популяции.

6. Если t=t*, где t* – заданное число шагов, то переход к этапу 7, в противном случае – переход к этапу 2.

7. Конец работы.

Основная идея эволюции, заложенная в различные конструкции генетических алгоритмов, проявляется в способности «лучших» хромосом оказывать большее влияние на состав новой популяции за счет длительного выживания и более многочисленного потомства.

Простой генетический алгоритм включает операцию случайной генерации начальной популяции хромосом и ряд операторов, обеспечивающих генерацию новых популяций на основе начальной. Этими операторами являются репродукция, кроссинговер и мутация.

Репродукцией называется процесс копирования хромосом с учетом значений целевой функции, т.е. хромосомы с «лучшими» Значениями целевой функции имеют большую вероятность попадания в следующую популяцию. Этот процесс является аналогией митозного деления клеток. Выбор клеток (хромосом) для репродукции проводится в соответствии принципом «выживания сильнейшего». Простейшим способом представления операции репродукции в алгоритмической форме является колесо рулетки, в котором каждая хромосома имеет поле, пропорциональное значению целевой функции.

В алгоритмических реализациях механизма воспроизводства хромосом следует придерживаться следующих правил.

1. Выбор начальной популяции можно выполнять произвольным образом, например подбрасыванием монеты.

2. Репродукция осуществляется на основе моделирования движения колеса рулетки.

3. Оператор кроссинговера реализуется как взаимный обмен короткими фрагментами двоичных строк гомологичных хромосом.

4. Вероятность оператора кроссинговера принимается равной Р(CO)<1.

5. Вероятность оператора мутации принимается равной Р(МO)>0.001.

Рассмотрим пример применения простого генетического алгоритма для максимизации функции f(x)=x² на целочисленном интервале [0, 31] .

Значения аргумента функции изменяющегося в интервале от 0 до 31, можно представить пятиразрядными двоичными числами. Первоначальная популяция, состоящая из четырех пятиразрядных чисел, получена с помощью процедуры генерации случайных чисел.

Анализ начальной популяции на первом шаге простого генетического алгоритма:

Номер хромосомы	Значение х (десятичный код)	Двоичный код хромосомы	Значение целевой функции	Вероятность выбора	Ожидаемое количество копий хромосомы в следующем поколении	Реальное количество копий хромосомы в следующем поколении
				0.14 0.49 0.06 0.31	0.56 1.96 0.24 1.24
Сумма		1.00	4.00
Среднее значение		0.25	1.00
Максимальное значение		0.49	1.97

Вероятность выбора i-й хромосомы вычисляется по формуле

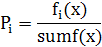
где fi(x) — значение целевой функции i-й хромосомы в популяции; sumf(x) – суммарное значение целевой функции всех хромосом в популяции.

Ожидаемое число копий i-й хромосомы после оператора репродукции равно

N = P_in;

где n — Число анализируемых хромосом.

Репродукция начального множества заключается в четырехкратном вращении колеса рулетки (4 - мощность популяции), в результате чего состав исходной популяции может измениться.

Рисунок 10.4 – Колесо рулетки.

Следует заметить, что колесо рулетки не гарантирует выбора лучших хромосом, т.е. иногда результатом выбора могут оказаться хромосомы с низкими значениями целевой функции.

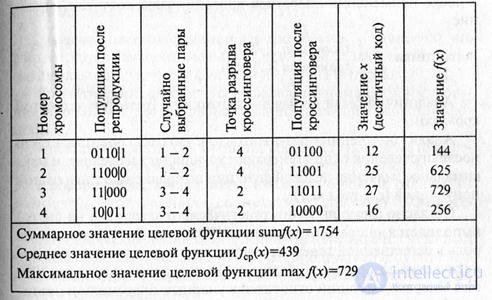
После репродукции выполняется оператор кроссинговера, который может повторяться несколько раз. При этом каждый раз будет осуществляться выбор двух кандидатур из множества хромосом. Затем каждая пара хромосом пересекается. Место пересечения К выбирается случайным образом на интервале (1, L-1), где L – длина хромосомы, определяемая количеством значащих цифр в ее двоичном коде. В нашем случае L = 5. Две новые хромосомы создаются путем взаимного обмена всех значений после точки пересечения, т.е. между позициями (К+1) и L. При выборе двух первых хромосом из популяции (см. табл) и значения К = 4 до применения оператора кроссинговера имеем описание:

хромосома1: 0110|1

хромосома2: 1100|0

После применения оператора кроссинговера получаем описание:

хромосома1: 0110|0

хромосома2: 1100|1

Аналогично были получены потомки от третьей и четвертой хромосом.

Анализ полученных результатов показывает, что после проведения одной генерации улучшились и среднее, и максимальное значение целевой функции по сравнению с начальной популяцией.

Согласно схеме простого генетического алгоритма на шаге 3 выполняется оператор мутации, который играет существенную роль в естественной генетике и эволюции, но менее значим в генетических алгоритмах. Обычно выбирают одну мутацию на 1000 бит. Оператор мутации относится к унарным операциям и реализуется в два этапа.

Этап 1. В хромосоме А = {а₁, а₂, a₃…a_L-2, a_L-1, a_L} случайным образом определяют две позиции, например, 2 и L-1.

Этап 2. Гены, соответствующие выбранным позициям, меняют местами и формируют новую хромосому А = {а₁, a_L-1, a₃,…, a_L-2, a₂, a_L}

Если длина обрабатываемых последовательностей невелика, то в процессе мутации можно осуществить полный перебор возможных перестановок генов и найти комбинацию с максимальным значением целевой функции. Выберем третью хромосому 11011 со значением целевой функции f(х)=729 и применим операцию мутации к позициям 3 и 4:

хромосома 3: 11011 -> хромосома 3': 11101.

У новой хромосомы 3' значение целевой функции равно (29)²=841. Сделаем еще одну перестановку 4 и 5 генов в хромосоме 3':

хромосома 3': 11101 –> хромосома 3": 11110.

Значение целевой функции для хромосомы 3" равно 900, что соответствует квазиоптимальному решению задачи нахождения максимального значения функции f(х)=x² на интервале [0,31].

Разновидности генетических алгоритмов

Генетический алгоритм Девиса включает следующие шаги:

1. Инициализация популяции хромосом.

2. Оценка каждой хромосомы в популяции.

3. Создание новых хромосом посредством изменения и скрещивания текущих хромосом (применение операторов мутации и кроссинговера).

4. Устранение хромосом из популяции для замены их новыми.

5. Оценка новых хромосом и включение их в популяцию.

6. Проверка условия исчерпания ресурса времени, отведенно¬го на поиск оптимального решения (если время исчерпано, то работа алгоритма завершается и производится возврат к наилучшей хромосоме, в противном случае – переход к шагу 3).

Холланд предложил для генетического алгоритма оператор инверсии, который реализуется по схеме:

1. Стринг (хромосома) В = {b_x, b₂,…, b_L} выбирается случайным образом из текущей популяции.

2. Из множества Y{0,1,2, L + 1} случайным образом выбираются два числа у₁ и у₂ и определяются значения x₁=min{y₁,y₂} и x₂=max{y₁,y₂}.

3. Из хромосомы В формируется новая хромосома путем ин- -Jверсии (обратного порядка) сегмента, лежащего справа от позиции x₁ и слева от позиции х₂ вхромосоме В. После применения оператора инверсиистрока В примет вид В'={b₁,…, b_x1,b_x2-1,b_x2-2,…,b_x1+1,b_x2,…,b_L}.

Например, для строки В={1, 2, 3, 4, 5, 6} при выборе у₁=6 и y₂=2 соответственно x₁ =2, x₂= 6 результатом инверсии будет B^’={1, 2, 5, 4, 3, 6}.

Операции кроссинговера и мутации, используемые в простом IX, изменяют структуру хромосом, в том числе разрушают удачные фрагменты найденных решений, что уменьшает вероятность нахождения глобального оптимума. Для устранения этого недостатка в генетических алгоритмах используют схемы (схематы или шаблоны), представляющие собой фрагменты решений или хромосом, которые желательно сохранить в процессе эволюции. При использовании схем в генетическом алгоритме вводится новый алфавит {0,1,*}, где * интерпретируется как «имеет значение 1 или 0». Например: схема (*0000) соответствует двум стрингам {10000 и 00000};

• - схема (*111*) соответствует четырем строкам {01110, 11110, 01111,11111};
• - схема (0*1**) может соответствовать восьми пятизначным стрингам.

В общем случае хромосома длиной L максимально может иметь 3^L схем (шаблонов), но только 2^L различных альтернативных стрингов. Это следует из факта, что схеме (**) в общем случае могут соответствовать 3²=9 стрингов, а именно {**, *1, *0, 1*, 0*, 00, 01, 10, 11}, и только 2²=4 альтернативные строки {00,01,10,11}, т. е. одной и той же строке может соответствовать несколько схем.

Если в результате работы генетического алгоритма удалось найти схемы типа (11***) и (**111), то применив оператор кроссинговера, можно получить хромосому (11111), обладающую наилучшим значением целевой функции.

Схемы небольшой длины называются строительными блоками. Размер строительных блоков заметно влияет на качество и скорость нахождения результата. Вид строительного блока выбирается с учетом специфики решаемой задачи, а их разрыв в генетических алгоритмах допускается только в исключительных случаях, определяемых пользователем. Например, в схеме (****1) строительным блоком является элемент 1, а в схеме (10***) – составной элемент 10.

При использовании большого числа строительных блоков генетические алгоритмы, основанные на случайной генерации популяций и хромосом, переходят в разряд беспорядочных.

Стационарные генетические алгоритмы отличаются от поколенческих тем, что у первых размер популяции является заданным постоянным параметром, который определяется пользователем, а у вторых размер популяции в последующих генерациях может увеличиваться или уменьшаться.

Процедура удаления лишних хромосом в стационарных и поколенческих генетических алгоритмах основана на эвристических правилах, примерами которых являются следующие:

• - случайное равновероятное удаление хромосом;
• - удаление хромосом, имеющих худшие значения целевой функции;
• - удаление хромосом на основе обратного значения целевой функции;
• - удаление хромосом на основе турнирной стратегии.

Следует иметь в виду, что использование в генетических алгоритмах тех или иных эвристик удаления хромосом может повлечь за собой негативные последствия. Например, удаление худших хромосом приводит к преждевременной утрате разнообразия и, как следствие, к попаданию целевой функции в локальный оптимум, а при наличии большого числа хромосом с плохими значениями целевой функции утрачивается направленность поиска, и он превращается в «слепой» поиск.

В общем, мой друг ты одолел чтение этой статьи об эволюционные технологии. Работы впереди у тебя будет много. Смело пиши комментарии, развивайся и счастье окажется в твоих руках. Надеюсь, что теперь ты понял что такое эволюционные технологии, эволюционные алгоритмы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Интеллектуальные информационные системы