Хуа-Няо - понятие и значение

Рассмотрим что означает понятие и значение слова хуа-няо (информация предоставлена intellect.icu).

Тоже самое что слово - живопись,

1. А) Искусство изображать предметы и явления реального мира с помощью красок. б) Произведения такого искусства.
2. Манера изображения как особый жанр этого искусства.

1. Изобразительное искусство - создание художественных образов с помощью красок. Уроки живописи. Школа живописи. 2. собцр. Произведения этого искусства. Стенная женский род Станковая женский род

1. Живописи, ( книжное ). Искусство изображать предметы красками. Брать уроки живописи.
2. Произведения этого искусства. Живопись на стенах потрескалась. Голландская, итальянская живопись.
3. Манера изображения, как особый жанр этого искусства. Батальная живопись.

-и, женский род

1.

Вид изобразительного искусства, воспроизводящий предметы и явления реального мира с помощью красок.

Заниматься живописью. Уроки живописи.

Характер, манера изображения, свойственная этому виду искусства.

Одна {картина} привлекла мое внимание. --- Поразила меня в ней не живопись, а то, что картина была прострелена двумя пулями, всаженными одна на другую. Пушкин, Выстрел.

Его {Верещагина} живопись (собственно письмо) такого высокого качества, которое стоит в уровень с тем, что мы знаем в Европе. Его колорит, в общем, поразителен. Крамской, Письмо П. М. Третьякову, 12 марта 1874.

2. собирательное

Произведения этого вида искусства: картины, фрески, росписи и т. падеж

Выставка живописи.

Коридор этот, как и во многих старинных церквах, был почти темный, но с живописью на стенах из ветхого завета. Писемский, Тысяча душ.

Синонимы

рисование, картина, искусство, роспись, пастель, бундзинга, граффито, суйбокуга, направление, иконопись, воспроизведение, краска, изография, гохуа, левкас, суйбоку-га, механографика, питтура кольта, нихонга, алла прима, жэнь-у, ямато-э, кара-э, стенопись, витро, ёга, сфумато, энкаустика, асекко, живопись

Рифмы

Данное слово имеет следующие слова-рифмы:

Рифмы для этого же слова "хуа-няо", но если ударение на последний слог :
хуацяо.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "хуа-няо" :
ганемоняо, вувоьеняо, синониняо, бовавеняо, рыпйроняо, ферясяняо, кавануняо, шокосеняо.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Хуа-няо" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-Х500, для metaphone-"хуанa" и для double-metaphone KN.

См. также

... переговоры были четырехсторонними : США , Северный Вьетнам ., проамериканская Республика Вьетнам исозданное Ханоем наоснове НФОЮВ Временное .революционное правительство Республики Южный Вьетнам (ВРП РЮВ ... ... поэт сромантическим псевдонимом Суан Тхюи («Вешние .воды »;) Генри Киссинджер ипредставитель Ханоя Ле Дык Тхо (слева ) обмениваются .рукопожатием послесовещания впригороде Сен-Ном-ла-Бретеш , 12 ... (Всемирная история)

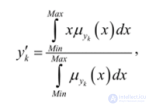... алгоритма Сугсно-Такаги (Takagi Т , Sugeno М ) является представление правил базы знаний в виде (ЕСЛИ *, /& - 0. ха есть -)ТО yt = с>(| + , +. +с j„x„. где Xj - /-я (i = 1 , 2 , n) входная лингвистическая переменная ., aij ... (Вычислительный интеллект)

... , необходимым условием существования аддитивной функции полезности является условие соответственных . замещений где Хв , Ха Хп - ЛКЗ в точках В, С и. О соответственно Можно доказать , что это условие является достаточным Процедура построения ... (Теория принятия решений)

... В соответствии с официальной формулировкой , под техни -. ческим уровнем (ТУ ) продукции понимается относительная ха -. рактеристика качества продукции , основанная на сопоставлении (соотношении ) значений показателей свойств , отражающих ... (Квалиметрия надежность и качество)

... Пример Традиционный (по закону обратного отношения между содержанием и объемом ). x(A(x)B (x)) (х). студент-отличник - студент - Дизъюнктивный хА (х) x (A (x)B (x)). студент - студент или школьник -. Введение существования хА (х,a)xyA (x,y). студент , знающий астрономию ... ... (х,a)xyA (x,y). студент , знающий астрономию - студент , знающий какую-то науку -. Удаление всеобщности (х,y)хА (х,a). студент , знающий любую науку - студент , знающий астрономию -. От способов обобщения ... (Логика)

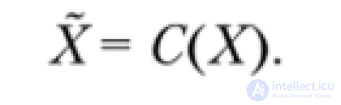... Обозначим через X множество наиболее предпочтительных вариантов для ЛПР , тогда . Хявляется подмножеством множества X: Ха X Функцией выбора С называется правило , ставящее в соответствие множеству X. его подмножество альтернатив X: С(Х) = X Таким ... (Теория принятия решений)

---

---