Хроматический - понятие и значение

Рассмотрим что означает понятие и значение слова хроматический (информация предоставлена intellect.icu).

1. Соотносящийся по значение с существительное : хроматизм (1*), связанный с ним (в музыке).
2. Свойственный хроматизму (1*), характерный для него.
3. Основанный на хроматизме (1*). 2. прилагательное Цветной, окрашенный.

1. Хроматическая, хроматическое. 1. прилагательное , по значение связанное с преломлением лучей, с хроматизмом ( физика ). Хроматическое разложение лучей. Хроматическая аберрация. 2. Состоящий из последовательного ряда полутонов, основанный на хроматизме ( (музыка) ). Хроматическая гамма.
2. Обозначающий повышение или понижение на полтона ( (музыка) ). Хроматические знаки. 3. Снабженный особым приспособлением для получения полутонов ( (музыка) ). Хроматические духовые инструменты.

ХРОМАТИЧЕСКИЙ

( греческое , т. т. разноцветный). 1) в греческой древней музыке: последовательность тонов из четырех интервалов (тетрахорд). В современной музыке: проследование и вообще всякое движение звуков в полутонах. 2) цветной.

ХРОМАТИЧЕСКИЙ

1) цветной; 2) относящийся к хроматической гамме.

ХРОМАТИЧЕСКИЙ

Имеющий движение полутонами.

ХРОМАТИЧЕСКИЙ

цветной; в музыке: составленный из полуто новое

1. Физ.

Основанный на явлениях хроматизма (в 1 значение ).

Хроматическое разложение лучей. Хроматическая аберрация (неточность изображения, получающаяся вследствие разложения света, проходящего через оптическую систему).

2. Муз.

Основанный на хроматизме (во 2 значение ), получившийся в результате хроматизма.

Хроматический звукоряд. Хроматический полутон. Хроматические интервалы.

В музыке есть хроматическая и есть искусственная обработка диссонан совершенный вид Юрьев, Записки.

3. Муз.

Снабженный особым приспособлением для получения полуто новое

Хроматическая гармонь.

Часть речи

Имя прилагательное (полное)

Словоформы

хроматического, хроматическому, хроматическим, хроматическом, хроматическая, хроматической, хроматическую, хроматическою, хроматическое, хроматические, хроматических, хроматическими

Синонимы

цветной, хроматичный

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "хроматический":
абазинский, аббатский, абверовский, абдеристический, абиссинский, аболиционистский, абонентский, абсолютистский, абстракционистский, абхазский, венгерский, высокий, героический, горнозаводский, горький, жидкий, лёгкий, психический, щегольский

Рифмы для этого же слова "хроматический", но если ударение на последний слог :
абецедарий.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "хроматический" :
ьывалекий, чосезикий, гетикукий, пакатыкий, диьамакий, гекенокий, нодынакий, вынадокий.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Хроматический" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-Х653, для metaphone-"хрaматичиский" и для double-metaphone KRMT.

См. также

... , простого граф , если не является ни полным графом ., ни графов-циклом Графы с большим хроматическим числом Графы с большими кликами имеют большое хроматическое число , но обратное . утверждение ... ... задача эквивалентна задаче о раскраске вершин графа с использованием . наименьшего числа цветов Хроматическое число графа как раз и соответствует осмотру , требующему наименьших . временных затрат Распределение ... (Алгоритмы и теория алгоритмов)

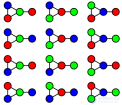... , ни вершины и ребра , которые их соединяют ,.не имеют одинакового цвета Полное хроматическое число графа - это наименьшее число цветов , необходимое для. любой полной раскраски Свойства ... ... ., иногда называемое деревом Зыкова Время выполнения зависит от метода выбора вершин и. Хроматический полином удовлетворяет рекуррентному соотношению :. , где и смежные вершины , граф с удалением ребра . представляет ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

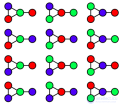... цветов называется раскраской Наименьшее число цветов , необходимое для раскраски графа , называется его хроматическим . числом и часто записывается как. Иногда используется , с тех пор как обозначает Эйлерову характеристику ... ... графа G так, чтобы концы любого ребра имели .разные цвета Обозначается χ(G). Определение Хроматическое число графа - минимальное число , такое что множество вершин графа . можно разбить ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

... цвета Все цвета делятся на две большие группы : цвета ахроматические и. цвета хроматические К ахроматическим относятся белый , черный и серый К хроматическим относятся все остальные цвета ... ... преимущественно волны определенной длины , а остальные поглощает , то предмет будет . окрашен в определенный хроматический цвет Ахроматические цвета отличаются друг от друга только светлотой Светлота зависит ... (Общая психология)

... вопреки трудности поиска такого множества для более общих семейств . графов Реберное хроматическое число графа G равно вершинному хроматическому числу его. реберного графа L(G). Реберный граф ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

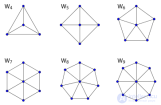... Вершин n Ребер 2 (n − Диаметр 2 при n>4 1 при n=4 Обхват 3 Хроматическое число 3 при нечетном n, 4 при четном n Свойства гамильтонов двойственный планарный Обозначение ... ... ( в OEIS ). 7 циклов в колесе W. Для нечетных значений n Wn является совершенным графом с хроматическим . числом 3 - вершины цикла можно выкрасить в два цвета , а.центральная вершина ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

---

---