1. Разбивка, деление геометрической поверхности на треугольники и вычисление углов и протяжений тригонометрическим способом.
2. Геодезический метод нахождения опорных точек на земной поверхности, служащих для топографических съемок и различных геодезических измерений на местности.
1. Триангуляции, (от латинское triangulus - треугольник). 1. Вычисление углов и протяжений методами тригонометрии ( математика ). 2. Определение взаимного расположения точек на поверхности при помощи построения сети треугольников ( геодезия ). 3. Вычисление длины дуги меридиана путем вычисления длины сторон последовательного ряда треугольников ( география ).
ТРИАНГУЛЯЦИЯ
(позд.-лат., от лат. triangalus - треугольник.). Тригонометрическое действие, при посредстве которого снимают план с известной местности, разделивши ее на треугольники, которые вычисляются при помощи тригонометрических формул.
ТРИАНГУЛЯЦИЯ
позд.-лат., от латинское triangulus, треугольник. Съемка местности посредством треугольников.
ТРИАНГУЛЯЦИЯ
прием, употребляемый при съемки планов с больших площадей, состоящий в том, что всю измеряемую поверхность разбивают на треугольники, у которых затем определяют углы; с помощью этих величин и известной длины к. кто-нибудь одной линии - так назыв. базиса - вычисляют все остальная стороны и площадь.
ТРИАНГУЛЯЦИЯ
топографическая съемка местности, состоящая в разбивке земной поверхности на треугольники. Делается это в виду того, что точное измерение длинных линий представляет большие затруднения, измерение же углов может быть произведено, при помощи теодолита, с большою точностью. Поэтому при съемке большого пространства ограничиваются измерением только одной линии - так называемый базиса - и затем, измеряя углы треугольников, на которые разбита местность, вычисляют все их стороны при помощи формул тригонометрии ( смотри ).
-и, женский род
1. Мат.
Разбивка поверхности на треугольники.
2. Геод.
Метод определения положения опорных точек на земной поверхности для топографической съемки местности.
{От лат. triangulum — треугольник}

 ... l ³ Любой граф .можно превратить в хордальный , добавив в него некоторое множество ребер Триангуляцией графа G = (V, E) называется хордальный граф H = (V., E¢), E Í E¢, который содержит G в качестве остовного .подграфа Триангуляция ... ... среди них выделить те., которые образуют клики в G;. - извлечь кликовые минимальные сепараторы из минимальной триангуляции H графа G. Рассмотрим вначале первый способ Известно , что множество S Í V является минимальным сепаратором графа ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)
... l ³ Любой граф .можно превратить в хордальный , добавив в него некоторое множество ребер Триангуляцией графа G = (V, E) называется хордальный граф H = (V., E¢), E Í E¢, который содержит G в качестве остовного .подграфа Триангуляция ... ... среди них выделить те., которые образуют клики в G;. - извлечь кликовые минимальные сепараторы из минимальной триангуляции H графа G. Рассмотрим вначале первый способ Известно , что множество S Í V является минимальным сепаратором графа ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)
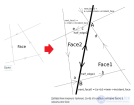 ... карт . К примеру , географическая карта в геоинформационной системе . Особым случаем ППЛГ являются триангуляция : триангуляция многоугольника , триангуляция множества точек . Многоточечная триангуляция является максимальной ППЛГ в том смысле ... ... в том смысле , что невозможно . прибавить к ним прямолинейные ребра , так чтобы граф остался планарным Триангуляции имеют многочисленные применения в разных областях ППЛГ может рассматриваться как особый вид ... (Алгоритмы и теория алгоритмов)
... карт . К примеру , географическая карта в геоинформационной системе . Особым случаем ППЛГ являются триангуляция : триангуляция многоугольника , триангуляция множества точек . Многоточечная триангуляция является максимальной ППЛГ в том смысле ... ... в том смысле , что невозможно . прибавить к ним прямолинейные ребра , так чтобы граф остался планарным Триангуляции имеют многочисленные применения в разных областях ППЛГ может рассматриваться как особый вид ... (Алгоритмы и теория алгоритмов)
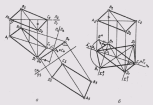 ... ,дающие истинную величину .основания и сечения пирамиды На рис 149 способом триангуляции построена развертка конической поверхности , которая заменена поверхностью . вписанной в нее двенадцатиугольной ... ... заменена поверхностью , вписанной правильной двенадцатиугольной пирамидой , а. для построения развертки применен способ триангуляции ... (11. Метрические задачи)
... ,дающие истинную величину .основания и сечения пирамиды На рис 149 способом триангуляции построена развертка конической поверхности , которая заменена поверхностью . вписанной в нее двенадцатиугольной ... ... заменена поверхностью , вписанной правильной двенадцатиугольной пирамидой , а. для построения развертки применен способ триангуляции ... (11. Метрические задачи)
 ... поверхностью вписанной правильной . двенадцатигранной призмы , и развертка цилиндрической поверхности построена способом триангуляции Положение точки М на развертке цилиндрической поверхности определяется обычным способом ... (11. Метрические задачи)
... поверхностью вписанной правильной . двенадцатигранной призмы , и развертка цилиндрической поверхности построена способом триангуляции Положение точки М на развертке цилиндрической поверхности определяется обычным способом ... (11. Метрические задачи)
 ... Основным алгоритмом оценки расстояния между точками поверхности деталей для оптических . систем является метод триангуляции , основу которого составляет алгоритм распознавания схожих .точек на двух сканах и расчет ... ... благодаря искажениям . проекции решетки , которые создает геометрия объектов За счет триангуляции полученных точек образуется полигональная поверхность - ее представление . возможно во всех распространенных ... (электромеханические устройства электронных аппаратов)
... Основным алгоритмом оценки расстояния между точками поверхности деталей для оптических . систем является метод триангуляции , основу которого составляет алгоритм распознавания схожих .точек на двух сканах и расчет ... ... благодаря искажениям . проекции решетки , которые создает геометрия объектов За счет триангуляции полученных точек образуется полигональная поверхность - ее представление . возможно во всех распространенных ... (электромеханические устройства электронных аппаратов)
 ... содержит ни вершин , ни ребер (на рис . 3 он не изображен ) Такую триангуляцию треугольника ABC можно построить следующим образом Сначала для каждого перекрестка и каждой ... (Теории узлов, зацеплений, кос и их инвариантов)
... содержит ни вершин , ни ребер (на рис . 3 он не изображен ) Такую триангуляцию треугольника ABC можно построить следующим образом Сначала для каждого перекрестка и каждой ... (Теории узлов, зацеплений, кос и их инвариантов)
Комментарии
Оставить комментарий