1. Процесс действия по значению глагол: наложить (1а1-3).
1. Наложения, средний род ( книжное ). Действие по глагол наложить в 1, 2, 3, 4, 5 и 9 значение - налагать.
-я, средний род
Действие по глагол наложить (во всех значение , кроме 5).
Наложение повязки. Наложение грима. Наложение печатей. Наложение взыскания.
... последних двух тождеств для пересечения отношений не имеют места . Типы отношений Сюръекция , инъекция и биекция - Отображение f:x>y называется СЮРЪЕКЦИЕЙ , если Ay ∈Y ∃ x.∈X:y=f(x). Тогда y - образ , x - прообраз y - Отображение ... ... , если f одновременно сюръективна и инъективна . Рисунок 9 иллюстрирует понятия отношения , функции , инъекции , сюръекции и биекции . Пример Рассмотрим три функции , заданные на множестве действительных чисел и принимающих ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)
... отображение отрезка наквадрат Доказательство Таккак2 N × 2 Nгомеоморфно 2 N, токвадрат f ×fотображения fявляетсясюръекцией множества 2 N (гомеоморфного канторову множеству C) наквадрат I2 Обозначим сюръекцию CнаI2 ... (Общая топология)
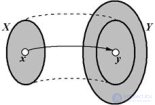... Рис 10 – Взаимно-однозначное отображение Х в Y (инъекция ). Отображение , которое является од новременно инъекцией и сюръекцией , называется Взаимно-однозначным . отображением Х на Y или биекцией (наложением ). Рис 11 – Взаимно-однозначное отображение Х на Y (биекция ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)
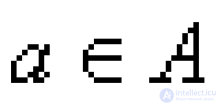... тех элементов из., образы которых принадлежат B, т е φ-1(B) = {: j(a) Î В}. Напомним , что отображение φ множества в множество называется . сюръекцией , если φ(M = M. Если для любых двух различных элементов и из. их образы = φ(x и = φ(x.также различны , то φ называется инъекцией ... ... различных элементов и из. их образы = φ(x и = φ(x.также различны , то φ называется инъекцией Отображение φ: , которое одновременно является сюръекцией и инъекцией ., называется биекцией или взаимно однозначным соответствием между и M. Имеют место следующие основные ... (Функциональный анализ)
... , согласно которому конечные множества конечны по Дедекинду : пусть A.и B - конечные множества Если есть сюръекция из A в B, которая не является. инъективной , то никакая сюръекция из A в B не является.инъективной Фактически , никакая функция ... ... : в общем случае он неверен для конечных множеств В техническом плане это говорит , что если и B конечные . множества такие , что любая Сюръекция от A до B не .инъективно , то существует элемент Ь из В таких , что существует взаимно . однозначное соответствие между прообраза ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)
... , 89 счетная полуаддитивность внешней меры , 56 счетно-аддитивная функция множеств , 52 сюръекция , 6 тело системы , 21 Теорема Арцела , 35 теорема Банаха о замкнутом ... (Функциональный анализ)
Комментарии