1. Сопряжённый прилагательное Неразрывно связанный с чем -либо , такой, которому непременно сопутствует что -либо другое.
1.
Прич. страдательное (причастие) прошедшее время от сопрячь.
2. в значение прилагательное Тех.
Взаимно связанный, находящийся во взаимодействии.
Сопряженные детали. Сопряженные поверхности. Сопряженные рессоры (две рессоры, концы которых связаны балансиром).

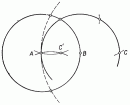 ... Сявляетсяодновременно точкой ихкасания идолжна лежать .налинии центров этих дуг Радиус сопряжения должен быть перпендикулярен кпрямой AB вточке .касания аПоэтому изцентра Оописываем ... ... кривой Следовательно , радиус сопряжения должен быть перпендикулярным кпрямой вточке .касания Сопряжение циркульных кривых возможно тогда , когда точка сопряжения будет являться .одновременно ... (Начертательная геометрия и инженерная графика)
... Сявляетсяодновременно точкой ихкасания идолжна лежать .налинии центров этих дуг Радиус сопряжения должен быть перпендикулярен кпрямой AB вточке .касания аПоэтому изцентра Оописываем ... ... кривой Следовательно , радиус сопряжения должен быть перпендикулярным кпрямой вточке .касания Сопряжение циркульных кривых возможно тогда , когда точка сопряжения будет являться .одновременно ... (Начертательная геометрия и инженерная графика)
 ... R - R1 , аиз.центра О2 - радиусом , равным R + R2 ак строить внутренние ивнешние сопряжения заданного радиуса дляокружностей .Припостроении сопряжения двух окружностей дугой третьей окружности ... ... окружностей дугой третьей окружности заданного радиуса .возможны три варианта : внешнее сопряжение , внутренне сопряжение исочетание внешнего .ивнутреннего сопряжений Передтем, какстроить сопряжения впрограмме AutoCAD ... (Начертательная геометрия и инженерная графика)
... R - R1 , аиз.центра О2 - радиусом , равным R + R2 ак строить внутренние ивнешние сопряжения заданного радиуса дляокружностей .Припостроении сопряжения двух окружностей дугой третьей окружности ... ... окружностей дугой третьей окружности заданного радиуса .возможны три варианта : внешнее сопряжение , внутренне сопряжение исочетание внешнего .ивнутреннего сопряжений Передтем, какстроить сопряжения впрограмме AutoCAD ... (Начертательная геометрия и инженерная графика)
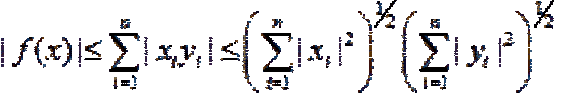 ... Пусть Е - нормированное пространство Совокупность всех ограниченных функционалов обозначается через Е* и называется сопряженным . пространством к Е Поскольку линейный функционал f : Е ® R можно рассматривать как линейный . оператор , действующий из Е в R, то сопряженное ... ... х. = {}, где ÎR, i = 1 , 2 , …, и имеет норму ||.x|| = |xi | Покажем , что каждый функционал f Îс* имеет вид Отсюда видно , что сопряженное пространство с* изометрично пространству абсолютно . суммируемых последовательностей y = {yi } с нормой ||y|| =. Пусть векторы ... (Функциональный анализ)
... Пусть Е - нормированное пространство Совокупность всех ограниченных функционалов обозначается через Е* и называется сопряженным . пространством к Е Поскольку линейный функционал f : Е ® R можно рассматривать как линейный . оператор , действующий из Е в R, то сопряженное ... ... х. = {}, где ÎR, i = 1 , 2 , …, и имеет норму ||.x|| = |xi | Покажем , что каждый функционал f Îс* имеет вид Отсюда видно , что сопряженное пространство с* изометрично пространству абсолютно . суммируемых последовательностей y = {yi } с нормой ||y|| =. Пусть векторы ... (Функциональный анализ)
 ... 35 , а) ивнутреннее (рис 35 , б) Втомивдругом случаеприпостроении сопрягающей дуги .радиуса Rцентр сопряжения Олежит напересечении геометрических мест .точек , равно удаленных отпрямой идуги радиуса ... ... .точек , равно удаленных отпрямой идуги радиуса Rнавеличину .R1 Припостроении внешнего сопряжения параллельно заданной прямой нарасстоянии R.1 всторону окружности проводят вспомогательную прямую ... (Начертательная геометрия и инженерная графика)
... 35 , а) ивнутреннее (рис 35 , б) Втомивдругом случаеприпостроении сопрягающей дуги .радиуса Rцентр сопряжения Олежит напересечении геометрических мест .точек , равно удаленных отпрямой идуги радиуса ... ... .точек , равно удаленных отпрямой идуги радиуса Rнавеличину .R1 Припостроении внешнего сопряжения параллельно заданной прямой нарасстоянии R.1 всторону окружности проводят вспомогательную прямую ... (Начертательная геометрия и инженерная графика)
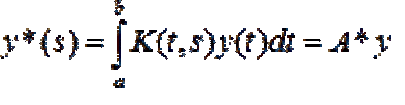 ... , y) = (x, A*y) = ( x, *y),. то отсюда по следствию 4 из теоремы Хана-Банаха следует , что. *y= A*y для всех y, а это означает ,.что A*=* Теорема 1 Сопряженный оператор A* - линейный и Доказательство Докажем аддитивность оператора A*. Действительно , если y, z ÎY*, то из рассуждений выше вытекает ... ... оператора А* проведем оценки Отсюда следует , что оператор A* - ограниченный и У оператора A*, в свою очередь , есть сопряженный - A**, определяемый . равенством , аналогичным (A*y, x) = (y, A**x). Но , так как из A**x определяется однозначно для каждого . , то из сопоставления равенств и следует ... (Функциональный анализ)
... , y) = (x, A*y) = ( x, *y),. то отсюда по следствию 4 из теоремы Хана-Банаха следует , что. *y= A*y для всех y, а это означает ,.что A*=* Теорема 1 Сопряженный оператор A* - линейный и Доказательство Докажем аддитивность оператора A*. Действительно , если y, z ÎY*, то из рассуждений выше вытекает ... ... оператора А* проведем оценки Отсюда следует , что оператор A* - ограниченный и У оператора A*, в свою очередь , есть сопряженный - A**, определяемый . равенством , аналогичным (A*y, x) = (y, A**x). Но , так как из A**x определяется однозначно для каждого . , то из сопоставления равенств и следует ... (Функциональный анализ)
 ... Припостроении сопряжения дуг окружностей прямой линией можно рассмотреть две .задачи : сопрягаемая прямая ... ... вспомогательной окружности , проведенной радиусом R. - RI Ееточку касания Коиспользуют дляпостроения точки сопряжения А.надуге радиуса RДляполучения второй точки сопряжения А1 надуге радиуса .R1 ... (Начертательная геометрия и инженерная графика)
... Припостроении сопряжения дуг окружностей прямой линией можно рассмотреть две .задачи : сопрягаемая прямая ... ... вспомогательной окружности , проведенной радиусом R. - RI Ееточку касания Коиспользуют дляпостроения точки сопряжения А.надуге радиуса RДляполучения второй точки сопряжения А1 надуге радиуса .R1 ... (Начертательная геометрия и инженерная графика)
Комментарии
Оставить комментарий