Производный - понятие и значение

Рассмотрим что означает понятие и значение слова производный (информация предоставлена intellect.icu).

1. прилагательное Образованный, произведенный от чего -либо другого.

1. Образованный от другого, проистекший из чего-то другого. Вещество, производное от другого вещества. Производное слово (слово, образованное от другого слова). 2. производная, -ой, женский род В математике: величина, получающаяся в результате дифференцирования (во 2 значение ).

1. Производная, производное. 1. Произведенный, образованный от другой, простейшей или основной величины, формы, категории ( книжное ). Производная величина. Слово "паровой" - производное от "пар". 2. в значение существительное производная, ой, В высшей математике - отношение бесконечно-малого приращения зависимого переменного (функции) к бесконечно-малому приращению независимого переменного ( математика ). Скорость тела - производная от пути по времени.

-ая, -ое; -ден, -дна, -дно.

1.

Произведенный, образованный от чего -либо другого.

Производная величина. Производное слово.

В. И. Вернадский указывал: материки и океаны являются главными структурами земной коры. Все же остальные «детали» лица планеты второстепенны, они возникали и пропадали, ибо они вторичны и производны от главных струк турецкое Адабашев, Мировые загадки сегодня.

2. в значение существительное производная, -ой, женский род Мат.

Основное понятие дифференциального исчисления, характеризующее скорость изменения функции.

Часть речи

Имя прилагательное (полное)

Словоформы

производного, производному, производным, производном, производная, производной, производную, производною, производное, производные, производных, производными

Синонимы

образованный, вторичный, дериват, проистекший, исходный, паронимический

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "производный":
абажурный, абактинальный, абдикационный, абдоминальный, аберрационный, абинный, абиогенный, абиссальный, абнормальный, абонементный, боскетный, голосемянный, званый, малосемейный, несравненный, полубольный, хлебный, чебуречный, швейный

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "производный" :
рювадыный, монатяный, нилобаный, хощощеный, зявованый, рототюный, побатуный, гитононый.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Производный" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-П621, для metaphone-"прaисвaднaй" и для double-metaphone PRSF.

См. также

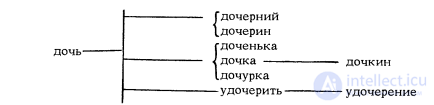... слов , давно привлекала внимание лингвистов , которые . отмечали наличие определенных связей между производными лексическими единицами и предложениями Многие слова рассматривались как трансформации определенных синтаксических конструкций ... ... для образования производных слов обусловливает . их формальную и семантическую зависимость от этих единиц и мотивированность Производные предстают как единицы , содержащие в своей структуре и семантике . отсылочную часть , повторяющую полностью ... (Лингводидактика)

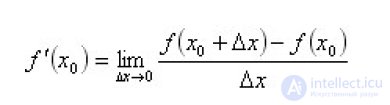... ПроизводнаяОпределение производной функции в точке : Физический смысл производной : Геометрический . смысл производной : Правила вычисления производных Уравнение касательной Таблица производных ... (СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА)

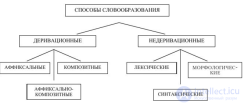... 'делать неспособным ', misdeal 'поступать неправильно .', misapply 'неправильно использовать ' и многие другие - производны Следует отметить , что смешанность ряда присуща , в основном , словам заимствованным . Анализ данных ... ... , наиболее значителен критерий содержания . Так , весьма распространено установление направления внутренней производности путем выявления семантической . зависимости одного слова от другого Если для своего семантического ... (Лингводидактика)

... переменного электрического тока основано на законе электромагнитной индукции , формулировка . которого содержит производную магнитного потока Производная в экономике :. Экономика - основа жизни , а в ней важное место ... ... скорость химической реакции через 3 секунды решение р(t) = /2 + 3 (моль ). Найдем производную функции : Р’(t) = t +3 Подставим значение t = 3 сек : P’ = 3 + 3 = 6 (моль ... (Математический анализ. Дифференциальное исчисление)

... ) Свойства функции arccosec (функция является нечетной ). Разложение в ряды для всех для всех для всех Производные от обратных тригонометрических функций Все обратные тригонометрические функции бесконечно дифференцируемы в каждой ... ... тригонометрические функции бесконечно дифференцируемы в каждой точке своей . области определения Первые производные : производные обратных тригонометрических функций Функция {\displaystyle f(x)}. Производная {\displaystyle f'(x)}. Примечание Доказательство ... (СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА)

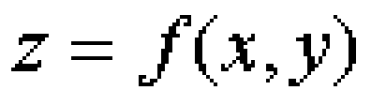... функции . Конечный предел отношения приращения функции Δzx к приращению аргумента Δx. при называется частной производной первого порядка по x и обозначается ,.т е Если считать аргумент x постоянным и рассматривать функцию как функцию ... ... функции . Конечный предел отношения приращения функции Δzy к приращению аргумента Δy. при называется частной производной первого порядка по y и обозначается ,.т е Для обозначения частных производных также используют символы ... (Математический анализ. Дифференциальное исчисление)

---

---