Тоже самое что слово - миксер,
1. Стальной сосуд для накопления расплавленного чугуна, получаемого в доменной печи и предназначенного для дальнейшей переработки (в металлургии).
2. Электрический прибор для быстрого смешивания, сбивания каких -либо продуктов.
То же, что смеситель.
МИКСЕР
{ан глагол mixer} - прибор для смешивания, сбивания чего -либо ( например , для приготовления коктейлей, муссов, сбивания сливок).
(Источник: «Словарь иностранных слов». Комлев Н.Г., 2др.- еврейское и т. п. др.- еврейское и т. п. 6)
-а, м.
1. Тех.
Сосуд для приема и накопления жидкого чугуна, получаемого в доменной печи и предназначенного для дальнейшей переработки.
2.
Электрический прибор для быстрого смешивания холодных напитков, сбивания сливок, яиц и так далее , для приготовления муссов, кремов, коктейлей и т. падеж
{Ан глагол mixer}

 ... Δ прямую , параллельную боковым . ребрам Пусть ax – отрезок этой прямой , принадлежащий призме Когда точка X описывает треугольник Δ, отрезки ax заполняют треугольную . призму Построив ... ... треугольную . призму Построив такую призму для каждого треугольника Δ, получим разбиение данной . призмы на треугольники Все эти призмы имеют одну и ту же высоту , равную . высоте ... (Стереометрия)
... Δ прямую , параллельную боковым . ребрам Пусть ax – отрезок этой прямой , принадлежащий призме Когда точка X описывает треугольник Δ, отрезки ax заполняют треугольную . призму Построив ... ... треугольную . призму Построив такую призму для каждого треугольника Δ, получим разбиение данной . призмы на треугольники Все эти призмы имеют одну и ту же высоту , равную . высоте ... (Стереометрия)
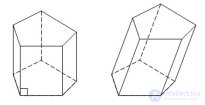 ... основаниям Призма называется наклонной , если ее боковые ребра не перпендикулярны основаниям . У прямой призмы грани – прямоугольники Призма называется правильной , если ее основания являются правильными многоугольниками Площадью ... (Стереометрия)
... основаниям Призма называется наклонной , если ее боковые ребра не перпендикулярны основаниям . У прямой призмы грани – прямоугольники Призма называется правильной , если ее основания являются правильными многоугольниками Площадью ... (Стереометрия)
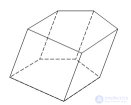 ... Призмой называется многогранник , который состоит из двух плоских многоугольников , лежащих . в разных плоскостях ... ... переносом , и всех отрезков ,.соединяющих соответствующие точки этих многоугольников Многоугольники называютсяоснованиями призмы , а отрезки , соединяющие соответствующие вершины , - боковыми ребрами . призмы Свойства призмы : Основания ... (Стереометрия)
... Призмой называется многогранник , который состоит из двух плоских многоугольников , лежащих . в разных плоскостях ... ... переносом , и всех отрезков ,.соединяющих соответствующие точки этих многоугольников Многоугольники называютсяоснованиями призмы , а отрезки , соединяющие соответствующие вершины , - боковыми ребрами . призмы Свойства призмы : Основания ... (Стереометрия)
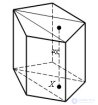
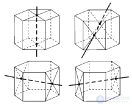 ... (рис 7 / рис 1 рис 2 Осями симметрии правильной n угольной призмы всегда являются n осей . симметрии сечения этой призмы , проходящего через середины боковых ... ... называется прямая призма , в основании которой лежит . правильный многоугольник Симметричность правильных призм определяется симметричностью их оснований (рис , а так же перпендикулярностью основаниям боковых ребер и граней ... (Стереометрия)
... (рис 7 / рис 1 рис 2 Осями симметрии правильной n угольной призмы всегда являются n осей . симметрии сечения этой призмы , проходящего через середины боковых ... ... называется прямая призма , в основании которой лежит . правильный многоугольник Симметричность правильных призм определяется симметричностью их оснований (рис , а так же перпендикулярностью основаниям боковых ребер и граней ... (Стереометрия)
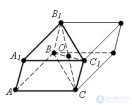 ... треугольную призму и дополним ее до параллелепипеда Точка O является центром симметрии параллелепипеда Поэтому достроенная призма симметрична исходной относительно точки O, следовательно , имеет. объем , равный объему исходной призмы ... ... его основания равна удвоенной площади треугольника ABC , а высота . равна высоте исходной призмы Отсюда заключаем , что объем исходной призмы равен произведению площади ее. основания на высоту ... (Стереометрия)
... треугольную призму и дополним ее до параллелепипеда Точка O является центром симметрии параллелепипеда Поэтому достроенная призма симметрична исходной относительно точки O, следовательно , имеет. объем , равный объему исходной призмы ... ... его основания равна удвоенной площади треугольника ABC , а высота . равна высоте исходной призмы Отсюда заключаем , что объем исходной призмы равен произведению площади ее. основания на высоту ... (Стереометрия)
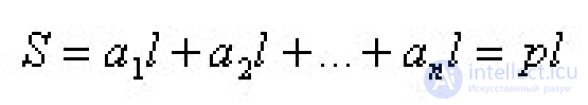 ... Теорема Боковая поверхность прямой призмы равна произведению периметра основания на. высоту призмы , т е на длину бокового ребра Доказательство Боковые грани прямой призмы – прямоугольники Основания ... ... в основании призмы ., а высоты равны длине боковых ребер Следовательно , боковая поверхность призмы равна где , , …, an – длины . ребер основания , p – периметр основания призмы , а l – длина боковых .ребер ... (Стереометрия)
... Теорема Боковая поверхность прямой призмы равна произведению периметра основания на. высоту призмы , т е на длину бокового ребра Доказательство Боковые грани прямой призмы – прямоугольники Основания ... ... в основании призмы ., а высоты равны длине боковых ребер Следовательно , боковая поверхность призмы равна где , , …, an – длины . ребер основания , p – периметр основания призмы , а l – длина боковых .ребер ... (Стереометрия)
Комментарии
Оставить комментарий