1. прилагательное Существующий в предположении.
1. Предполагаемая, предполагаемое; предполагаем, предполагема, предполагаемо ( книжное ). Прич. страдательное (причастие) прошедшее время время глагола от предполагать.
2. Существующий в предположении. Предполагаемый соперник. Предполагаемая добыча угля.
1. причастие страдательное (причастие) настоящее время от предполагать.
2. в значение прилагательное
Существующий в предположении.
Предполагаемый диагноз. Предполагаемый срок.
Вот тебе короткий расчет нашего предполагаемого раздела. Пушкин, Письмо Л. С. Пушкину, 3 июня 1836.
Остро отточенный карандаш командира дивизии обводил населенные пункты, дороги, привычно чертил стрелы предполагаемых ударов и контрударов, Поповкин, Семья Рубанюк.
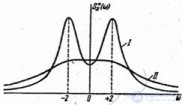... каноническим . разложением , имеем : , или, переходя к аргументу ,. , где при Придадим выражению также комплексную форму Полагая , получим : Полагая во втором интеграле , имеем :. , откуда Таким образом , мы построили ... ... и непосредственно получены из формул и. , если произвести в них замену , положить и расширить область интегрирования на интервал от до. Полагая в формуле , получим выражение дисперсии случайной функции :. Формула выражает дисперсию случайной ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
... далее , h - любой элемент из L, отличный от нулевого . вектора Тогда yn + εh L для любого ε, и поэтому , т. е Полагая получаем , что , откуда или При h = 0, неравенство также очевидно выполняется Из этого неравенства ... ... вектору Так как L замкнуто , то Переходя к пределу в неравенстве , получаем , что , и так как. h - любой элемент из подпространства L, то Полагая , получаем требуемое равенство Докажем теперь единственность этого представления Пусть , , где Тогда ... (Функциональный анализ)
... неравенствами .: a ≤ x ≤ b, φ1(x) ≤ y ≤ φ2(x),. где φ1(x), φ2(x) - функции , непрерывные на отрезке [a., b] В этом случае двойной интеграл сводится к двукратному интегралу Сначала , полагая переменную интегрирования x постоянной , находим определенный интеграл как. функцию Ф(x) переменной x. Затем находим ... (Математический анализ. Интегральное исчисление)
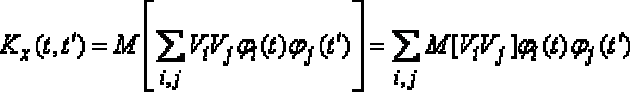... задано каноническое разложение случайной функции , то ее корреляционная функция . выражается весьма просто Полагая в формуле при , получим :. Выражение называется каноническим разложением корреляционной функции Полагая в формуле ... ... функции Выражение называется каноническим разложением корреляционной функции комплексной случайной функции Полагая в , получим выражение для дисперсии комплексной случайной функции , заданной . разложением ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
... бесконечного всемогущества Бога Мутакаллимы (сторонники калама ) отвергали причинность в материальном мире , полагая , что. единственной причиной всего , что происходит во Вселенной , является Аллах ; Аллах .не просто сотворил ... ... следовали Аристотелю Например , Разес и ал-Бируни отвергали аристотелеву теорию естественных мест , полагая ., что все частицы материи обладают тяжестью , хотя и в разной .степени ; в своем стремлении ... (Философия)
... , многие мыслители прошлого высказывали нему . скептическое отношение (от Софокла до Ницше и Фрейда ), полагая , что.лучше смотреть в лицо реальности Долгое время предполагалась , что по крайней мере в норме ... (Философия)
Комментарии
Оставить комментарий