Паребрик - понятие и значение

Рассмотрим что означает понятие и значение слова паребрик (информация предоставлена intellect.icu).

Тоже самое что слово - бордюр,

1. Полоска, обрамляющая по краю ткань, ковер и тому подобное; кайма.
2. То, что напоминает такую полоску, кайму.

Обрамляющая края цветная полоска (на обоях, материи, рисунке, лепке). 2. Невысокое обрамляющее ограждение. Б. вдоль тротуара. Цветоч- ный б. (по краям клумбы, дорожки, газона).

1. Бордюра, (фр. bordure). Полоса материи по краю чего кто-нибудь Платье с бордюром. Полоска, которой обрамляются края чего -нибудь

БОРДЮР

(франц. bordure, от bord - край). Украшение по краям чего-либо.

БОРДЮР

кайма вокруг какого-нибудь предмета (картины, стенного карниза и пр.).

БОРДЮР

украшение в виде каймы вокруг картины, по стенному карнизу, на обложке книги и так далее

БОРДЮР

франц. bordure, от bord, край. Украшение по краям чего-нибудь.

-а, м.

Полоса, которой окаймляются края ткани, обоев и т. падеж ; кайма.

Бордюр к обоям.

Мама вышивала разноцветною шерстью ковер ---; на черном фоне лилово-желтый бордюр, а в середине — рассыпные, разноцветные цветочки. Вересаев, В юные годы.

{Франц. bordure}

Синонимы

поребрик, ограждение, рама, кромка, полоса, окаймление, обрамление, бордюрчик, кайма, окантовка, каемка, окаемка, фриз, бордюр

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "паребрик":
агарик, амбарик, антропиатрик, астерик, багорик, бамберик, барик, бобрик, бодрик, брик, букварик, комбинаторик, мирик, паприк, рубрик, старик, сухарик, чирик, шарик, эксцентрик

Рифмы для этого же слова "паребрик", но если ударение на последний слог :
абажурчик, абрикосик, абрикосник, аварийщик, авиадесантник.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "паребрик" :
бабонерик, верюрорик, ыяыилорик, ризудирик, риколарик, хоьалорик, ватемерик, ломопирик.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Паребрик" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-П616, для metaphone-"парибрик" и для double-metaphone PRPR.

См. также

... в модели m, то. для обозначения этого применяется выражение , что "m выполняет α", или.что "m является моделью α". Выполнимость можно проверить , перебирая все возможные модели до тех пор ., пока не будет найдена хотя ... (Логика)

... простого числа p ≤ √m из уже найденных , отмечаем . в массиве как «непростые »; все числа кратные p, перебирая числа .с шагом в p, начиная с наименьшего кратного p числа в. данном отрезке Если число Δ выбрано ... (Алгоритмы и теория алгоритмов)

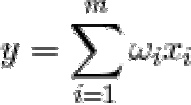... Человек , сталкиваясь с определенными задачами , придумал множество интересных нейросетевых конструкций . Эволюция , перебирая все возможные нейронные механизмы , отобрала все , что оказалось . для нее полезным Не ... (Логика мышления)

... =∟СОВ - вертикальные .Δ ВОС = по I признаку ТО III >IV ), перебираясь , каждый раз от заключения к. его основанию , происходит рассуждение по схеме : «чтобы доказать (I), надо ... (Логика)

... обозначим через. Его наименьший элемент удовлетворяет условию :. Процедура нумерации уже ясна : перебирая по указанному методу последовательно все . элементы из X, мы их выстроим в цепочку :. , где p - количество элементов ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

... , в то время как менее популярные .сервисы отображаются с более мелкими подмножествами и так далее Злоумышленник , перебирая такую схему шифрования , будет получать правдоподобные номера кредитных . карт , и типы ... (Шифры в криптографии)

---

---