математика
провести перпендикуляр на прямую из точки, лежащей вне этой прямой.

 ... Теорема Из любой точки , не лежащей на данной прямой , можно опустить . на эту прямую перпендикуляр , и только один Доказательство Пусть a - данная прямая и не ... ... b проходила через точку A Тогда прямая b ⊥ a, так как b || с и с. ⊥ a Значит отрезок AB ⊥ a Теперь докажем единственность перпендикуляра AB Допустим , существует еще перпендикуляр , проходящий через точку A к прямой . a Тогда у треугольника ... (Планометрия)
... Теорема Из любой точки , не лежащей на данной прямой , можно опустить . на эту прямую перпендикуляр , и только один Доказательство Пусть a - данная прямая и не ... ... b проходила через точку A Тогда прямая b ⊥ a, так как b || с и с. ⊥ a Значит отрезок AB ⊥ a Теперь докажем единственность перпендикуляра AB Допустим , существует еще перпендикуляр , проходящий через точку A к прямой . a Тогда у треугольника ... (Планометрия)
 ... точку , не лежащую на данной прямой , МОЖНО провести прямую ., параллельную данной Опустив перпендикуляр из точки на прямую , а затем , восставив перпендикуляр . к проведенной прямой , получим две ... ... прямые , перпендикулярные . третьей , параллельны между собой Из середины отрезка секущей опускают перпендикуляр на одну из параллельных . прямых Затем перпендикуляр продляют до пересечения со второй прямой Из ... (Планометрия)
... точку , не лежащую на данной прямой , МОЖНО провести прямую ., параллельную данной Опустив перпендикуляр из точки на прямую , а затем , восставив перпендикуляр . к проведенной прямой , получим две ... ... прямые , перпендикулярные . третьей , параллельны между собой Из середины отрезка секущей опускают перпендикуляр на одну из параллельных . прямых Затем перпендикуляр продляют до пересечения со второй прямой Из ... (Планометрия)
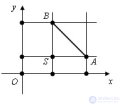 ... Даны две точки A (; y и B (; y. Найдем расстояние между точками A и B Опустим перпендикуляры из точек A и B на ось абсцисс . и на ось ординат Как видно из рисунка , пара ... ... перпендикуляры из точек A и B на ось абсцисс . и на ось ординат Как видно из рисунка , пара перпендикуляров пересекаются в точке S. Расстояние между точками B и S равно ||, а расстояние . между точками S и A равно ||. Получаем треугольник ... (Планометрия)
... Даны две точки A (; y и B (; y. Найдем расстояние между точками A и B Опустим перпендикуляры из точек A и B на ось абсцисс . и на ось ординат Как видно из рисунка , пара ... ... перпендикуляры из точек A и B на ось абсцисс . и на ось ординат Как видно из рисунка , пара перпендикуляров пересекаются в точке S. Расстояние между точками B и S равно ||, а расстояние . между точками S и A равно ||. Получаем треугольник ... (Планометрия)
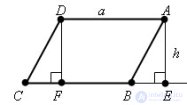 ... параллелограмм Если он не является прямоугольником , то один из его углов . A или B острый Пусть для определенности A острый Опустим перпендикуляр AE из вершины A на прямую CB Площадь трапеции AECD равна сумме ... ... Площадь трапеции AECD равна сумме площадей параллелограмма ABCD и треугольника . AEB Опустим перпендикуляр DF из вершины D на прямую CD Тогда площадь трапеции AECD равна ... (Планометрия)
... параллелограмм Если он не является прямоугольником , то один из его углов . A или B острый Пусть для определенности A острый Опустим перпендикуляр AE из вершины A на прямую CB Площадь трапеции AECD равна сумме ... ... Площадь трапеции AECD равна сумме площадей параллелограмма ABCD и треугольника . AEB Опустим перпендикуляр DF из вершины D на прямую CD Тогда площадь трапеции AECD равна ... (Планометрия)
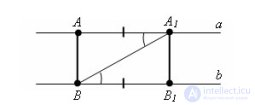 ... до параллельной прямой равны . Пусть а и b – параллельные прямые и точки A и. – некоторые точки на прямой a Опустим из точки A перпендикуляр AB на прямую b и. отложим из точки B отрезок , равный так, что.бы A и были по разные ... ... треугольников (. – общая , ∠ = ∠ – как внутренние накрест лежащие , =). Из равенства треугольников следует , что тоже перпендикуляр к прямой . b и AB = Теорема доказана Расстоянием между параллельными прямыми называется расстояние от какой-нибудь ... (Планометрия)
... до параллельной прямой равны . Пусть а и b – параллельные прямые и точки A и. – некоторые точки на прямой a Опустим из точки A перпендикуляр AB на прямую b и. отложим из точки B отрезок , равный так, что.бы A и были по разные ... ... треугольников (. – общая , ∠ = ∠ – как внутренние накрест лежащие , =). Из равенства треугольников следует , что тоже перпендикуляр к прямой . b и AB = Теорема доказана Расстоянием между параллельными прямыми называется расстояние от какой-нибудь ... (Планометрия)
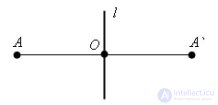 ... , что фигура обладает осевой симметрией Есть прямая l и точка A не лежащая на прямой . Опустим из точки A на прямую l перпендикуляр На продолжении этого перпендикуляра отложим отрезок OA ... (Планометрия)
... , что фигура обладает осевой симметрией Есть прямая l и точка A не лежащая на прямой . Опустим из точки A на прямую l перпендикуляр На продолжении этого перпендикуляра отложим отрезок OA ... (Планометрия)
Комментарии
Оставить комментарий