Накрасть - понятие и значение

Рассмотрим что означает понятие и значение слова накрасть (информация предоставлена intellect.icu).

1. Сов. переходный смотрите накрадывать

1. Накраду, накрадёшь, прошедшее время накрал, совершенный вид (к накрадывать), что и чего. Добыть путем краж, наворовать.

-краду, -крадёшь; прошедшее время накрал, -ла, -ло; причастие страдательное (причастие) прошедшее время накраденный,

-ден, -а, -о; совершенный вид , переходный (что и чего)

( несовершенный вид накрадывать).

Добыть путем краж в каком -либо (обычно большом) количестве; наворовать.

Накрасть денег.

{Дубровин:} Добра чужого Награблено, накрадено довольно. А. Островский, Воевода.

Часть речи

Глагол (инфинитив)

Синонимы

похищенный, присвоенный, натаскавший, наворовавший, наворованный, натащивший, стибривший, натыренный, натибренный, награбивший, присвоивший, награбаставший, натыривший, понаворовавший, надыбавший, нагайдаривший, надыбивший, натараканивший, своровавший, свистнувший, стыривший, слямзивший, стянувший, стащивший, похитивший, укравший, сбондивший, подтибривший, слимонивший, сперший

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "накрасть":
абсолютность, абстрактность, абсурдность, авантажность, авантюрность, аварийность, авиачасть, автентичность, автобиографичность, автоматичность, есть, напасть, пасть, прелесть, странность, субтильность, утонченность, утончённость, учтивость, часть

Рифмы для этого же слова "накрасть", но если ударение на последний слог :
аббатствовать, абдуцировать, абецедировать, аблактировать, абонировать.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "накрасть" :
тасыдость, ниринесть, нукевасть, киьоыесть, нймагисть, човепость, месунисть, ыоланисть.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Накрасть" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-Н262, для metaphone-"накраст" и для double-metaphone NKRS.

См. также

... , то углы KBA и MAB называются внутренними накрест .лежащими Если у пары внутренних накрест лежащих углов ( угол 1 и. угол один из углов заменить на вертикальный ему ... ... пары которых имеют . особые названия и свойства :. Соответственные углы равны (Рис . Накрест лежащие углы равны (Рис . Внутренние односторонние углы в сумме составляют 180 ... (Планометрия)

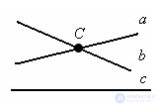... А так как через точку A можно провести только одну . прямую параллельную b, то a и совпадают Значит , внутренние накрест лежащие углы , образованные прямой a и b., равны Теорема доказана На основании теоремы ... ... . b в точке B Проведем чрез точку A прямую так, что бы прямые . и b с секущей с образовали равные внутренние накрест .лежащие углы По признаку параллельности прямых прямые и b параллельны А так как через точку A можно ... (Планометрия)

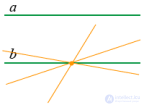... a || b, то ∠2 = ∠. При пересечении двух параллельных прямых третьей прямой , образованные ими накрест . лежащие углы равны : Если a || b, то ∠1 = ∠. Следующее свойство является частным случаем для каждого ... ... соответственные углы равны , то прямые параллельны :. Если ∠2 = ∠4 , то a || b Если внутренние накрест лежащие углы равны , то прямые параллельны :. Если ∠1 = ∠3 , то a || b Свойства параллельных ... (Планометрия)

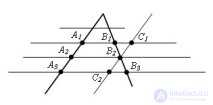... .и По свойствам параллелограмма , = и = Так . как = , то = Δ = Δ.по второму признаку равенства треугольников ( = , ∠ = ∠ , как вертикальные ., ∠ = ∠ = , как внутренние накрест лежащие при прямых и. и секущей Из равенства треугольников следует , что =. Теорема доказана ... (Планометрия)

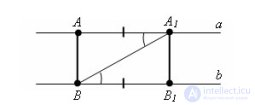... так, что.бы A и были по разные стороны от прямой . Δ = Δ по первому признаку равенства треугольников (. – общая , ∠ = ∠ – как внутренние накрест лежащие , =). Из равенства треугольников следует , что тоже перпендикуляр к прямой . b и AB = Теорема ... (Планометрия)

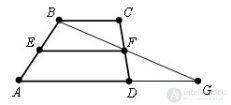... по второму признаку равенства треугольников (CF . = FD , по построению , ∠ BCF = ∠ ПВА , как внутренние накрест лежащие при.параллельных прямых ВС и DG и секущей CD , ∠ CFB = ∠ DFG , как. вертикальные ... (Планометрия)

---

---