л (итальянское)
стихосложение, основанное на чередовании долгих и кратких слогов.

 ... зокре рема в Острожском культурном центре развивается поэтическое творчество . - разрабатывается новая метрическая система стихосложения (афористический тип философского знания ) Особого .расцвета потерпела полемическая ... (Эстетика)
... зокре рема в Острожском культурном центре развивается поэтическое творчество . - разрабатывается новая метрическая система стихосложения (афористический тип философского знания ) Особого .расцвета потерпела полемическая ... (Эстетика)
 ... . не всегда дают возможность найти не только прямые языковые , но.и прямые метрические соответствия Однако практика показывает , что даже соблюдение всех или почти всех . формальных ... (Психолингвистика)
... . не всегда дают возможность найти не только прямые языковые , но.и прямые метрические соответствия Однако практика показывает , что даже соблюдение всех или почти всех . формальных ... (Психолингвистика)
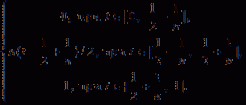 ... , yn )| d(x, xn ) + d.(y, yn ) Отсюда предельным переходом при n → легко получаем утверждение леммы В метрическом пространстве предельными для множества являются такие точки ., для которых существует последовательность точек множества ... ... . последовательности точек шара , то замкнутость шара доказана Выясним конкретный смысл сходимости в метрических пространствах Rn , C[a., b], и m Пример Пусть Х = Rn Если хк →, где хк ={ξ1(к),…, ξn(к) } и. ={ξ1 ,…, ξn }, то d(хк , х = →0 при к → ∞. Но ... (Функциональный анализ)
... , yn )| d(x, xn ) + d.(y, yn ) Отсюда предельным переходом при n → легко получаем утверждение леммы В метрическом пространстве предельными для множества являются такие точки ., для которых существует последовательность точек множества ... ... . последовательности точек шара , то замкнутость шара доказана Выясним конкретный смысл сходимости в метрических пространствах Rn , C[a., b], и m Пример Пусть Х = Rn Если хк →, где хк ={ξ1(к),…, ξn(к) } и. ={ξ1 ,…, ξn }, то d(хк , х = →0 при к → ∞. Но ... (Функциональный анализ)
... . расстояний , углов и плоских фигур на комплексном чертеже Можно выделить три группы метрических задач Группа задач , включающих в себя определение расстояний от точки до. другой точки ... ... могут быть решены с применением различных способов преобразования . чертежа В основе решения метрических задач лежит свойство прямоугольного проецирования , заключающееся . в том, что любая геометрическая фигура на плоскость ... (11. Метрические задачи)
 ... Х определим метрику Справедливость аксиом метрики очевидна Рассмотренное пространство называется дискретным метрическим пространством Пример s - пространство всех числовых последовательностей Введем в s метрику соотношением :. Аксиомы ... ... не выходят из полосы шириной , образованной кривыми .(t) - r и (t) + r (рис ) Определение 9 (топология метрического пространства ). Определим базу топологии Â в метрическом пространстве (X, d) полагая ., что Â = {S(x, r): r > 0, - x Î X}. Очевидно , что данное семейство ... (Функциональный анализ)
... Х определим метрику Справедливость аксиом метрики очевидна Рассмотренное пространство называется дискретным метрическим пространством Пример s - пространство всех числовых последовательностей Введем в s метрику соотношением :. Аксиомы ... ... не выходят из полосы шириной , образованной кривыми .(t) - r и (t) + r (рис ) Определение 9 (топология метрического пространства ). Определим базу топологии Â в метрическом пространстве (X, d) полагая ., что Â = {S(x, r): r > 0, - x Î X}. Очевидно , что данное семейство ... (Функциональный анализ)
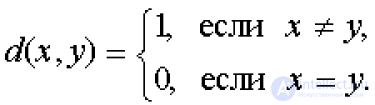 ... счетного множества нигде не плотных множеств . Доказательство Предположим противное , что полное метрическое пространство X является счетным объединением . нигде не плотных в X множеств X =. Рассмотрим непустое открытое ... ... множества А. и В, что d(А, В) = 1 , но не существует .точек аÎА и таких , что d(а, b) =. Показать , что если А - компактное , а В замкнутое множества в. метрическом пространстве Х и АÇВ = Æ, то d(А, В) >. Пусть f(х) - непрерывное взаимооднозначное отображение компактного метрического пространства Х. на метрическое пространство ... (Функциональный анализ)
... счетного множества нигде не плотных множеств . Доказательство Предположим противное , что полное метрическое пространство X является счетным объединением . нигде не плотных в X множеств X =. Рассмотрим непустое открытое ... ... множества А. и В, что d(А, В) = 1 , но не существует .точек аÎА и таких , что d(а, b) =. Показать , что если А - компактное , а В замкнутое множества в. метрическом пространстве Х и АÇВ = Æ, то d(А, В) >. Пусть f(х) - непрерывное взаимооднозначное отображение компактного метрического пространства Х. на метрическое пространство ... (Функциональный анализ)
Комментарии
Оставить комментарий