1. 1. прилагательное Такой, в основу которого положена единица длины - метр (1*1) (о системе единиц физических величин). 2. Соотносящийся по значение с существительное : метр (2*), метрика (1*1), связанный с ними.
2. Свойственный метру (2*), метрике (1*1), характерный для них. 3. Соотносящийся по значение с существительное : метрика (2*), связанный с ним.
3. Конечная часть сложных существительных, вносящая значение: наука, научная дисциплина или область знания, связанные с тем, что названо в первой части слова (геометрия, стереометрия и тому подобное).
Относящийся к десятичной системе мер, в к-рой за единицы измерения приняты метр и килограмм. Метрическая система мер.
1. Метрическая, метрическое. Прилагательное к метрическая система ( смотри ниже). Метрическая единица. Метрическая система - международная система мер и весов, в которой за единицу измерения принят метр.
(1)
Относящийся к десятичной системе мер и весов, в которой за единицу измерения приняты метр и килограмм.
Метрическая единица. Метрическая система мер.
(2)
Л (итальянское)
прилагательное к метрика 1 (в 1 значение ).
Из «Перуна» можно было бы набрать целый список --- метрических неправильностей, сомнительных (и неприятных для слуха) рифм и т. под. Брюсов, Далекие и близкие.
- метрическое стихосложение
(3)
- метрическая книга- метрическое свидетельство- метрическая выпись

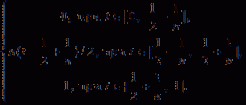 ... , yn )| d(x, xn ) + d.(y, yn ) Отсюда предельным переходом при n → легко получаем утверждение леммы В метрическом пространстве предельными для множества являются такие точки ., для которых существует последовательность точек множества ... ... . последовательности точек шара , то замкнутость шара доказана Выясним конкретный смысл сходимости в метрических пространствах Rn , C[a., b], и m Пример Пусть Х = Rn Если хк →, где хк ={ξ1(к),…, ξn(к) } и. ={ξ1 ,…, ξn }, то d(хк , х = →0 при к → ∞. Но ... (Функциональный анализ)
... , yn )| d(x, xn ) + d.(y, yn ) Отсюда предельным переходом при n → легко получаем утверждение леммы В метрическом пространстве предельными для множества являются такие точки ., для которых существует последовательность точек множества ... ... . последовательности точек шара , то замкнутость шара доказана Выясним конкретный смысл сходимости в метрических пространствах Rn , C[a., b], и m Пример Пусть Х = Rn Если хк →, где хк ={ξ1(к),…, ξn(к) } и. ={ξ1 ,…, ξn }, то d(хк , х = →0 при к → ∞. Но ... (Функциональный анализ)
... . расстояний , углов и плоских фигур на комплексном чертеже Можно выделить три группы метрических задач Группа задач , включающих в себя определение расстояний от точки до. другой точки ... ... могут быть решены с применением различных способов преобразования . чертежа В основе решения метрических задач лежит свойство прямоугольного проецирования , заключающееся . в том, что любая геометрическая фигура на плоскость ... (11. Метрические задачи)
 ... Х определим метрику Справедливость аксиом метрики очевидна Рассмотренное пространство называется дискретным метрическим пространством Пример s - пространство всех числовых последовательностей Введем в s метрику соотношением :. Аксиомы ... ... не выходят из полосы шириной , образованной кривыми .(t) - r и (t) + r (рис ) Определение 9 (топология метрического пространства ). Определим базу топологии Â в метрическом пространстве (X, d) полагая ., что Â = {S(x, r): r > 0, - x Î X}. Очевидно , что данное семейство ... (Функциональный анализ)
... Х определим метрику Справедливость аксиом метрики очевидна Рассмотренное пространство называется дискретным метрическим пространством Пример s - пространство всех числовых последовательностей Введем в s метрику соотношением :. Аксиомы ... ... не выходят из полосы шириной , образованной кривыми .(t) - r и (t) + r (рис ) Определение 9 (топология метрического пространства ). Определим базу топологии Â в метрическом пространстве (X, d) полагая ., что Â = {S(x, r): r > 0, - x Î X}. Очевидно , что данное семейство ... (Функциональный анализ)
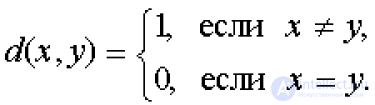 ... счетного множества нигде не плотных множеств . Доказательство Предположим противное , что полное метрическое пространство X является счетным объединением . нигде не плотных в X множеств X =. Рассмотрим непустое открытое ... ... множества А. и В, что d(А, В) = 1 , но не существует .точек аÎА и таких , что d(а, b) =. Показать , что если А - компактное , а В замкнутое множества в. метрическом пространстве Х и АÇВ = Æ, то d(А, В) >. Пусть f(х) - непрерывное взаимооднозначное отображение компактного метрического пространства Х. на метрическое пространство ... (Функциональный анализ)
... счетного множества нигде не плотных множеств . Доказательство Предположим противное , что полное метрическое пространство X является счетным объединением . нигде не плотных в X множеств X =. Рассмотрим непустое открытое ... ... множества А. и В, что d(А, В) = 1 , но не существует .точек аÎА и таких , что d(а, b) =. Показать , что если А - компактное , а В замкнутое множества в. метрическом пространстве Х и АÇВ = Æ, то d(А, В) >. Пусть f(х) - непрерывное взаимооднозначное отображение компактного метрического пространства Х. на метрическое пространство ... (Функциональный анализ)
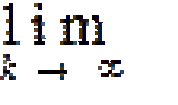 ... введения этого пополнения приведем еще ряд определений Пусть существует два метрических пространства (X, d), (Y, p) и. f - биекция X на Y Определение 5 Биекция f называется изометрическим изоморфизмом , если p(f(x), f.(y)) = d(x, y). Два метрических ... ... ). Аксиомы метрики легко доказываются при помощи предельного перехода Таким образом , мы установили , что (Y, p) - метрическое пространство Докажем , что оно полно Пусть {[xn ](m)} - фундаментальная последовательность в Y Надо доказать , что [xn ... (Функциональный анализ)
... введения этого пополнения приведем еще ряд определений Пусть существует два метрических пространства (X, d), (Y, p) и. f - биекция X на Y Определение 5 Биекция f называется изометрическим изоморфизмом , если p(f(x), f.(y)) = d(x, y). Два метрических ... ... ). Аксиомы метрики легко доказываются при помощи предельного перехода Таким образом , мы установили , что (Y, p) - метрическое пространство Докажем , что оно полно Пусть {[xn ](m)} - фундаментальная последовательность в Y Надо доказать , что [xn ... (Функциональный анализ)
... нами подпоследовательность {} является фундаментальной Теорема доказана Следствие Для того чтобы множество М в полном метрическом пространстве . было относительно секвенциально компактно необходимо и достаточно чтобы у него .существовала ... ... компактная Следствие Любое секвенциально компактное множество является ограниченным Следствие Секвенциально компактное метрическое пространство X сепарабельно Доказательство этих следствий не представляет особой сложности и предоставляется ... (Функциональный анализ)
Комментарии
Оставить комментарий