Либечио - понятие и значение

Рассмотрим что означает понятие и значение слова либечио (информация предоставлена intellect.icu).

ЛИБЕЧИО

итал. libeccio. Юго-западный ветер в Нижней Италии.

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "либечио":
бамбочио, бароччио, варначио, кальчио, каприччио, либеччио, пальячио, пастичио, скарамуччио

Рифмы для этого же слова "либечио", но если ударение на последний слог :
агио, адажио, ажио, анабио, ангио.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "либечио" :
гокарычио, тенюмучио, тичеыачио, пыреьечио, рякеночио, дотежачио, тасилачио, буридочио.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Либечио" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-Л120, для metaphone-"либичиa" и для double-metaphone primary : LPX secondary: LPK.

См. также

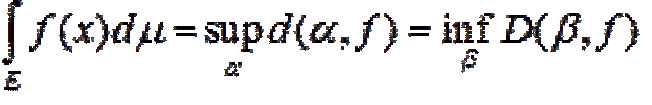... определения связано с числами А и В,.на самом деле от них не зависит Теорема Если l ® 0, то суммы Лебега s и S. стремятся к интегралу Теорема непосредственно вытекает из неравенств ... ... на оси Ох ., а по признаку достаточной близости соответствующих значений функции С этой целью Лебег разбивает на части не отрезок [a., b], расположенный на оси абсцисс , а отрезок [А, В], лежащий .на оси ... (Функциональный анализ)

... изоморфизм , 28 изоморфизм конечномерных пространств , 110 индуцированная топология , 18 интеграл Лебега от неотрицательной функции , 86 интеграл Лебега от ограниченной функции , 80 интеграл Лебега ... (Функциональный анализ)

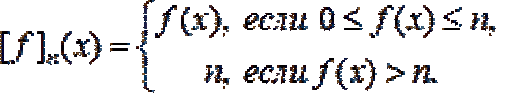... не нулевые значения должна быть .конечной Установим некоторые свойства интеграла Лебега от простых функций A) = + Для доказательства предположим , что f принимает значения fi на множествах . Fi ... ... =k (проверяется непосредственно . ) Лемма 3 позволяет на самом деле подойти к определению интеграла . Лебега от неотрицательных измеримых функций еще с одной стороны Теорема Интеграл Лебега от неотрицательной ... (Функциональный анализ)

... m() ³ с + l. > c Этим показано , что [a, b]Ç( - d, + d.) Ì [a, b]Ç{m(x) > c} и множество [a,.b]Ç{m(x) > c} является открытым в [a, b], а. значит и измеримым Этим показано , что одно из множеств Лебега нижней функции Бэра . измеримо и, следовательно , сама функция измерима Теорема 17 ... ... нижней функции Бэра . измеримо и, следовательно , сама функция измерима Теорема 17 (Лебег ). Для того чтобы ограниченная функция f(x) была интегрируема (R.) на отрезке [a, b], необходимо и достаточно , чтобы ... (Функциональный анализ)

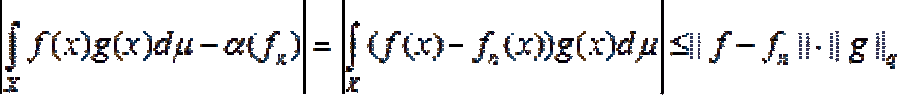... пространству Lq (X), где. число q = p/(p- в случае 1 < р < ¥ и q = ¥.в случае р = При этом каждый ограниченный функционал aÎ *(X.) представляется интегралом Лебега : , где g Î Lq (X) и норма функционала равна ||a.|| = ||g||q (норме функции g в пространстве Lq (X)). Доказательство Рассмотрим ... ... ., то она является равномерным пределом последовательности простых функций hn ÎÁ(.Х) Поэтому = Откуда и из определения интеграла Лебега вытекает , что ||g||q. £ ||a|| в случае р >. В случае р = 1 допустим , что при некотором e > 0. множество Е Ì{xÎA: |g(x)| > ||a|| + e} имеет конечную .и положительную меру Полагая h(х) = cE ... (Функциональный анализ)

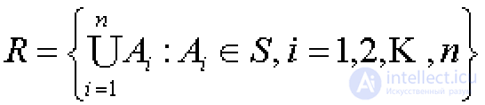... (теорема Мера , порожденная этой внешней . мерой на множествах из Rn называется мерой Лебега на Rn Следующая теорема является аналогом ранее доказанной теоремы о структуре открытых . множеств ... (Функциональный анализ)

---

---