Гиперболический - понятие и значение

Рассмотрим что означает понятие и значение слова гиперболический (информация предоставлена intellect.icu).

1. Соотносящийся по значение с существительное : гипербола (1*), связанный с ним.
2. Свойственный гиперболе (1*), характерный для нее.
3. Насыщенный гиперболами. 2. Соотносящийся по значение с существительное : гипербола (2*), связанный с ним.
4. Свойственный гиперболе (2*), характерный для нее.

1. Гиперболическая, гиперболическое (в качестве краткая форма прилагательного форм употребляется, употребляющийся гиперболичен, гиперболична, гиперболично). 1. только полная форма прилагательного формы. Прилагательное к гипербола ( математика ). Гиперболическое сечение. 2. только полная форма прилагательного формы. Представляющий собой гиперболу, обильный гиперболами (л (итальянское) ). Гиперболический стиль. Гиперболическое сравнение. 3. То же, что гиперболичный ( книжное ). Гиперболический ужас.

ГИПЕРБОЛИЧЕСКИЙ

(от гипербола). Преувеличенный.

ГИПЕРБОЛИЧЕСКИЙ

от слова гипербола. Преувеличенный.

(1)

Представляющий собой гиперболу1; обильный гиперболами.

Гиперболический стиль. Гиперболическое сравнение.

Преувеличенный.

Во всех {созданиях Державина} воображение преобладает над чувством и все представляется в преувеличенных, гиперболических размерах. Белинский, Литературные мечтания.

(2)

Мат.

прилагательное к гипербола 2.

Гиперболическое сечение.

Часть речи

Имя прилагательное (полное)

Словоформы

гиперболического, гиперболическому, гиперболическим, гиперболическом, гиперболическая, гиперболической, гиперболическую, гиперболическою, гиперболическое, гиперболические, гиперболических, гиперболическими

Синонимы

радиогиперболический, раздутый, преувеличенный, гиперболизированный, дутый, утрированный, гиперболичный

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "гиперболический":
абазинский, аббатский, абверовский, абдеристический, абиссинский, аболиционистский, абонентский, абсолютистский, абстракционистский, абхазский, венгерский, высокий, героический, горнозаводский, горький, жидкий, лёгкий, психический, щегольский

Рифмы для этого же слова "гиперболический", но если ударение на последний слог :
абецедарий.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "гиперболический" :
хикококий, башевокий, тинйсэкий, ьачэлакий, ьасонокий, нонатикий, ритенакий, зоносекий.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Гиперболический" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-Г161, для metaphone-"гипирбaличиский" и для double-metaphone primary : JPRP secondary: KPRP.

См. также

... комплексного логарифма Радиус сходимости обоих рядов равен Связь с обратными тригонометрическими и гиперболическими функциями [править ]. Поскольку комплексные тригонометрические функции связаны с экспонентой (формула Эйлера ... ... Эйлера ), то. комплексный логарифм как обратная к экспоненте функция связан собратными тригонометрическими .функциями : Гиперболические функции на комплексной плоскости можно рассматривать как тригонометрические функции . мнимого аргумента , поэтому ... (Комплексный анализ и операционное исчисление (теория функций комплексного переменного))

... , которые встречаются под равными углами .больше 90 ° Противоположные дуги равны по длине В гиперболической геометрии , гиперболической прямоугольник представляет собой фигуру в гиперболической . плоскости , четыре ребра ... ... геометрии , гиперболической прямоугольник представляет собой фигуру в гиперболической . плоскости , четыре ребра гиперболические дуги , которые встречаются под равными углами .менее 90 ° Противоположные дуги равны ... (Планометрия)

... функций Дифференциальный бином («длинный логарифм »;) Доказательство Пусть , предположим также , что Воспользуемся гиперболическими функциями , сделаем замену . Но Поэтому Отсюда , включая логарифм знаменателя последней ... ... интегралов от тригонометрических функций , список интегралов от обратных тригонометрических . функций Доказательство Доказательство Гиперболические функции Список интегралов от гиперболических функций также также Доказательства Доказательство формулы ... (Математический анализ. Интегральное исчисление)

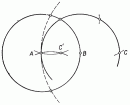... (в этом случае уравнение не .определяет на плоскости никакого геометрического образа ). При Δ ... (3 Некоторые геометрические построения)

... - частица «движется »; внутри . барьера с «мнимым »; волновым вектором В этом случае тригонометрическая функция перейдет в гиперболическую и из уравнения следует выражение для коэффициента прохождения Если , как это обычно бывает , аргумент то доминирует ... (Атомная и Ядерная физика)

... активационные . функции с неоднородностями не подходят для рассматриваемых НС В них применяются такие гладкие функции , как гиперболический тангенс или. классический сигмоид с экспонентой В случае гиперболического тангенса Третий множитель ¶sj /¶wij ... ... // отображения слоев на экране SetSigmoidType (HYPERTAN );// задание вида активационной функции // HYPERTAN - гиперболический тангенс (рекомедуется ). // ORIGINAL - сигмоид SetNiuParm ; // коэфициент обучения сети лежит в интервале ... (Модели и методы исследований)

---

---