Нареч. Везде, повсеместно.это наречие, которое описывает распространение или наличие чего-либо во всех местах или повсюду. Это может означать, что что-то присутствует во всех местах одновременно или что оно наблюдается во всех возможных направлениях или ситуациях.
Термин "везде" используется в различных контекстах. Например, в фразе "Он везде" может означать, что человек очень активен и присутствует во всех местах или во всех социальных кругах. В техническом смысле, "везде" может относиться к концепции всюдуналичия (Ubiquitous Computing), когда вычислительные возможности встроены во все объекты и окружают нас повсюду, так что мы можем получить доступ к информации и функциям в любое время и в любом месте.
Однако без более конкретного контекста нельзя дать более точного определения "везде". Если у вас есть конкретный вопрос или контекст, пожалуйста, уточните его, и я буду рад помочь вам.
Во всех местах, везде или в разные, во все места. В. побывал. В. сует свой нос.
1. Нареч. Везде, повсеместно.
наречие
Везде, повсеместно.
{Треплев:} Куда бы я ни смотрел, всюду мне представляется ваше лицо, эта ласковая улыбка. Чехов, Чайка.
Всюду стоял едкий, незнакомый запах. М. Горький, Детство.

 ... и последовательность . fn (x) Þ f(x) на X Тогда существует такая возрастающая последовательность натуральных чисел {nk }, что ® f.(x) при п ® ¥ почти всюду на X Доказательство Сначала предположим , что m(Х) < ¥. Возьмем = 1 и для k = 1 , 2 ,. выберем натуральное > - 1 ... ... так, чтобы В силу сходимости по мере такая последовательность индексов найдется Докажем , что последовательность ® f(x) почти всюду на X Действительно , если заданы e > 0 и d > 0, то подберем . так, чтобы и Тогда при т> имеем Применяя теорему 3 , убеждаемся ... (Функциональный анализ)
... и последовательность . fn (x) Þ f(x) на X Тогда существует такая возрастающая последовательность натуральных чисел {nk }, что ® f.(x) при п ® ¥ почти всюду на X Доказательство Сначала предположим , что m(Х) < ¥. Возьмем = 1 и для k = 1 , 2 ,. выберем натуральное > - 1 ... ... так, чтобы В силу сходимости по мере такая последовательность индексов найдется Докажем , что последовательность ® f(x) почти всюду на X Действительно , если заданы e > 0 и d > 0, то подберем . так, чтобы и Тогда при т> имеем Применяя теорему 3 , убеждаемся ... (Функциональный анализ)
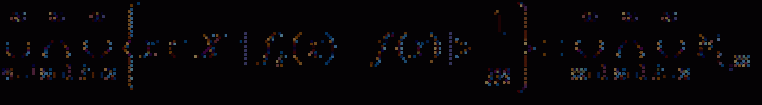 ... по существу в ходе доказательства теоремы Определение Последовательность функций {fn } сходится почти всюду (п в ) к функции f на множестве Е, если существует такое множество . меры нуль m(А) = 0, что справедливо равенство f(.x) = при всех ... ... , на самом .деле , являются классы эквивалентных функций Нетрудно проверить , что предел f(x) = почти всюду сходящейся последовательности . измеримых функций является также измеримой функцией и определяется однозначно с.точностью ... (Функциональный анализ)
... по существу в ходе доказательства теоремы Определение Последовательность функций {fn } сходится почти всюду (п в ) к функции f на множестве Е, если существует такое множество . меры нуль m(А) = 0, что справедливо равенство f(.x) = при всех ... ... , на самом .деле , являются классы эквивалентных функций Нетрудно проверить , что предел f(x) = почти всюду сходящейся последовательности . измеримых функций является также измеримой функцией и определяется однозначно с.точностью ... (Функциональный анализ)
... множества , 15 внутренняя точка множества , 15 вполне непрерывный оператор , 173 всюду плотное подмножество , 28 вторая итерация ядра , 139 вторая теорема Фредгольма ... (Функциональный анализ)
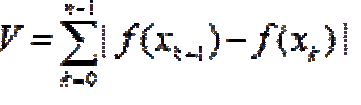 ... интегрируемая функция на Е и mE .{ f (x) ³ c} = a Доказать , что Пусть f (x) - интегрируемая на [a, b] функция Доказать , что если при любом c Î[a, b], то. f (x) = 0 почти всюду на [a, b]. Интегрируемы ли по Лебегу функции 1 /х и 1 /. на интервале (0, Пусть ограниченная функция f (x) интегрируема ... ... на (a, b). Пусть - последовательность измеримых на Е ограниченных неотрицательных функций Пусть ® 0 при n ® ¥. Следует ли из этого , что fn (x) ® 0 при n. ® ¥ всюду или хотя бы почти всюду на Е Построить на каком-либо множестве Е конечной меры последовательность ограниченных ... (Функциональный анализ)
... интегрируемая функция на Е и mE .{ f (x) ³ c} = a Доказать , что Пусть f (x) - интегрируемая на [a, b] функция Доказать , что если при любом c Î[a, b], то. f (x) = 0 почти всюду на [a, b]. Интегрируемы ли по Лебегу функции 1 /х и 1 /. на интервале (0, Пусть ограниченная функция f (x) интегрируема ... ... на (a, b). Пусть - последовательность измеримых на Е ограниченных неотрицательных функций Пусть ® 0 при n ® ¥. Следует ли из этого , что fn (x) ® 0 при n. ® ¥ всюду или хотя бы почти всюду на Е Построить на каком-либо множестве Е конечной меры последовательность ограниченных ... (Функциональный анализ)
 ... Доказательство Так как Γ - нечеткий гомоморфизм , то Γ - нечеткое отображение X. в Y и по определению оно является нечетким функциональным и.нечетким всюду определенным соответствием Известно , что, если Γ - нечеткое функциональное и всюду определенное соответствие ., то его инверсия обладает ... ... и из того, что Γ и Γ-1 - нечеткие гомоморфизмы ., вытекает , что Γ и Γ-1 - одно -. временно нечеткие функциональные , нечеткие инъективные , нечеткие всюду определенные и нечеткие . сюръективные , т е нечеткие биективные соответствия Следовательно , Γ и Γ-1 - нечеткие изоморфизмы Теорема ... (Вычислительный интеллект)
... Доказательство Так как Γ - нечеткий гомоморфизм , то Γ - нечеткое отображение X. в Y и по определению оно является нечетким функциональным и.нечетким всюду определенным соответствием Известно , что, если Γ - нечеткое функциональное и всюду определенное соответствие ., то его инверсия обладает ... ... и из того, что Γ и Γ-1 - нечеткие гомоморфизмы ., вытекает , что Γ и Γ-1 - одно -. временно нечеткие функциональные , нечеткие инъективные , нечеткие всюду определенные и нечеткие . сюръективные , т е нечеткие биективные соответствия Следовательно , Γ и Γ-1 - нечеткие изоморфизмы Теорема ... (Вычислительный интеллект)
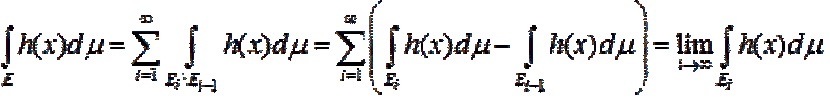 ... на измеримом множестве E. задана последовательность измеримых функций (x), (x), (x), ¼ , fn (x), ¼. которая в каком-нибудь смысле (всюду , почти всюду , по мере ) сходится . к измеримой функции F(x). Спрашивается , будет ли справедливо соотношение ... (Функциональный анализ)
... на измеримом множестве E. задана последовательность измеримых функций (x), (x), (x), ¼ , fn (x), ¼. которая в каком-нибудь смысле (всюду , почти всюду , по мере ) сходится . к измеримой функции F(x). Спрашивается , будет ли справедливо соотношение ... (Функциональный анализ)
Комментарии
Оставить комментарий