Арифметическая прогрессия - понятие и значение

Рассмотрим что означает понятие и значение слова арифметическая прогрессия (информация предоставлена intellect.icu).

АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ

ряд чисел, в котором разность между членами любой пары одна и та же; нпр., восходящая а. пр. 2, 7, 12, 17, 22, 27 и так далее , нисходящая 1др.- еврейское и т. п. , 8, 6, 4, 2. В этих случаях 5 и 2 наз. разностью ар. прогрессии.

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "арифметическая":
адъютантская, алевская, амханицкая, англиканская, андриевская, антиклиническая, арестантская, аржановская, артистическая, ассистентская, башкирская, высокая, ганская, люмпенская, маврская, монтерская, окказионалистская, умнёшенькая, хасидская, школярская

Рифмы для этого же слова "арифметическая", но если ударение на последний слог :
аглая, амнистированная.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "арифметическая" :
ревелокая, кугетакая, реьерокая, регачокая, мырыгикая, буьосыкая, рочезокая, кишепикая.



Полные рифмы для слова "прогрессия":
аблепсия, аверсия, автопсия, агалаксия, агерасия, аглоссия, агрессия, адипсия, адмиссия, азельготрипсия, безвкусия, неполногласия, несогласия, поднавесия, полногласия, потассия, равновесия, сия, согласия, фессия

Рифмы для этого же слова "прогрессия", но если ударение на последний слог :
абазия, абакция, абалиенация, абаннация, абартикуляция.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "прогрессия" :
ыонадисия, цыволасия, кагйсасия, ливишосия, пананисия, рохидасия, ролебисия, сораписия.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Арифметическая прогрессия" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-А615, для metaphone-"арифмитичискаaпрaгрисиa" и для double-metaphone ARFM.

См. также

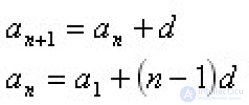... Арифметическая прогрессияОпределение : Свойства : Геометрическая прогрессияОпределение : Свойства ... (СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА)

... , что (постулат Бертрана ). Ряд чисел , обратных к простым , расходится . Более того, при. Любая арифметическая прогрессия вида , где - целые взаимно простые числа , содержит . бесконечно много простых чисел ... ... , содержит . бесконечно много простых чисел (теорема Дирихле о простых числах в.арифметической прогрессии ) Всякое простое число , большее 3 , представимо в виде или , где. - некоторое натуральное число ... (Алгебра)

... , является.выгодное использование неслучайности реальных ключей Например , еслиключи представляют собой арифметическую прогрессию (например , последовательность имен . «Имя 1 »;, «Имя 2 »;, «Имя 3 »;), хеш-функция ... ... 1 »;, «Имя 2 »;, «Имя 3 »;), хеш-функция , использующая умножение , отобразит .арифметическую прогрессию вприближенно арифметическую прогрессию различных хеш-значений , чтоуменьшит количество .коллизий посравнению сослучайной ... (Криптография и криптоанализ, Стеганография и Стегоанализ)

... 1 (для простого скользящего . среднего - SMA ), либо формальные ряды , например , арифметическая прогрессия (WMA ) или.экспоненциальная функция (EMA ) Но в качестве весового коэффициента могут выступать ... ... вес каждого члена исходной функции , начиная с меньшего , равен .соответствующему члену арифметической прогрессии То есть, при вычислении WMA для временного ряда , мы считаем . последние значения исходной ... (Теория вероятностей. Математическая статистика и Стохастический анализ )

... натуральных чисел от 1 до заданного n Если воспользоваться известной формулой для суммы арифметической прогрессии , то вычисления . также потребуют лишь 3 шага : сложение , умножение и деление Если же ... ... o(f(n)) относится к функциям , которые растут быстрее . f(n) Вновь обращаясь к примеру с суммой арифметической прогрессии , можем сказать ., что асимптотическая эффективность алгоритма непосредственного суммирования n элементов соответствует линейной ... (Алгоритмы и теория алгоритмов)

... . Θ( 1 ) Например , Θ( n ) алгоритм является O( n ), а Θ( 1 . ) - нет Упражнение 4 Используя суммирование членов арифметической прогрессии , докажите , что программа выше не . только O( ), но так же и Θ( ). Если вы не знаете , что такое ... ... , что программа выше не . только O( ), но так же и Θ( ). Если вы не знаете , что такое арифметическая прогрессия , то посмотрите . в википедии - это не сложно Поскольку О-сложность алгоритма представляет собой верхний ... (Алгоритмы и теория алгоритмов)

---

---