Аналоговые Усилитель , Сумматор, Дифференциатор, Интегратор на операционных усилителях сущность и применение

Лекция

Сразу хочу сказать, что здесь никакой воды про аналоговый сумматор, и только нужная информация. Для того чтобы лучше понимать что такое аналоговый сумматор, аналоговый дифференциатор, аналоговый интегратор , настоятельно рекомендую прочитать все из категории Электроника, Микроэлектроника , Элементная база.

Схемотехника электронных аналоговых устройств на базе операционных усилителей, конженсаторов и резисторов

Операционные усилители с глубокой отрицательной обратной связью

Для построения различных решающих усилителей применяют операционные усилители с глубокой отрицательной обратной связью.
Основные схемы включения операционных усилителей

Неинвертирующий усилитель;
Инвертирующий усилитель;
Усилитель с дифференциальным входом

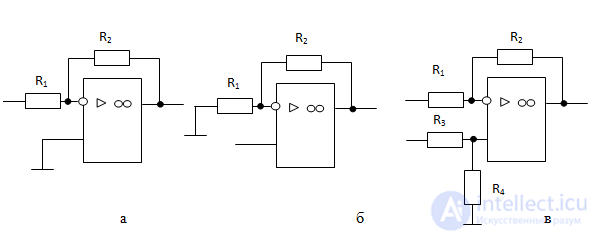
Аналоговые Усилитель , Сумматор, Дифференциатор, Интегратор на операционных усилителях сущность и применение
Рис 1. Схемы включения операционного усилителя: инвертирующее (а); неинвертирующее (б); дифференциальное (в).

Неинвертирующий усилитель
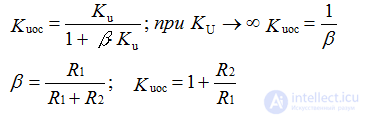
Аналоговые Усилитель , Сумматор, Дифференциатор, Интегратор на операционных усилителях сущность и применение

Инвертирующий усилитель
Kuoc = - R2/R1

При дифференциальном включении ОУ входные напряжения подаются на оба входа через резисторы R1 и R3. При этом равенство потенциалов на входах сохраняется.

Аналоговые Усилитель , Сумматор, Дифференциатор, Интегратор на операционных усилителях сущность и применение

Из этого следует

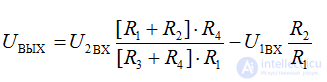
При равенстве R1=R3; R2=R4 следует:

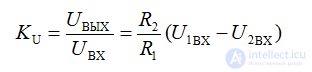
Аналоговые Усилитель , Сумматор, Дифференциатор, Интегратор на операционных усилителях сущность и применение
где в скобках разность напряжений с учетом знака

аналоговый сумматор на операционных усилителях.

На Рис 2 изображена схема усилителя на основе ОУ, выполняющая функцию сумматора.

Аналоговые Усилитель , Сумматор, Дифференциатор, Интегратор на операционных усилителях сущность и применение
Рис 2. Сумматор на основе ОУ с частотно независимыми элементами.

На основании 1-го закона Кирхгофа для узла 1
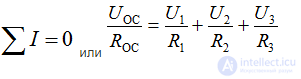
Аналоговые Усилитель , Сумматор, Дифференциатор, Интегратор на операционных усилителях сущность и применение

Т.е., напряжение на выходе усилительной схемы равно напряжениям на входных элементах с весовыми коэффициентами, равными коэффициенту усиления для рассматриваемого входа:

Схема простейшего аналогового сумматора на операционном усилителе приведена на рис. 1. В качестве суммируемых величин выступают входные напряжения U₁ … U_n, в качестве результата — выходное напряжение схемы U_ВЫХ.

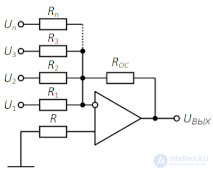
Аналоговые Усилитель , Сумматор, Дифференциатор, Интегратор на операционных усилителях сущность и применение

Рис. 1. Электронный инвертирующий аналоговый сумматор на операционном усилителе.

Аналоговый сумматор — устройство, выполняющее операцию вида:

$Y=k_{1}\cdot X_{1}+k_{2}\cdot X_{2}+...+k_{n}\cdot X_{n},$

где $X_{1},X_{2},...X_{n}$ — некоторые входные аналоговые величины, $k_{1}...k_{n}$ — действительные числа, весовые коэффициенты, $Y$ — выходная аналоговая величина, результат суммирования. Наиболее часто аналоговые сумматоры используются в электронной технике.

Принцип действия

Полагая, что операционный усилитель является идеальным (с бесконечным коэффициентом усиления и нулевыми входными токами), из первого правила Кирхгофа получаем, что ток через резистор R_ОС равен сумме токов через резисторы R₁ … R_n:

$I_{{OC}}=I_{1}+I_{2}+...+I_{n}.$

Так как потенциал инвертирующего входа ОУ в идеальном случае равен 0 из-за действия отрицательной обратной связи (практически весьма близок к 0, т. н. «виртуальная земля»), и, выражая токи через напряжения и сопротивления резисторов, приходим к соотношению:

$-{\frac {U_{{OUT}}}{R_{{OC}}}}={\frac {U_{1}}{R_{1}}}+{\frac {U_{2}}{R_{2}}}+...+{\frac {U_{n}}{R_{n}}}.$

Таким образом, схема рис. 1 выполняет над входными напряжениями операцию суммирования с отрицательными весовыми коэффициентами:

$U_{{OUT}}=-U_{1}{\frac {R_{{OC}}}{R_{1}}}-U_{2}{\frac {R_{{OC}}}{R_{2}}}-...-U_{n}{\frac {R_{{OC}}}{R_{n}}}.$

В случае, если $R_{{OC}}=R_{1}=R_{2}=...=R_{n}$ , схема является инвертирующим сумматором со всеми весовыми коэффициентами равными −1, если же сопротивления резисторов имеют разные значения, получается взвешивающий сумматор, причем весовые коэффициенты для каждой входной переменной равны

$k_{i}=-{\frac {R_{{OC}}}{R_{i}}}.$

Параллельный сумматор

Подключая входные сигналы к инвертирующему и неинвертирующему входам операционного усилителя, можно получить схему, реализующую одновременно сложение и вычитание аналоговых сигналов. Эта схема, называемая параллельным сумматором, изображена на рис. 2. Принцип действия схемы аналогичен принципу действия простейшего сумматора.

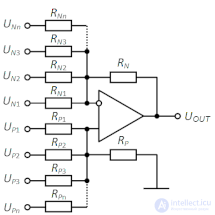
Рис. 2. Электронный аналоговый параллельный сумматор на операционном усилителе.

Полагая, что входные токи операционных усилителей пренебрежимо малы, а потенциалы на его входах равны (U_P = U_N), получим из первого правила Кирхгофа:

$I_{P}=\sum _{{i=1}}^{m}I_{{Pi}};$

$I_{N}=\sum _{{i=1}}^{n}I_{{Ni}};$

${\frac {U_{P}}{R_{P}}}=\sum _{{i=1}}^{m}{\frac {U_{{Pi}}-U_{P}}{R_{{Pi}}}};$

${\frac {U_{P}-U_{{OUT}}}{R_{N}}}=\sum _{{i=1}}^{n}{\frac {U_{{Ni}}-U_{P}}{R_{{Ni}}}}.$

Перенося в левые части двух последних уравнений члены, содержащие U_P, принимая ${\frac {1}{R_{N}}}={\frac {1}{R_{N0}}};{\frac {1}{R_{P}}}={\frac {1}{R_{P0}}}$ получим:

$U_{P}\sum _{{i=0}}^{m}{\frac {1}{R_{{Pi}}}}=\sum _{{i=1}}^{m}{\frac {U_{{Pi}}}{R_{{Pi}}}}.$

$U_{P}\sum _{{i=0}}^{n}{\frac {1}{R_{{Ni}}}}={\frac {U_{{OUT}}}{R_{N}}}+\sum _{{i=1}}^{n}{\frac {U_{{Ni}}}{R_{{Ni}}}}.$

Из обоих уравнений найдем U_P и приравняем правые части полученных выражений:

$U_{P}={\frac {\sum _{{i=1}}^{m}{\frac {U_{{Pi}}}{R_{{Pi}}}}}{\sum _{{i=0}}^{m}{\frac {1}{R_{{Pi}}}}}}={\frac {U_{{OUT}}}{\sum _{{i=0}}^{n}{\frac {R_{N}}{R_{{Ni}}}}}}+{\frac {\sum _{{i=1}}^{n}{\frac {U_{{Ni}}}{R_{{Ni}}}}}{\sum _{{i=0}}^{n}{\frac {1}{R_{{Ni}}}}}}.$

Из последнего выражения находим выходное напряжение схемы:

$U_{OUT}=R_{N}{\frac {{\frac {1}{R_{N}}}+\sum _{i=1}^{n}{\frac {1}{R_{Ni}}}}{{\frac {1}{R_{P}}}+\sum _{i=1}^{m}{\frac {1}{R_{Pi}}}}}\sum _{i=1}^{m}{\frac {U_{Pi}}{R_{Pi}}}-R_{N}\sum _{i=1}^{n}{\frac {U_{Ni}}{R_{Ni}}}.$

Таким образом, схема осуществляет сложение напряжений U_Pi и вычитание напряжений U_Ni с весовыми коэффициентами, равными:

$k_{Pi}={\frac {R_{N}}{R_{Pi}}}{\frac {{\frac {1}{R_{N}}}+\sum _{i=1}^{n}{\frac {1}{R_{Ni}}}}{{\frac {1}{R_{P}}}+\sum _{i=1}^{m}{\frac {1}{R_{Pi}}}}};$

$k_{{Ni}}=-{\frac {R_{N}}{R_{{Ni}}}}.$

Применение сумматоров

Широко используются в вычислительной аналоговой технике, обработке сигналов, телевидении, электроакустике, средствах связи и др. Например, микшер электроакустических сигналов представляет собой сумматор с вручную или автоматически управляемыми весовыми коэффициентами суммирования.

Дифференциатор на операционном усилителе.

Дифференциатор, устройство дифференцирующее — аналоговый функциональный блок в АВМ структурного типа.

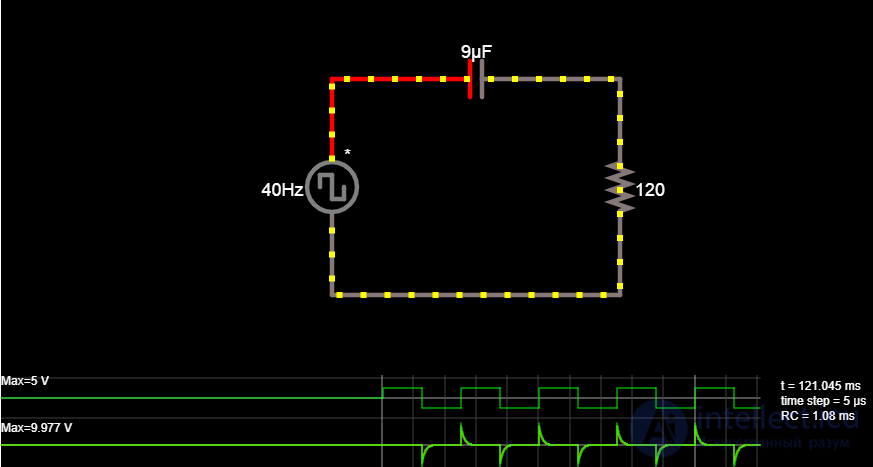
Рис. Пример простейшего дифференциатора на конденсатре

Использование реактивных элементов позволяет реализовать аналоговые операции дифференцирования и интегрирования. Если в схеме входной элемент представляет собой конденсатор емкостью С, а элемент обратной связи – резистор сопротивлением R, то из условия I1=I2 следует, что

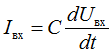откуда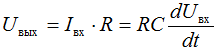

т.е. выходное напряжение является дифференциалом входного напряжения с весовым коэффициентом RC.

Характеристики

Дифференциатор формирует на выходе сигнал, пропорциональный скорости изменения входного воздействия.

Зависимость между входной и выходной величиной можно представить в виде формулы:

$y(t) = -k \frac{dx(t)}{dt}$ ,

где $y(t)$ — выходная величина, $x(t)$ — входная, $k$ — коэффициент передачи.

Напряжение на выходе для идеального дифференциатора вычисляется по формуле:

$u_{\text{out}}(t) = -{R}{C}\frac{du_{\text{in}}(t)}{dt}$ ,

где $u_{\text{out}}$ — выходное напряжение, $u_{\text{in}}$ — входное.

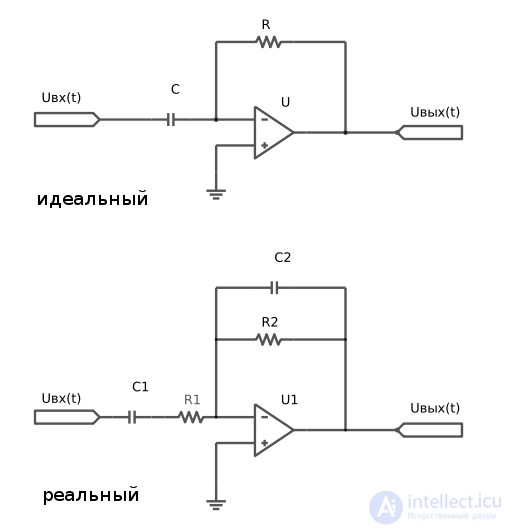
Идеальный дифференциатор способен усиливать паразитные высокочастотные помехи входного сигнала. Об этом говорит сайт https://intellect.icu . На практике применяются схемы дифференциаторов, реализующие операцию дифференцирования приближенно.

Принципиальная схема дифференциатора

Схема идеального дифференциатора представляет собой конденсатор, включенный на вход операционного усилителя, в цепь обратной связи которого включен резистор.

При синусоидальном напряжении дифференциатор ведет себя как фильтр верхних частот, коэффициент усиления которого пропорционален частоте входного сигнала.

Недостаток дифференциатора — чувствительность к шумам высокой частоты. Устраняется это недостаток ограничением усиления на высоких частотах при помощи резистора, включенного последовательно с емкостью. В этом случае схема будет работать как дифференциатор до частот определяемой выражением $F={\frac {1}{2\pi RC}}$ .

Применение аналогового дифференциатора

аналоговый дифференциатор находит широкое применение в электронике и связи, особенно в обработке сигналов, связанных с изменением времени. Он может быть использован для измерения скорости изменения сигнала, а также для выделения высокочастотных составляющих сигнала.

Некоторые примеры применения аналогового дифференциатора:

Обработка аудиосигналов: аналоговый дифференциатор может быть использован для выделения высокочастотных компонентов звукового сигнала, таких как смычковые звуки в музыке.
Измерение скорости: аналоговый дифференциатор может быть использован для измерения скорости изменения сигнала, например, для измерения скорости движения объекта по GPS.
Обработка изображений: аналоговый дифференциатор может быть использован для извлечения границ изображения, что делает его полезным в обработке изображений и компьютерном зрении.
Контроль систем: аналоговый дифференциатор может быть использован для контроля систем, например, для определения скорости изменения температуры в процессе нагрева или охлаждения.
Радиосвязь: аналоговый дифференциатор может быть использован для извлечения высокочастотных сигналов из радиосигнала, что делает его полезным в радиосвязи.

Схема дифференциатора по сути представляет собой фильтр верхних частот . Он может генерировать прямоугольную волну из входной треугольной волны и создавать всплески напряжения в чередующемся направлении, когда применяется прямоугольная волна. В идеальных случаях дифференциатор меняет влияние интегратора на форму волны, и наоборот. Следовательно, они чаще всего используются в схемах формирования сигналов для обнаружения высокочастотных составляющих входного сигнала. Дифференциаторы - важная часть электронных аналоговых компьютеров и аналоговых ПИД-регуляторов . Они также используются в частотных модуляторах в качестве детекторов скорости изменения.

Электронные аналоговые интеграторы на базе резистора и конденсатора

Рис. Электрическая схема простейшего интегратора на пассивных элементах (RC-цепь).

Сейчас это наиболее распространенный тип интеграторов. Мало типов радиотехнических или электронных устройств, где бы не применялись такие интеграторы. Схемотехнически строится на активных и пассивных компонентах. В зависимости от конкретной задачи, обеспечения нужной точности интегрирования, удобства применения, стоимости, строится по схемам различной сложности.

В простейшем случае представляет собой RC-фильтр нижних частот — соединение конденсатора и резистора как показано на рисунке. Дифференциальное уравнение, описывающее эту цепь:

$I=C{\frac {dU_{a}}{dt}}={\frac {U_{e}-U_{a}}{R}}$ ,

где — ток цепи, входной ток, — емкость конденсатора, — сопротивление резистора, $U_{e}$ — входное напряжение интегрирующей цепочки,
$U_{a}$ — выходное напряжение.

Общее решение этого уравнения при произвольном изменении $U_{e}$ :

$U_{a}(t)={\frac {1}{RC}}\int \limits _{-\infty }^{t}{U_{e}({\tau })}e^{-(\tau -t)/RC}\,d{\tau }$ .

Произведение $RC=T$ имеет размерность времени и его называют постоянной времени RC-цепи. Из приведенной формулы очевидно, что простейшая RC-цепь только приближенно выполняет функцию интегрирования из-за экспоненциального сомножителя в подынтегральном выражении. Точность интегрирования повышается при стремлении постоянной времени к бесконечности, что стремит экспоненту к 1. Но при этом выходное напряжение стремится к 0. Таким образом, при повышении точности интегрирования существенно снижается выходное напряжение простейшей интегрирующей цепи, что во многих практических применениях неприемлемо.

Для устранения этого недостатка в схемы интеграторов включают активные электронные компоненты. Простейший интегратор такого типа можно построить на биполярном транзисторе, включенном по схеме с общим эмиттером. В этой схеме значительно повышена точность интегрирования, так как напряжение база-эмиттер при изменении входного тока базы изменяется незначительно и приблизительно равно напряжению на прямосмещенном полупроводниковом p-n переходе. Если входное напряжение база-эмиттер пренебрежимо мало по сравнению с входным напряжением, то точностные свойства такого интегратора приближаются к свойствам идеального интегратора. Нужно отметить, что этот интегратор инвертирующий, то есть при подаче положительного напряжения на вход выходной сигнал будет уменьшаться.

Аналоговые Усилитель , Сумматор, Дифференциатор, Интегратор на операционных усилителях сущность и применение

аналоговый интегратор , построенный на операционном усилителе.

Дальнейшее повышение точности электронных аналоговых интеграторов можно достичь, применяя в качестве активных компонентов операционные усилители (ОУ). Упрощенная схема такого интегратора приведена на рисунке. Идеальный ОУ имеет бесконечный коэффициент усиления и бесконечное входное сопротивление (нулевой входной ток), современные реальные ОУ по этим параметрам приближаются к идеальным — имеют коэффициент усиления более нескольких сотен тысяч и входные токи менее 1 нА и даже пА. Поэтому при упрощенном анализе цепей с ОУ обычно допускают, что ОУ идеальный.

За счет действия отрицательной обратной связи через конденсатор благодаря бесконечному коэффициенту усиления потенциал инвертирующего входа ОУ (обозначен «-») всегда равен нулю, можно считать, что резистор виртуально закорочен на «землю». Благодаря этому ток через резистор не зависит от выходного напряжения интегратора и равен $V_{in}/R$ . Так как этот же ток является током конденсатора (из 1-го правила Кирхгофа, так как ток входа ОУ равен нулю), модуль напряжения на конденсаторе $V_{C}(t)$ выражается:

$V_{C}(t)={\frac {1}{C}}\int \limits _{-\infty }^{t}{I_{C}}(\tau )\,d{\tau }$ .

Подставляя в последнюю формулу выражение для тока резистора имеем:

$V_{out}(t)=-{\frac {1}{RC}}\int \limits _{-\infty }^{t}{V_{in}}(\tau )\,d{\tau }$ .

Знак минус указывает, что ОУ инвертирует сигнал.

Разбивая интервал интегрирования на 2 интервала, первый от $-\infty$ до 0 и второй от 0 до $t$ (в виде суммы 2 интегралов) окончательно имеем:

$V_{out}(t)=V_{0}-{\frac {1}{RC}}\int \limits _{0}^{t}{V_{in}}(\tau )\,d{\tau }$ ,

где $V_{0}$ — начальное выходное напряжение интегратора до начала цикла интегрирования (момент $t = 0$ ).

Неидеальности ОУ и конденсатора влекут ошибки интегрирования. Главная из них — «сползание» выходного сигнала, это выражается в том, что при нулевом входном сигнале выходное напряжение интегратора медленно изменяется. Сползание вызвано, главным образом, ненулевым входным током реальных ОУ, ненулевым входным смещением реальных ОУ, и, в меньшей степени, током утечки заряда конденсатора через его диэлектрик. Иногда параллельно конденсатору умышленно подключают резистор для самосброса со временем интегратора в «ноль». На рисунке утечки конденсатора символически обозначены резистором $R_{f}$ .

Кроме того, входной ток ОУ вызывает паразитное дополнительное падение напряжения на входном резисторе $R_i$ , изменяющее потенциал инвертирующего входа ОУ, что эквивалентно появлению дополнительного входного напряжения смещения ОУ. Для компенсации этого тока включают резистор $R_n$ , если выбрать его сопротивление равным:

$R_{\text{n}}={\frac {1}{{\frac {1}{R_{\text{i}}}}+{\frac {1}{R_{\text{f}}}}}}=R_{\text{i}}||R_{\text{f}}$ ,

то смещение, вызванное входным током полностью компенсируется (в предположении, что входные токи инвертирующего и неинвертирующего входов равны), практически при этом ошибку в смещение потенциала входа ОУ вносит только разность токов входов.

Теми или иными схемными ухищрениями удается практически полностью устранить систематические ошибки электронных интеграторов за счет усложнения схемы. При этом остаются неустраненными случайные ошибки и ошибки, вызванные дрейфом параметров компонентов, например, из-за влияния температуры окружающей среды или старения.

Практические схемы интеграторов, как правило, снабжаются дополнительными электронными ключами для сброса выходного сигнала в ноль и/или задания начального значения.

Интегратор на операционном усилителе.

Интегратор, блок интегрирования — техническое устройство, выходной сигнал (выходная величина, выходной параметр) которого пропорционален интегралу, обычно по времени, от входного сигнала.

В случае, когда к инвертирующему входу подключен резистор, а в цепь обратной отрицательной связи установлен конденсатор, схема с операционным усилителем выполняет функцию интегратора:

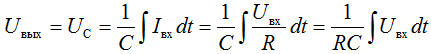
т.е. выходное напряжение является интегралом от входного напряжения.

Пример.
Если на входном резисторе напряжение изменить скачком от 0 до U0, то на выходе ОУ напряжение будет изменяться по закону , т.е. расти пропорционально времени. Это соответствует случаю зарядки конденсатора С постоянным током Iвх=Uвх/R

Повышение точности электронных аналоговых интеграторов можно достичь применяя в качестве активных компонентов операционные усилители (ОУ). Упрощенная схема такого интегратора приведена на рисунке. Идеальный ОУ имеет бесконечный коэффициент усиления и бесконечное входное сопротивление (нулевой входной ток), современные реальные ОУ по этим параметрам приближаются к идеальным — имеют коэффициент усиления более нескольких сотен тысяч и входные токи менее 1 нА и даже пА. Поэтому при упрощенном анализе цепей с ОУ обычно допускают, что ОУ идеальный.

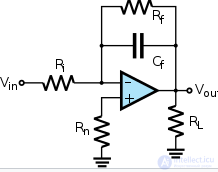
Реальный интегратор на ОУ

$V_{C}(t)={\frac {1}{C}}\int \limits _{-\infty }^{t}{I_{C}}(\tau )\,d{\tau }$ .

Подставляя в последнюю формулу выражение для тока резистора имеем:

$V_{out}(t)=-{\frac {1}{RC}}\int \limits _{-\infty }^{t}{V_{in}}(\tau )\,d{\tau }$ .

Знак минус указывает, что ОУ инвертирует сигнал.

Разбивая интервал интегрирования на 2 интервала, первый от $-\infty$ до 0 и второй от 0 до t (в виде суммы 2 интегралов) окончательно имеем:

$V_{out}(t)=V_{0}-{\frac {1}{RC}}\int \limits _{0}^{t}{V_{in}}(\tau )\,d{\tau }$ ,

где $V_{0}$ — начальное выходное напряжение интегратора до начала цикла интегрирования (момент $t = 0$ ).

$\text{[math]}$ ,

Аналого-цифровые электронные интеграторы

Часто интеграторы строятся по комбинированному принципу. В качестве выходного сигнала у таких интеграторов выступает цифровой код, снимаемый с электронного счетчика или цифрового сумматора. Входной сигнал может быть как чисто аналоговым, так и импульсным или частотным. При аналоговом сигнале его преобразуют в цифровой код с помощью аналого-цифрового преобразователя, далее этот код подается на цифровой сумматор. Другой способ — аналоговый сигнал преобразуют в частоту посредством аналого-частотного преобразователя, выходные импульсы этого преобразователя далее подсчитываются цифровым счетчиком, код которого будет интегралом входного сигнала.

По последней схеме удобно строить интеграторы сигналов датчиков, выходной сигнал которых по своей природе импульсный («события», например, в дозиметрах ионизирующих излучений) или частотный (например, сигналы струнных преобразователей, ЯМР-датчиков магнитометров).

Цифровые интеграторы

В этих интеграторах и входной и выходной сигналы представлены в виде цифровых кодов. По своей сути являются сумматорами с накоплением. На псевдокоде их работу можно описать так:

Выход_интегратора := Выход_интегратора + Вход * Интервал_выборки

Интервал выборки — время от момента получения предыдущего значения до момента получения текущего значения. Не обязательно, чтобы интервал выборки являлся истинным временем. При математическом моделировании реальных процессов (физических, биологических, др.) это может быть масштабированный временной интервал (растянутый или, наоборот, сжатый относительно истинного моделируемого времени) или даже величина невременно́й природы.

Цифровые интеграторы могут быть построены как аппаратно — в виде сумматоров с обратной связью, так и программно.

При аппаратной реализации интегратора по типу сумматора различают:

интегратор с параллельным переносом;
интегратор с последовательным переносом;
интегратор следящий.

Другие типы интеграторов

Аналоговые

В этих приборах входная величина представлена в аналоговом виде, но выходная величина не обязательно аналоговая, даже чаще представлена в цифровом виде, например, в бытовых счетчиках.

Механические вычислительные интеграторы

Исторически первые интеграторы для вычислений представляли собой механические устройства, где величины представлялись в виде углов поворотов и угловых скоростей различных валов, шестерен, фигурных кулачков для вычисления функций. В годы Первой мировой войны широко использовались в приборах управления стрельбой, например, корабельных орудий и приборах управления зенитным огнем.

Со временем в подобные вычислители стали вводить различные электромеханические устройства, электрические автоматические следящие системы. Расцвет таких вычислителей с интеграторами пришелся на годы Второй мировой войны и первые послевоенные годы. Например, вычислители автоматических оптических бомбометательных прицелов бомбардировщиков B-29 (в прицеле ОБП-48 Ту-4) были электромеханическими.

В различные приборы учета расхода и сейчас входят механические интеграторы в виде механических счетчиков — нескольких сцепленных счетных цифровых колец.

Пневматические интеграторы

Принцип действия этих интеграторов основан на вытеснении жидкости из мерного объема, как, например в мерных газовых бюретках, всплывании мерных сосудов или перемещений поршня, снабженного проградуированной шкалой. В этих приборах выполняется интегрирование объемного расхода газа.

Гидравлические интеграторы

По сути объем жидкости в некотором сосуде является интегралом от расхода жидкости в этот сосуд. Если снабдить сосуд шкалой, проградуированной, например, в единицах объема, то получается простейший интегратор расхода жидкости.

Такой интегратор применялся в водяных часах — клепсидре, изобретенных еще в античные времена.

В 1936 году Владимиром Сергеевичем Лукьяновым был создан гидравлический интегратор, предназначенный для решения дифференциальных уравнений.

В 1955 году на Рязанском заводе счетно-аналитических машин начался серийный выпуск интеграторов с заводской маркой «ИГЛ» (интегратор гидравлический системы Лукьянова). Интеграторы получили широкое распространение, посталялись в Чехословакию, Польшу, Болгарию и Китай. С их помощью были проведены расчеты проектов Каракумского канала в 1940-е годы, строительства БАМа в 1970-х. Гидроинтеграторы использовались в геологии, шахтостроении, металлургии, ракетостроении и других областях.

Электрохимические интеграторы

Принцип действия этих интеграторов основаны на законах электролиза Фарадея — количество выделенного или растворенного в процессе электролиза вещества прямо пропорционально электрическому заряду, протекшему в электрохимической ячейке, то есть по сути это количество характеризует интеграл по времени от электрического тока. Такие интеграторы применялись в изобретенных Томасом Эдисоном счетчиках для учета потребленной покупателем электроэнергии. Платеж за электроэнергию рассчитывался по результатам взвешивания электродов гальванической ячейки.

Другие аналоговые интеграторы

Принципиально для создания интегрирующих устройств пригодны любые физические явления, в которых две или более удобно измеримых физических величин (параметров) связаны через интеграл (дифференциал). К таким интеграторам можно, например, отнести интеграторы, основанные на нелинейных электромагнитных свойствах некоторых материалов, — сегнетоэлектриках, ферромагнетиках, дозиметры ионизирующих излучений, основанные на разряде конденсатора через ионизированный излучением газ (индивидуальные дозиметры) и др.

Применение интеграторов

Аналоговый интегратор имеет широкий спектр применения в электронике и связи, особенно в обработке сигналов, связанных с изменением времени. Некоторые примеры применения аналогового интегратора:
Генерация сигналов: аналоговый интегратор может быть использован для генерации сигналов, таких как синусоидальный сигнал, треугольный сигнал или пилообразный сигнал.
Фильтрация сигналов: аналоговый интегратор может быть использован для фильтрации низкочастотных компонентов сигнала.
Измерение времени: аналоговый интегратор может быть использован для измерения времени, например, для измерения времени реакции человека на определенный стимул.
Анализ сигналов: аналоговый интегратор может быть использован для анализа сигналов, например, для измерения площади под кривой сигнала.
Управление системами: аналоговый интегратор может быть использован для управления системами, например, для управления скоростью двигателя или для контроля тока в электрической цепи.
Компенсация ошибок: аналоговый интегратор может быть использован для компенсации ошибок, например, для корректировки входного сигнала, чтобы устранить нежелательные шумы и искажения.
В инерциальных навигационных системах, например, летательных и космических аппаратов, боевых ракет. Двойное интегрирование сигналов датчиков ускорений и датчиков угловых ускорений позволяет вычислить координаты объекта и направления осей объекта не прибегая к внешним наблюдениям.
При учете потребления веществ, сыпучих, жидких и газообразных сред.
Измерении поглощенных и излученных доз излучений разной природы.
Измерении степени заряда и разряда электрохимических источников тока.
Учета наработки, ресурса оборудования.
В технологических процессах, например, при напылении пленок.
Информационной обработке и преобразовании сигналов, электронике, радиотехнике.
В научном экспериментальном оборудовании, измерительных приборах.
В аналоговых вычислительных машинах.

Это не полный список применения аналогового интегратора, но он демонстрирует широкий спектр его применения в электронике и связи.

Вау!! 😲 Ты еще не читал? Это зря!

Счетно-решающий прибор
Микшер
Операционный усилитель
Электронный интегратор
Электронный дифференциатор
Дифференциал ( математика )
Интеграл

Статью про аналоговый сумматор я написал специально для тебя. Если ты хотел бы внести свой вклад в развитие теории и практики, ты можешь написать коммент или статью отправив на мою почту в разделе контакты. Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое аналоговый сумматор, аналоговый дифференциатор, аналоговый интегратор и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Электроника, Микроэлектроника , Элементная база

Очень познавательная статья о применении операционных усилителей для создания аналоговых устройств - сумматоров, дифференциаторов и интеграторов. Интересно узнать о том, как можно использовать такие устройства для аналоговой обработки сигналов.

To reply

Каия

26-03-2023

Я не был знаком с операционными усилителями ранее, поэтому статья стала для меня настоящим открытием. Я понимаю, что такие устройства могут быть полезны в различных областях, таких как автоматика и электроника.

To reply

Расбун

16-02-2023

Я работаю в области электротехники и знаю, как важно правильно подобрать компоненты для создания различных устройств. Статья дает хорошее представление о том, как выбрать операционные усилители для создания аналоговых устройств.

To reply

Толик

16-02-2023

Статья содержит много математических формул и уравнений, но автор хорошо объясняет, как использовать операционные усилители для создания различных устройств. Это очень полезно для тех, кто хочет узнать больше о том, как работают эти устройства.

To reply

Петр

26-03-2023

Я занимаюсь разработкой электронных устройств и мне было очень интересно прочитать о том, как можно использовать операционные усилители для создания сумматоров, дифференциаторов и интеграторов. Я узнал много нового и, надеюсь, смогу применить это знание в своей работе.

To reply

Оставить комментарий

Если у вас есть какое-либо предложение, идея, благодарность или комментарий, не стесняйтесь писать. Мы очень ценим отзывы и рады услышать ваше мнение.

To reply

Comment

Для того, чтобы подтвердить что вы не бот, ответьте:

Name

Email(not published)

Оценить

Аналоговые Усилитель , Сумматор, Дифференциатор, Интегратор на операционных усилителях сущность и применение

Схемотехника электронных аналоговых устройств на базе операционных усилителей, конженсаторов и резисторов

Операционные усилители с глубокой отрицательной обратной связью

аналоговый сумматор на операционных усилителях.

Принцип действия

Параллельный сумматор

Применение сумматоров

Дифференциатор на операционном усилителе.

Характеристики

Принципиальная схема дифференциатора

Применение аналогового дифференциатора

Электронные аналоговые интеграторы на базе резистора и конденсатора

Интегратор на операционном усилителе.

Аналого-цифровые электронные интеграторы

Цифровые интеграторы

Другие типы интеграторов

Аналоговые

Механические вычислительные интеграторы

Пневматические интеграторы

Гидравлические интеграторы

Электрохимические интеграторы

Другие аналоговые интеграторы

Применение интеграторов

Вау!! 😲 Ты еще не читал? Это зря!

Комментарии

Оставить комментарий

Электроника, Микроэлектроника , Элементная база

Термины: Электроника, Микроэлектроника , Элементная база