1.4 Простейший поток вызовов и его свойства кратко

Привет, Вы узнаете о том , что такое простейший поток вызовов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое простейший поток вызовов, его свойства , настоятельно рекомендую прочитать все из категории Теория телетрафика.

Простейшим потоком вызовов называется стационарный ординарный поток без последействия. простейший поток вызовов полностью определяется и задается вероятностью поступления точно К вызовов за время [0,t ) . Обозначим эту вероятность Pk (t) при К=0,1, 2,3,..., и t>0 . Найдем выражение для Pk (t) :

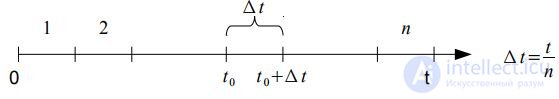
Рассмотрим малую длительность времени Δ t и вычислим вероятность того, что в этот промежуток времени поступит хотя бы один вызов. По определению, параметром потока мы назвали предел отношения:

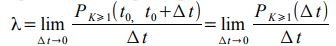
Следовательно, с точностью до бесконечно малых высшего порядка, при Δ t →0 можно считать вероятностью того, что в промежуток времени Δ t поступит хотя бы один вызов, равной:

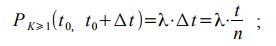
а вероятностью того, что не поступит ни одного вызова, равной:

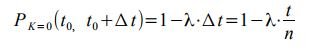
Так как по определени простейший поток — это поток без последействия, то вероятности поступления вызовов в неперекрывающиеся промежутки времени независимы. Об этом говорит сайт https://intellect.icu . Следовательно, n промежутков времени моожно рассматривать как n независимых опытов, в каждом из которых промежуток времени Δ t может быть «занят» с вероятностью λ⋅t /n .

Вероятность того, что среди n промежутков будет ровно К «занятых» можно определить по теореме о повторении опытов (по формуле Бернулли) из выражения 

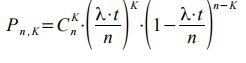
При достаточно большом n эта вероятность приблизительно равна вероятности поступления точно К вызовов в промежуток времени [0,t ) , так как вероятность поступления двух или более вызовов в промежуток Δ t имеет пренебрежимо малую вероятность (простейший поток ординарный!). Чтобы найти точное значение

P k (t) , нужно перейти к пределу при n →∞ : 

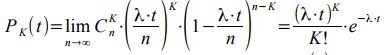
Распределение вероятностей P K (t) называется распределением Пуассона. Чтобы убедиться, что последовательность вероятностей P K (t) представляет собой ряд распределений, необходимо показать, что сумма всех вероятностей P K (t) равна единице. Действительно, исходя из ряда Маклорена

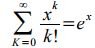
, получим: 

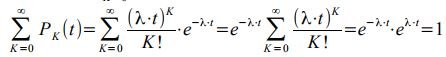
Чтобы построить распределение Пуассона, необходимо для всех К рассчитать P K (t) . Это распределение дискретной случайной величины. При λ⋅t=4 распределение имеет следующий вид: 

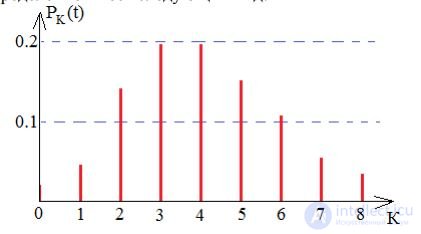
Огибающие распределения Пуассона при различных λ⋅t имеют следующий вид:

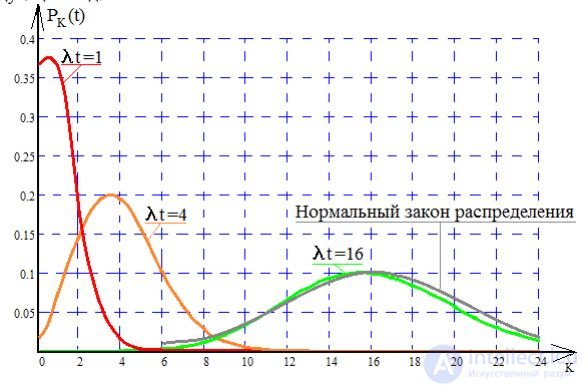
Как видно из рисунка, с возрастанием огибающая принимает все более симметричный вид. При λ⋅t⩾10 имеет место хорошее совпадение между огибающей закона распределения Пуассона и нормальным законом распределения (который является законом распределения непрерывной случайной величины), формула и график которого: 

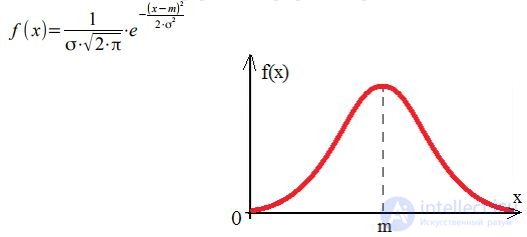
Информация, изложенная в данной статье про простейший поток вызовов , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое простейший поток вызовов, его свойства и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория телетрафика