1.5 Математическое ожидание и дисперсия простейшего потока вызовов кратко

Привет, Вы узнаете о том , что такое ма тическое ожидание, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое ма тическое ожидание, дисперсия простейшего потока вызовов , настоятельно рекомендую прочитать все из категории Теория телетрафика.

Определим математическое ожидание числа вызовов, поступающих за время [0,t ) : 

 

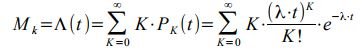
- выражение начального момента первого порядка.

 

Первый член суммы при К=0 равен нулю, следовательно суммирование можно начинать с К=1 :

 

Обозначая K−1=r , с помощью ряда Маклорена получим: 

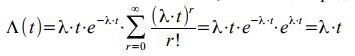
Но с другой стороны: Λ(t)=μ⋅t - по определению для стационарного потока. Следовательно, для простейшего потока интенсивность численно равна параметру - μ=λ Дисперсию случайной величины, распределенной по закону Пуассона, будем определять из выражения:

 

Где M k– математическое ожидание, M k=Λ(t)=λ⋅t , α2 – начальный момент второго порядка.

По определению:

 

 Следовательно:

α2=λ⋅t⋅[λ⋅t+1]

Дисперсия простейшего потока:

Dk=α2−M K 2 =λ⋅t⋅(λ⋅t+1)−(λ⋅t) 2=λ⋅t

Таким образом, дисперсия простейшего потока вызовов равна математическому ожиданию:

M k=Dk=λ⋅t

Из этого свойства простейшего потока следует важный для практики вывод: относительная колеблемость простейшего потока вызовов тем меньше, чем больше его математическое ожидание. Об этом говорит сайт https://intellect.icu . Относительная колеблемость оценивается коэффициентом вариации, отношением: 

 

Рассмотрим два крайних случая: предельное значение, при котором относительная колеблемость равна нулю (соответствует детерминированному потоку) и второй случай при Δ t →0 (относительная колеблемость будет беспредельно увеличиваться).

 

В первом случае, при трех линиях потерь не будет, а η=100% ,

где η= t зан / t набл .

Во втором случае, при трех линиях потерь не будет, но при Δ t →0   η→0 .

η – среднее использование каналов,

t набл — длительность наблюдения,

t зан — длительность занятия одного канала.

Чем выше относительная колеблемость потока вызовов, тем ниже среднее использование каналов в пучке при фиксированном качестве обслуживания ( P=const ). Этим свойством потока объясняется зависимость: 

λ⋅t – математическое ожидание числа вызовов, поступающих за [0,t ) .

 

Отсюда эффективность системы телефонной связи тем выше, чем больше интенсивность поступающего на систему потока вызовов. Это фундаментальное свойство случайных потоков вызовов широко используется в системах массового обслуживания: в телекоммуникациях для концентрации потоков вызовов строят телефонные станции большой емкости и коммутационные узлы; в торговле – супер- и гипермаркеты; на транспорте – крупные аэропорты и вокзалы

 

 

Объединение и разъединение независимых простейших потоков:

Объединение независимых простейших потоков с параметрами λ1 ,λ2 ,λ3 ,... ,λi ,... ,λn тоже будет простейшим потоком с параметром λ=∑  λi , равным сумме параметров объединяемых потоков. 

 

Рекуррентная формула Пуассона:

 

 

Обозначим t в — средняя длительность пребывания в системе одного вызова (обычно принимается t в=1 ). Разделим и умножим t на t в : 

 

 

Учитывая сказанное, для более эффективного обслуживания потоков вызовов желательно производить их объединение.

Без доказательства отметим еще одно интересное свойство простейшего потока: при суммировании большого числа независимы ординарных стационарных потоков с практически любым последействием получается поток, сколь угодно близкий к простейшему.

Аналогия: «при суммировании большого числа независимых случайных величин, подчиненных практически любым законам распределения, получается величина, приближенно распределенная по нормальному закону».

 

Информация, изложенная в данной статье про ма тическое ожидание , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое ма тическое ожидание, дисперсия простейшего потока вызовов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория телетрафика

Из статьи мы узнали кратко, но содержательно про ма тическое ожидание