Лекция
Привет, Вы узнаете о том , что такое система из нейроподобных элементов , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое система из нейроподобных элементов , настоятельно рекомендую прочитать все из категории Нейробионика.
В главе дается формализованное представление об информационных преобразованиях в нервных клетках, их отдельных участках и системах из множества нейронов. Рассмотрены нейроны разных типов. Описана формальная модель «концептуальной рефлекторной дуги», включающей в себя анализирующий и управляющий аппараты. Выходные нейроподобные элементы анализатора дают начало входным каналам управляющей части системы. Особенностью нейроподобных систем является совмещение процесса передачи информации по множеству параллельных каналов с процессом ее одновременной
параллельной переработки. Рассмотрены модели основных механизмов и систем мозга.
Рассмотрены основные типы нейронов, которые, по современным воззрениям, можно выделить в нервной системе. Выделены функционально значимые участки нейронов. Рассмотрены локальные дендритные и нейронные сети.
Из механизмов работы реального нейрона нейробионика выделяет существенные с точки зрения построения эффективных информационных структур. Такой нейрон можно назвать редуцированным, так как он наделен лишь

частью присущих реальному нейрону свойств. В большинстве случаев редуцированный нейрон представляется в виде аналогового элемента — сумматора с коэффициентами входных каналов разного типа: 1 — постоянными коэффициентами, 2 — управляемыми, 3 — перестраивающимися в зависимости от входного по данному каналу сигнала, 4 — коэффициентами типа синапсов Хебба, меняющимися под влиянием выходного сигнала нейрона (рис. 2.1). По мере поступления на входы нейрона сигналов происходит его настройка на некоторый тип входных сигналов.
В нервной системе обнаруживают нейроны, реакция которых на входные сигналы проявляется в градуальном изменении параметров выходного сигнала. Выходной сигнал может быть закодирован частотой генерации импульсов (спайков), длиной пачки импульсов или длительностью временного интервала, отделяющего появление выходного импульса от прихода входного сигнала.
Электрофизиологические и модельные исследования процессов в соме нейрона дают основание выделять две стадии информационного процесса в нейроне:
1) преобразование входных импульсных последовательностей Ft через синаптические контакты st в параметр р (краткое обозначение постсинаптичес-
кого потенциала ПСП или поляризации сомы) и 2) преобразование параметра в последовательность выходных импульсов F нейрона [21, 24]. По экспериментальным данным вторая стадия, преобразования для ряда нейронов [42], имеет значительный участок, близкий к линейному.
Это послужило основанием рассматривать в моделях зависимость F (р) как линейную
F = кр, (1)
где к — коэффициент пропорциональности.
Однако, чтобы подчеркнуть неизбежность насыщения, характеристику F (р) представляют с помощью «ограничивающей
функции» L
F = L{kp}, (2)
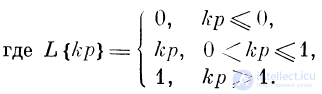
Рассмотрим примеры, характеризующие первую стадию преобразования входных сигналов Ft (1 <= i <=n / где n— число входов) в параметр р\ эта стадия по сути
и определяет функцию нейрона. Нейрон-сумматор. Согласно морфологическим исследованиям существуют нейроны разных типов, отличающиеся количеством синапсов на соме.
Например, мотонейроны [45] и пирамидные нейроны [25] имеют большое количество синапсов на соме. Однако существуют нейроны, практически вообще лишенные дендритов (или имеющих короткие толстые отростки), у которых синаптические контакты располагаются только на соме . Электрофизиологи отмечают способность нейрона к пространственной и временной суммации. Пространственная суммация понимается как свойство суммировать сигналы, приходящие по разным аксонам. Временная суммация подразумевает наличие инерционности, позволяющей складывать воздействия импульсов, приходящих по
одному каналу (аксону). Рассмотрим два примера.
Случай только пространственной суммации, когда по нескольким входам (синапсам) приходит залп одиночных импульсов. Число активированных входов может быть разным: от одного до п. Соответственно будет изменяться и суммарная деполяризация
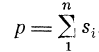
При линейной зависимости F (р) частота следования F выходных импульсов пропорциональна сумме возбужденных входов .
Случай смешанной пространственно-временной суммации, когда по многим (n) входам поступают импульсные последовательности. Каждую последовательность можно характеризовать частотой Fi следования импульсов, и тогда 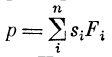 (подробно см. [21]).
(подробно см. [21]).
Нейрон-умножитель. При анализе только временного взаимодействия возбуждений внутри клетки выделяется режим умножения числа входных импульсов на
постоянный коэффициент. Если N и N1 — числа импульсов на входе и выходе клетки, то
N = kN1. (5)
В случае непрерывной импульсации можно говорить о входной F1 и выходной F2 частотах следования импульсов, и тогда 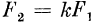
Наблюдаемые электрофизиологами случаи k< 1, к = 1 и к > 1 можно объяснить различием соотношений между постоянными времени нарастания деполяризации,
разрушения медиатора и рефрактерности, т. е. изменения порога после срабатывания [21, с. 23].
В ряде работ [21, 24] обсуждалась возможность перемножения нескольких входных частот F1, F2 и т. д., т. е. выходной сигнал есть F = kF1F2. Однако эта возможность остается гипотетичной.
Предполагается, что нейрон такого типа содержит дендриты, реализующие функции непрерывной логики.
Заметим, что введение порога, нарушающего линейность зависимости F от р, может перевести подобный нейрон-преобразователь в разряд нейронов-детекторов.
Нейрон-преобразователь типа управляемой линии задержки. Предполагается, что нейрон этого типа содержит дендриты, являющиеся управляемой линией задержки, Функция такого нейрона состоит в том, чтобы изменять момент проявления выходного импульса в зависимости от фазовых соотношений в ансамбле импульсов, приходящем по входным волокнам. Можно представить, что задержка в появлении выходного импульса будет минимальной, если ансамбль входных сигналов создает наилучшие условия для проведения некоторого спайка через последовательность дендритных узлов или локальных расширений. Чем больше совокупность входных сигналов отличается от такого ансамбля, тем больше латентность ответа нейрона.
Дискретным фильтром будем называть элемент, способный находиться в двух состояниях — сработал или не сработал, и реагирующий только на сигнал определенного вида.
Элементы совпадения.
Выделение факта одновременного прихода нервных импульсов по двум волокнам является типичной функцией нервных элементов. Ряд физиологических [36, 64], морфологических [6, 98] и модельных [46] исследований дает основания выделить два вида элементов, которые могут быть использованы при решении этой задачи (самостоятельно или в составе нейронной структуры из многих таких элементов). Элемент первого вида срабатывает, если различие моментов прихода входных импульсов к соме не превышает 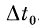 . Можно предложить три способа реализации такого элемента в нервной системе: входные сигналы могут приходить к соме по дендритам, дендритам и соматическим синапсам или только по соматическим синапсам.
. Можно предложить три способа реализации такого элемента в нервной системе: входные сигналы могут приходить к соме по дендритам, дендритам и соматическим синапсам или только по соматическим синапсам.
Элемент второго вида выполняет функцию, «дополнительную» к функции элемента первого вида: срабатывает, если различие между моментами прихода входных импульсов к соме клетки  и не срабатывает, если меньше
и не срабатывает, если меньше 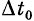
Нетрудно представить возможность образования сложных, или «комплексных», нейронов в виде различных комбинаций из элементов разных типов. Например, нейрон —
детектор ансамбля сигналов, в котором кодовые посылки приходят по многим волокнам. Такой элемент содержит составные части, фиксирующие появление каждой отдельной кодовой посылки, а в целом он выделяет определенный ансамбль таких посылок. Этот случай является усложнением элемента второго типа. Возможно существование нейрона-преобразователя, который объединял бы как функции дискретного фильтра, так и функции преобразователя аналоговых величин; например, такой элемент мог бы действовать по принципу реализации условных операций или быть просто пороговым сумматором. Относительно реализации сложного фильтра (или преобразователя) могут быть сомнения: выполняет ли соответствующие функции сложный нейрон с разветвленными
дендритами или соединение нейронов. По мере расширения представлений об операциях в дендритах потенциальные возможности нейрона видятся все более сложными. При этом сложность нейрона предстает не только зависящей от возможности реализовать ту или иную функцию, но также и от целесообразности объединения многих операций в одном элементе, а это уже определяется требованиями структуры, в которую входит элемент. Рассмотрение всевозможных комбинаций элементарных дендритных звеньев, которые могут определить функцию нейрона в целом, не входит в задачу работы. Поэтому здесь обсуждены лишь несколько примеров элементов, относительно которых можно предполагать, что они воплощены в виде нейрона. Упор сделан на попытки привести доводы физиологического характера, которые могли бы укрепить предсаавления о возможности существования подобных нейронов.
Можно указать еще один вероятный тип нейрона — дискретного фильтра: детектор ансамблей сигналов, каждый из которых состоит из последовательности импульсов, характеризующейся аналоговым параметром — частотой следования импульсов. Предполагается, что сигналы существуют в течение времени, достаточного дляопределения частоты. В этом случае ансамбли различаются набором аналоговых величин.
Важной структурой, являющейся результатом объединения редуцированных нейронов, является концептуальнал рефлекторная дуга, ставящая в соответствие
определенным сигналам определенные реакции.
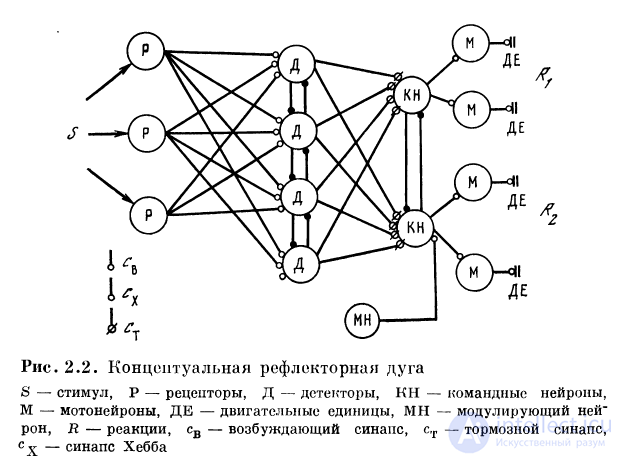
В основе нейронной организации концептуальной рефлекторной дуги лежит принцип кодирования номером канала, заключающийся в том, что определенным параметром сигнала на входе и определенным реакциям на выходе системы ставятся в соответствие специализированные нейроны. Кодирование сигнала номером канала означает, что при определенном входном сигнале на одном из специализированных нейронов достигается максимум возбуждения. При изменении сигнала этот максимум перемещается на другой специализированный нейрон. Вследствие определенной организации связей образуются специализированные нейроны, селективно настроенные на разные сигналы. Такие нейроны называются нейронами-детекторами или просто детекторами. Нейроны-детекторы образуют целые наборы или поверхности, на которых отображаются внешние сигналы (рис. 2.2).
Простейшей детекторной системой является набор детекторов, представляющих рецепторы кожной поверхности. Перемещение сигнала по кожной поверхности кодируется перемещением максимума возбуждения по множеству детекторов локальных положений стимула. Принцип отображения на множество детекторов был затем использован и для сигналов, которые не могут непосредственно перемещаться по рецепторной поверхности. Так, анализ направления силы тяжести достигается формированием пространственно-поляризованных рецепторов.
Множество по-разному ориентированных волосков волосковых клеток органа равновесия — статоциста
—образует рецептивную поверхность, по которой перемещается
фокус возбуждения, когда животное передвигается в поле
тяжести. Центральные нейроны-детекторы образуют
поверхность, на которой отражается положение животного
в поле силы тяжести.
Более сложный случай отображения сигнала на
множество детекторов возникает тогда, когда рецепторы на
входе обладают широкополосными харак!ерис1иками,
перекрывающимися относительно детектируемого
параметра сигнала. В этом случае множество селективных
детекторов образуется в результате поляризации связей между
рецепторами и детекторами, обеспечивающих
определенную степень возбуждения того или иного детектора. Так,
при определенной длине волны света меняется
комбинация возбуждения трех типов колбочек. За счет разных
коэффициентов связи рецепторов с детекторами
максимум возбуждения возникает в селективном
нейроне-детекторе цвета. Изменение длины волны света ведет к
изменению комбинации возбуждений рецепторов и
перемещению максимума возбуждения на другой детектор.
Таким образом, общий принцип кодирования номером
канала заключается в том, что множество внешних
сигналов отображается на множество селективных детекторов,
образующих в мозгу аналог рецептивной поверхности —
квазирецептивную поверхность.
Принцип кодирования номером канала
распространяется и на реакции. В этом случае единичное возбуждение
нейрона через дерево связей с другими нейронами
превращается в сложный аккорд движения — специфическую-
реакцию. Нейроны, при возбуждении которых
запускается целая реакция или ее фрагмент, называют командными.
Таким образом, набору командных нейронов
соответствует набор реакций. При перемещении возбуждения по
множеству командных нейронов возникает последовательность
аккордов движений — последовательность
фиксированных программ движений.
Селективное возбуждение соответствующего
командного нейрона через мотонейроны и мышечные единицы управляет реакцией. Совокупность подключенных к
командному нейрону детекторов образует рецептивное поле этого
командного нейрона. Детекторы, эффективные в
отношении возбуждения командного нейрона, образуют его
эффективное рецептивное поле, совпадающее с рецептивным
полем реакции, которую данный командный нейрон
включает. Связи детекторов с командными нейронами могут
быть стабильными и пластичными. В случае стабильных
связей реакция возникает по принципу «ключ — замок»:
ключом является внешний стимул, а замок — набор
связей детекторов с командным нейроном, необходимым для
запуска реакции.
Пластичные связи детекторов с командными
нейронами зависят от реализуемой связи (синапсы Хебба) или
перестраиваются под влиянием сигналов. В ходе
обучения пластичные связи детекторов с командными
нейронами обеспечивают подключение одних детекторов и
отключение других от командного нейрона, что эквивалентно
изменению структуры эффективного рецептивного поля
реакции. В зависимости от состояния возбужденной среды
организма значение разных реакций в разные моменты
времени меняется. Иными словами, меняются приоритеты
реакций, задаваемые специальными нейронами,
оценивающими состояние внутренней среды организма. Такие
нейроны не вызывают реакций командных нейронов, а
только изменяют их возбудимость. Эти нейроны называются
модулирующими.
Совокупность рецепторов, детекторов, командных
нейронов, мотонейронов и эффекторов вместе с
модулирующими нейронами образует концептуальную
рефлекторную дугу (рис. 2.2). Система детекторов также построена
по иерархическому принципу. Между рецепторами и
селективными детекторами расположен промежуточный
слой детекторов, согласующий их характеристики.
Промежуточные детекторы можно назвать первичными, а
селективные детекторы квазирецеитивной поверхности —
вторичными.
Иерархической может быть и система командных
нейронов. Ближайшие к моюнейронам командные нейроны
назовем вторичными, а командные нейроны верхнего
уровня — первичными. Универсальным механизмом обостроения селективности возбуждения является механизм
латерального торможения, благодаря которому
максимально возбужденный детектор оказывает тормозное воздействие на соседние с ним детекторы. Аналогичный
механизм действует и между командными нейронами,
представляющими разные реакции. Принятие решения —
выбор реакции — осуществляется формированием
максимума возбуждения на одном из командных нейронов
вследствие определенных коэффициентов связей его с
детекторами и вкладов модулирующих нейронов.
Прохождение сигнала в концептуальной рефлекторной
дуге вызывает комбинацию возбуждений рецепторов,
которая, проходя через связи с разными коэффициентами
передачи, преобразуется в возбуждение первичных
детекторов. Комбинация возбуждений первичных детекторов
поступает через систему связей с разными
коэффициентами к вторичным детекторам, формируя на одном из них
максимум возбуждения. В результате латерального
торможения селективность вторичных детекторов повышается.
Все детекторы потенциально связаны со всеми
командными нейронами, но в процессе обучения связи меняются:
одни связи усиливаются, другие ослабевают. В
результате каждый командный нейрон возбуждается только
определенными детекторами. Приоритет реакции зависит от
условий внутренней среды организма, которая через
посредство модулирующих нейронов влияет на командные
нейроны. Выбор реакции достигается образованием
максимума возбуждения на одном из командных нейронов.
За счет механизмов латерального торможения
подавляются конкурирующие реакции на других командных
нейронах. Возбужденный командный нейрон через систему
связей с мотонейронами и моторными единицами реализует
специфическую реакцию.
Прохождение сигналов в концептуальной
рефлекторной дуге удобно описывать матрицами возбуждений и
коэффициентов связей, благодаря чему достигается
сжатое представление о реакциях в разных точках
концептуальной рефлекторной дуги сразу для целого ряда
сигналов. При функционировании концептуальной
рефлекторной дуги каждый сигнал должен
рассматриваться независимо от другого, но матричное
описание позволяет дать общее представление о
целой серии опытов, в каждом из которых действует один
сигнал, позволяет рассчитать коэффициенты связей,
а затем по известным коэффициентам связей и матрице
возбуждения рассчитать неизвестное возбуждение.
1 стадия. Сигнал Si порождает в рецепторах век- тор возбуждения рг-, компонентами которого являются возбуждения ptj отдельных рецепторов. В результате
воздействия набора стимулов получается набор векторов возбуждения р,, образующих матрицу || ptj \\ возбуждений
рецепторов по набору сигналов, где i = 1, 2, . . ., т — индекс сигнала; / = 1, 2, . . ., п — индекс рецептора.
II стадия. Преобразование в звене рецептор— первичный детектор. При действии стимула St возникающий в рецепторах вектор возбуждения рг- через связи Bjk с первичными детекторами создает новый вектор возбуждения it в первичных детекторах. При действии серии стимулов эти векторы образуют матрицу возбуждений || fik ||, где А=1, 2, . . ., р — индекс первичного детектора. Через систему связей Bik вектор возбуждения рецепторов р;, созданный стимулом, генерирует вектор возбуждения it первичных детекторов. Обобщая по всем стимулам, получаем матрицу возбуждений первичных детекторов: \\fik || = \\ри || || Bjk\\.
III стадия. Преобразование сигналов St в звене
первичные детекторы — вторичные селективные детекторы.
Через систему связей || ск1 || первичных детекторов
с вторичными детекторами вектор возбуждения первичных
детекторов р*, порожденный сигналом на входе St,
генерирует вектор возбуждения йц вторичных детекторов.
Обобщая по всем стимулам St, получаем матрицу
возбуждений вторичных детекторов: || dtl \\ = \\ fik || || сы ||, где
i = 1, 2, . . ., т — индекс стимула; I = 1, 2. , . ., р —
индекс вторичного детектора.
Наличие латеральных связей приводит к
преобразованию исходной матрицы || dit || возбуждений вторичных
детекторов в итоговую матрицу возбуждений || d*it ||.
IV с т а д и я. Преобразование в звене, вторичные
детекторы — командные нейроны. Основное значение имеет
в этом преобразовании обучающаяся матрица || qu ||
связей селективных нейронов-детекторов с командными
нейронами, перестраивающаяся в процессе обучения в
соответствии с принципом синапсов Хебба, переходя в
матрицу обученного состояния || д* ||.
Возбуждение командных нейронов определяется
матрицей || kit || = || dn || || qlt ||, где I = 1, 2, . . ., и — индекс
вторичного детектора; £=1,2.,.., г; —индекс
командного нейрона; i = 1, 2, . . ., т — индекс стимула.
V с т а д и я. Принятие решения, которое сводится к
выбору максимально возбужденного нейрона с учетом
латерального торможения между командными нейронами.
|| Щ || — матрица возбуждений командных нейронов,
преобразованная латеральным торможением; || kit || —
матрица возбуждений командных нейронов после учета
функций модулирующих нейронов; || Ъ*ц || — окончательная
матрица возбуждений командных нейронов после
операций модуляции и латерального торможения.
В звене принятия решения происходит переход от
количественной меры возбуждения командных нейронов к
реакции «все или ничего». В каждый данный момент
реализуется возбуждение только одного командного нейрона.
Поскольку в каждый данный момент времени вклад
модулирующих нейронов и фактор обучения различны, то и
возбуждение командного нейрона является случайной
величиной \it, где i -— 1, 2, . . ., т — индекс стимула, t =
= 1, 2, . . ., х —индекс командного нейрона, || \ц || —
матрица случайных величин — тех возбуждений, которые
возникают при действии стимулов.
Таким образом, при действии каждого стимула St
выбор максимального возбуждения осуществляется из
ряда случайных величин. Следовательно, переход от стимула
St к реакции R^ (St —>■ /?ю) характеризуется вероятностью
перехода. По всем стимулам имеем матрицу переходов
или матрицу смешения стимул-реакции || ri(d ||, где
i = l, 2, ..., wi — индекс стимула; <о = 1, 2, . . ., z —
индекс реакции; ци — случайные влияния на командный
нейрон Si -> #(о при maxr || lit ||, lit = kit + v\lt.
Если исключить все случайные влияния, а стимулы
выбрать различными, то вероятность перехода Si —> R^
будет иметь значение 0 или 1. Тогда каждый стимул в
наборе стимулов можно характеризовать вектором
вероятностей реакций с компонентами, принимающими значения
О и 1. Наличие случайных влияний в звене командных
приводит к тому, что один и тот же сигнал может
вызывать разные реакции с различной вероятностью.
VI стадия. Выработка управляющего вектора
посредством связей командного нейрона с мотоиейронами.
Коэффициенты связей каждого командного нейрона с
мотонейронами различны. При возбуждении командного
нейрона возникает специфическая комбинация
возбуждений мотонейронов, которая определяет поведенческую
реакцию. Обобщая данные по всем стимулам в случае, когда
стимул однозначно связан с определенным командным нейроном, получаем матрицу || vi8 || возбуждений
мотонейронов в виде || vis || = || kft || || uts ||, где i = 1, 2, . . .
..., т — индекс стимула; s = 1, 2,. . ., ж — индекс
мотонейрона; || Ujs || — матрица связей командных нейронов с
мотонейронами; £ = 1,2,. . ., у — индекс командного
нейрона; || кц || — матрица возбуждений командных нейронов.
VII стадия. Генерация специфической
поведенческой реакции. Определенная комбинация возбуждения мотонейронов приводит к специфической поведенческой
реакции. При прохождении сигналов в концептуальной
рефлекторной дуге решаются следующие задачи.
1. Определение матрицы возбуждений первичных
детекторов || fik || по известным матрице связей рецепторов
с первичными детекторами || bik || и матрице возбуждений
рецепторов || ри ||:
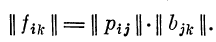
2. Определение матрицы связей || bjk || по известным
матрице возбуждений рецепторов || ptj || и матрице
возбуждений первичных детекторов || fik ||:
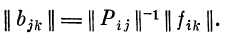
Решение возможно, если матрица || pij || имеет обратную
матрицу. Для существования обратной матрицы
необходимо, чтобы исходная матрица была квадратной: число
стимулов i должно быть равно числу рецепторов /.
Правильность решения может быть проверена при помощи
восстановления матрицы || fik || но рассчитанной матрице
|| bjk || и матрице Ц/?!/!!:
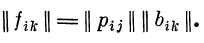
3. Найти матрицу возбуждений на входе по матрице
связей и матрице возбуждений на выходе. Задача не
имеет однозначного решения, поскольку число
неизвестных в ] раз больше числа уравнений. Для нахождения
матрицы возбуждений на выходе требукпся
дополнительные ограничения или условия.
2.1.6. Селективный (вторичный) детектор Dj
Детектор D7- представляет собой редуцированный нейрон аналогового типа, производящий суммирование попарных произведений возбуждений и коэффициентов синаптическои связи ci:
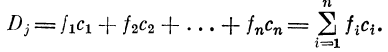
Отдельные возбуждения /г- поступают по аксонам от
первичных детекторов.
Все множество возбуждений, поступающих от
первичных детекторов по независимым каналам, образует
вектор возбуждения F = (/ь /2, . . ., /п), компонентами
которого являются возбуждения в отдельных каналах ft.
Множество независимых синаптических контактов
образует вектор связей с =■ (с2, с2, . . ., с). Вклад данного
канала в реакцию нейрона определяется произведением
возбуждения на коэффициент связи. Эти произведения
суммируются по всем входам. Итоговый эффект на нейроне-
детекторе — скалярное произведение вектора
возбуждений на вектор связей:
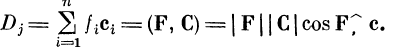
В случае коллинеарности векторов косинус угла между
ними равен единице и скалярное произведение достигает
максимума.
Селективность детектора обусловлена специфичностью
набора коэффициентов синаптических связей, чю делает
нейрон селективно настроенным на определенную
комбинацию возбуждений первичных детекторов, а
следовательно, и на тот сигнал, который эту комбинацию
возбуждений порождает.
Отсюда следует важный вывод: сигналы, вызывающие
одинаковые комбинации возбуждений и создающие
максимум возбуждения на одном и том же детекторе, не
различаются системой, даже если их физические
характеристики существенно различны. Коэффициешы связей
каждого селективного детектора с первичными
детекторами постоянны. Внешний сигнал порождает разные
комбинации возбуждений первичных детекторов — разные
векторы возбуждений.
Рассмотрим вопрос, когда селективный детектор
отвечает максимальным возбуждением. Этот вопрос имеет
смысл лишь в том случае, когда векторы возбуждения
имеют постоянный модуль. Что касается вектора связей,
то он является стабильной характеристикой данного
селективного детектора. При изменении сигналов и соот-
ветственно векторов связей ответ нейрона будет меняться
и достигнет максимума тогда, когда вектор возбуждения
будет коллинеарен вектору связей. В этом случае
компоненты вектора связи и вектора возбуждений
пропорциональны. Выражая компоненты вектора возбуждений через
компоненты вектора связей, приходим к выводу, что
компоненты селективного детектора удовлетворяют
уравнению сферы, если его возбуждение максимально:
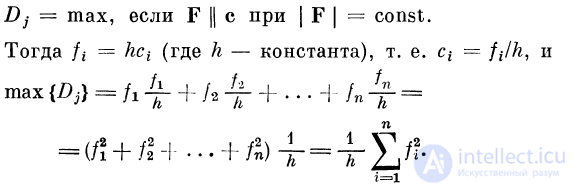
2.1.7. Избирательная характеристика детектора
Каждый детектор характеризуется определенным набором
коэффициентов связей. При изменении входного сигнала
на детекторы поступают изменяющиеся композиции
возбуждений. Каждый детектор будет выделять ту из них,
которая соответствует его вектору связей. Таким образом,
детектор обладает избирательной характеристикой,
выделяя тот сигнал, который порождает на его входах
определенные соотношения возбуждений. Простейшим будет
детектор с двумя входами, каждый из которых
определяется значением коэффициента связи. В зависимости от этих
коэффициентов связи детектор будет настроен на
определенный входной сигнал, а именно тот, который создает
на его входах возбуждения, пропорциональные
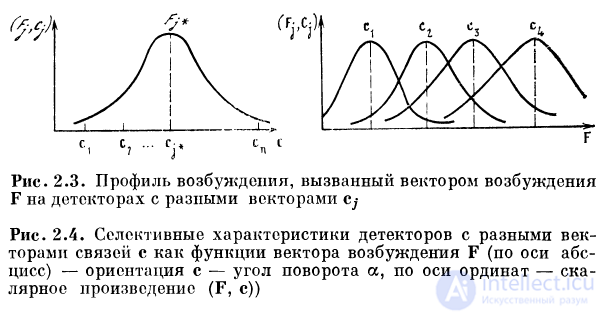
коэффициентам связей. Об этом говорит сайт https://intellect.icu . На рис. 2.3 представлен профиль
возбуждения, вызванный вектором возбуждения F на детекторах
с разными векторами с. Здесь по оси абсцисс отложен
угол ориентации вектора Cj, но оси ординат —
скалярное произведение g = (F, с). Отдельный детектор будет
обладать избирательной характеристикой, которую
можно рассчитать, положив фиксированными компоненты
вектора связи с и изменяя соотношение компонентов вектора
возбуждения F. Если значения компонентов F для
каждого значения сигнала на входе известны, то избирательная
характеристика g детектора может быть представлена в
виде скалярного произведения с на F : g = (cF). Это
произведение достигает максимума тогда, когда F коллинеарен вектору с. При этом компоненты F пропорциональны
компонентам с. Тогда одни компоненты можно выразить
через другие. Отсюда следует, что сумма квадратов
компонентов F при достижении максимума есть некоторая
константа. Если принять, что другие детекторы также
отвечают максимумом реакции при другом значении F
и что коэффициенты пропорциональности для данной
популяции детекторов одинаковые, то максимумы ответов
детекторов удовлетворяют уравнению сферы.
Следовательно, каждый детектор, реакция которого достигает
максимума при определенном значении компонентов, можно
представить точкой на поверхности тг-мерной сферы, ее
размерность определяется числом независимых входов
детектора.
2.1.8. Набор селективных детекторов (рис. 2. 4)
Все детекторы набора обладают векторами связей с*, их
модуль \ct\ = c0. Изменение общего внешнего сигнала
приводит к изменению компонентов F. Максимум
возбуждения g перемещается по набору детекторов,
отображая изменение сигнала. Латеральное торможение между
детекторами выполняет функцию нормирования
возбуждения. Вследствие этого признаки сигнала выделяются
детекторами независимо от интенсивности сигнала.
Каждому значению определенного свойства сигнала
соответствует свой максимум на одном из детекторов набора.
Таким
продолжение следует...
Часть 1 2 ОБЩАЯ ТЕОРИЯ ОРГАНИЗАЦИИ СИСТЕМ ИЗ НЕЙРОПОДОБНЫХ ЭЛЕМЕНТОВ
Часть 2 2.1.16. Описание анализатора матричными уравнениями - 2 ОБЩАЯ ТЕОРИЯ ОРГАНИЗАЦИИ
Часть 3 2.1.21. возрастание различительной чувствительности под влиянием адаптации первичных детекторов -
Часть 4 - 2 ОБЩАЯ ТЕОРИЯ ОРГАНИЗАЦИИ СИСТЕМ ИЗ НЕЙРОПОДОБНЫХ ЭЛЕМЕНТОВ
Комментарии
Оставить комментарий
Нейробионика
Термины: Нейробионика