Лекция
Привет, Вы узнаете о том , что такое квантовый компьютер , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое квантовый компьютер , квантовые алгоритмы, квантовое превосходство , настоятельно рекомендую прочитать все из категории Квантовая информатика.
квантовый компьютер — вычислительное устройство, которое использует явления квантовой суперпозиции и квантовой запутанности для передачи и обработки данных. Хотя появление транзисторов, классических компьютеров и множества других электронных устройств связано с развитием квантовой механики и физики конденсированного состояния, информация между элементами таких систем обычно передается в виде электрического напряжения.
Полноценный квантовый компьютер является пока гипотетическим устройством, сама возможность построения которого связана с серьезным развитием квантовой теории в области многих частиц и сложных экспериментов; эта работа лежит на переднем крае современной физики.
Первым практическим высокоуровневым языком программирования для такого вида компьютеров считается язык Quipper, основанный на Haskell .
Квантовый компьютер — устройство, которое выполняет вычисления, основываясь на законах квантовой механики.
Классический компьютер хранит в памяти L бит, которые за каждый такт работы процессора подвергаются изменению.
В квантовом компьютере в памяти (регистр состояния) хранятся значения L кубитов, однако квантовая система находится в состоянии, являющемся суперпозицией всех базовых 2L состояний, и изменение квантового состояния системы, производимое квантовым процессором, касается всех 2L базовых состояний одновременно.
Соответственно в квантовом компьютере вычислительная мощность достигается за счет реализации параллельных вычислений, причем теоретически квантовый компьютер может работать в экспоненциальное число раз быстрее, чем классическая схема.
Основным элементом квантового компьютера являются квантовые биты, или кубиты (quantum bit, qubit).
Кубит допускает два собственных состояния, обозначаемые |0> и |1>, но при этом может находиться и в их суперпозиции, то есть в состоянии А*|0>+В*|1>, где A и B - любые комплексные числа, удовлетворяющие условию | A |2 + | B |2 = 1.
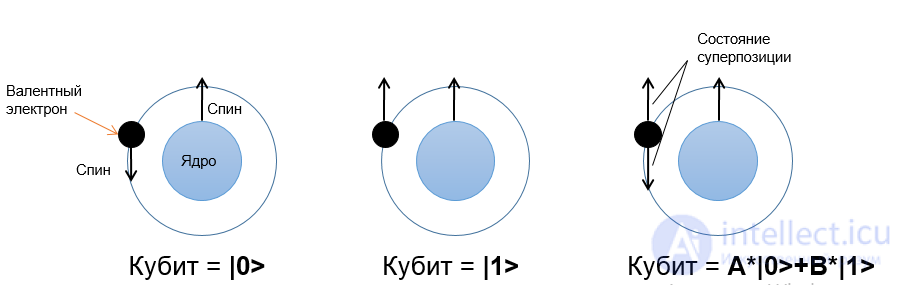
Свойство квантовых частиц быть одновременно во многих состояниях называется квантовым параллелизмом

Квантовый компьютер, благодаря своим качествам, способен разложить 250-значное число на множители не за 800 тысяч лет, как современные самые мощные ЭВМ, а за 30 минут(!). С такой машиной спецслужбы могут быстро взломать любой, самый сложный шифр.
В настоящее время в исследования квантовой криптографии вкладываются большие средства, и значительная часть исследований осуществляется на средства оборонных ведомств и спецслужб.
Идея о квантовых вычислениях была высказана Юрием Маниным в 1980 году .
Одна из первых моделей квантового компьютера была предложена Ричардом Фейнманом в 1981 году. Вскоре Пол Бениофф описал теоретические основы построения такого компьютера .
Так же концепцию квантового компьютера в 1983 предлагал Стивен Визнер в статье, которую он пытался опубликовать в течение более десяти лет до этого.
Необходимость в квантовом компьютере возникает тогда, когда мы пытаемся исследовать методами физики сложные многочастичные системы, подобные биологическим. Пространство квантовых состояний таких систем растет как экспонента от числа 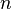 составляющих их реальных частиц, что делает невозможным моделирование их поведения на классических компьютерах уже для
составляющих их реальных частиц, что делает невозможным моделирование их поведения на классических компьютерах уже для  . Поэтому Визнер и Фейнман высказали идею построения квантового компьютера.
. Поэтому Визнер и Фейнман высказали идею построения квантового компьютера.
Квантовый компьютер использует для вычисления не обычные (классические) алгоритмы, а процессы квантовой природы, так называемые квантовые алгоритмы , использующие квантовомеханические эффекты, — такие как квантовый параллелизм и квантовая запутанность.
Если классический процессор в каждый момент может находиться ровно в одном из состояний  (обозначения Дирака), то квантовый процессор в каждый момент находится одновременно во всех этих базисных состояниях, при этом в каждом состоянии
(обозначения Дирака), то квантовый процессор в каждый момент находится одновременно во всех этих базисных состояниях, при этом в каждом состоянии  — со своей комплексной амплитудой
— со своей комплексной амплитудой 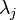 . Это квантовое состояние называется «квантовой суперпозицией» данных классических состояний и обозначается как
. Это квантовое состояние называется «квантовой суперпозицией» данных классических состояний и обозначается как

Базисные состояния могут иметь и более сложный вид. Тогда квантовую суперпозицию можно проиллюстрировать, например, так: «Вообразите атом, который мог бы подвергнуться радиоактивному распаду в определенный промежуток времени. Или не подвергнуться. Мы можем ожидать, что у этого атома есть только два возможных состояния: „распад“ и „не распад“, <…> но в квантовой механике у атома может быть некое объединенное состояние — „распада — не распада“, то есть ни то, ни другое, а как бы между. Вот это состояние и называется „суперпозицией“» .
Квантовое состояние  может изменяться во времени двумя принципиально различными путями:
может изменяться во времени двумя принципиально различными путями:
Если классические состояния  есть пространственные положения группы электронов в квантовых точках, управляемых внешним полем
есть пространственные положения группы электронов в квантовых точках, управляемых внешним полем 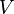 , то унитарная операция есть решение уравнения Шредингера для этого потенциала.
, то унитарная операция есть решение уравнения Шредингера для этого потенциала.
Измерение есть случайная величина, принимающая значения 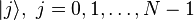 с вероятностями
с вероятностями 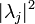 соответственно. В этом состоит квантовомеханическое правило Борна. Измерение есть единственная возможность получения информации о квантовом состоянии, так как значения
соответственно. В этом состоит квантовомеханическое правило Борна. Измерение есть единственная возможность получения информации о квантовом состоянии, так как значения 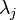 нам непосредственно недоступны. Измерение квантового состояния не может быть сведено к унитарной шредингеровской эволюции, так как, в отличие от последней, оно необратимо. При измерении происходит так называемый коллапс волновой функции
нам непосредственно недоступны. Измерение квантового состояния не может быть сведено к унитарной шредингеровской эволюции, так как, в отличие от последней, оно необратимо. При измерении происходит так называемый коллапс волновой функции  , физическая природа которого до конца не ясна. Спонтанные вредоносные измерения состояния в ходе вычисления ведут к декогерентности, то есть отклонению от унитарной эволюции, что является главным препятствием при построении квантового компьютера (см. физические реализации квантовых компьютеров).
, физическая природа которого до конца не ясна. Спонтанные вредоносные измерения состояния в ходе вычисления ведут к декогерентности, то есть отклонению от унитарной эволюции, что является главным препятствием при построении квантового компьютера (см. физические реализации квантовых компьютеров).
Квантовое вычисление есть контролируемая классическим управляющим компьютером последовательность унитарных операций простого вида (над одним, двумя или тремя кубитами). В конце вычисления состояние квантового процессора измеряется, что и дает искомый результат вычисления.
Содержание понятия «квантовый параллелизм» в вычислении может быть раскрыто так: «Данные в процессе вычислений представляют собой квантовую информацию, которая по окончании процесса преобразуется в классическую путем измерения конечного состояния квантового регистра. Выигрыш в квантовых алгоритмах достигается за счет того, что при применении одной квантовой операции большое число коэффициентов суперпозиции квантовых состояний, которые в виртуальной форме содержат классическую информацию, преобразуется одновременно» .
Прототипы квантовых компьютеров существуют уже сегодня. Правда, пока что экспериментально удается собирать лишь небольшие регистры, состоящие всего из нескольких квантовых битов. К сожалению, существующие квантовые системы еще не способны обеспечить надежные вычисления, так как они либо недостаточно управляемы, либо очень подвержены влиянию шумов. Однако физических запретов на построение эффективного квантового компьютера нет, необходимо лишь преодолеть технологические трудности.
2001 г. - корпорация IBM создала управляемый ядерно-магнитным резонансом (ЯМР) квантовый компьютер из 7 кубит, реализующий факторизацию числа 15 посредством алгоритма Шора.
Ноябрь 2009 г. - Создана модель программируемого квантового процессора.
Физики из Национального института стандартов и технологий (США) реализовали обширный набор «программ» на базе двух кубит, представленных ионами бериллия.
Январь 2010 г. - Примитивный квантовый компьютер был использован для расчета энергии молекулы водорода.
Физикам из Гарвардского университета (США) и Университета Квинсленда (Австралия) удалось реализовать алгоритм вычисления энергии основного и возбужденных состояний молекулы Н2, задействовав в экспериментах всего два фотонных кубита.
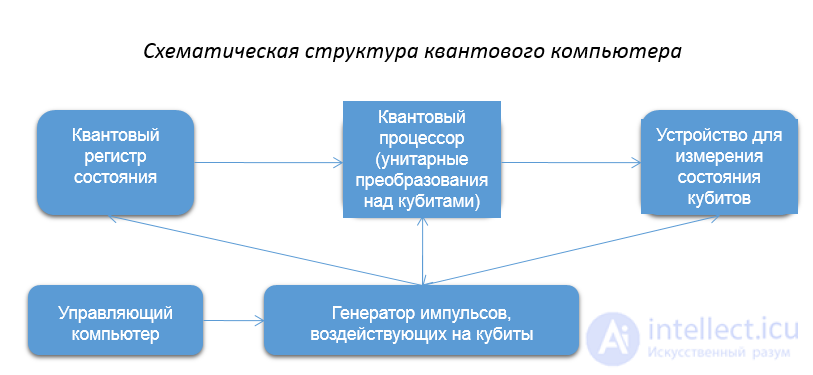
Рис Схематическая структура квантового компьютера
К физической системе, реализующей полномасштабный квантовый компьютер (превосходящий по производительности любой классический компьютер), предъявляются следующие требования:
Идея квантовых вычислений состоит в том, что квантовая система из L двухуровневых квантовых элементов (квантовых битов, кубитов) имеет 2L линейно независимых состояний, а значит, вследствие принципа квантовой суперпозиции, пространство состояний такого квантового регистра является 2L-мернымгильбертовым пространством. Операция в квантовых вычислениях соответствует повороту вектора состояния регистра в этом пространстве. Таким образом, квантовое вычислительное устройство размером L кубит фактически задействует одновременно 2L классических состояний.
Физическими системами, реализующими кубиты, могут быть любые объекты, имеющие два квантовых состояния: поляризационные состояния фотонов, электронные состояния изолированных атомов или ионов, спиновые состояния ядер атомов, и т. д.
Один классический бит может находиться в одном и только в одном из состояний 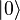 или
или  . Квантовый бит, называемый кубитом, находится в состоянии
. Квантовый бит, называемый кубитом, находится в состоянии  , так что |a|² и |b|² — вероятности получить 0 или 1 соответственно при измерении этого состояния;
, так что |a|² и |b|² — вероятности получить 0 или 1 соответственно при измерении этого состояния;  ; |a|² + |b|² = 1. Сразу после измерения кубит переходит в базовое квантовое состояние, соответствующее классическому результату.
; |a|² + |b|² = 1. Сразу после измерения кубит переходит в базовое квантовое состояние, соответствующее классическому результату.
Пример:
Имеется кубит в квантовом состоянии 
В этом случае, вероятность получить при измерении
| 0 | составляет | (4/5)²=16/25 | = 0,64, |
| 1 | (-3/5)²=9/25 | = 0,36. |
В данном случае, при измерении мы получили 0 с 0,64 вероятностью.
В результате измерения кубит переходит в новое квантовое состояние 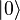 , то есть, при следующем измерении этого кубита мы получим 0 со стопроцентной вероятностью (предполагается, что по умолчанию унитарная операция тождественна; в реальных системах это не всегда так).
, то есть, при следующем измерении этого кубита мы получим 0 со стопроцентной вероятностью (предполагается, что по умолчанию унитарная операция тождественна; в реальных системах это не всегда так).
Приведем для объяснения два примера из квантовой механики: 1) фотон находится в состоянии 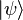 суперпозиции двух поляризаций. Это состояние есть вектор в двумерной плоскости, систему координат в которой можно представлять как две перпендикулярные оси, так что
суперпозиции двух поляризаций. Это состояние есть вектор в двумерной плоскости, систему координат в которой можно представлять как две перпендикулярные оси, так что 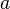 и
и  есть проекции
есть проекции 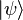 на эти оси; измерение раз и навсегда коллапсирует состояние фотона в одно из состояний
на эти оси; измерение раз и навсегда коллапсирует состояние фотона в одно из состояний 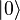 или
или  , причем вероятность коллапса равна квадрату соответствующей проекции. Полная вероятность получается по теореме Пифагора.
, причем вероятность коллапса равна квадрату соответствующей проекции. Полная вероятность получается по теореме Пифагора.
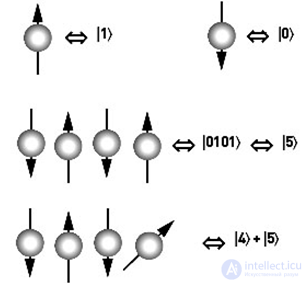
Перейдем к системе из двух кубитов. Измерение каждого из них может дать 0 или 1. Поэтому у системы есть 4 классических состояния: 00, 01, 10 и 11. Аналогичные им базовые квантовые состояния:  . И наконец, общее квантовое состояние системы имеет вид
. И наконец, общее квантовое состояние системы имеет вид 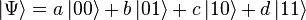 . Теперь |a|² — вероятность измерить 00 и т. д. Отметим, что |a|²+|b|²+|c|²+|d|²=1 как полная вероятность.
. Теперь |a|² — вероятность измерить 00 и т. д. Отметим, что |a|²+|b|²+|c|²+|d|²=1 как полная вероятность.
Если мы измерим только первый кубит квантовой системы, находящейся в состоянии  , у нас получится:
, у нас получится:
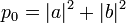 первый кубит перейдет в состояние
первый кубит перейдет в состояние 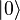 , а второй — в состояние
, а второй — в состояние 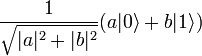 ,
,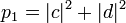 первый кубит перейдет в состояние
первый кубит перейдет в состояние  , а второй — в состояние
, а второй — в состояние 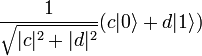 .
.В первом случае измерение даст состояние 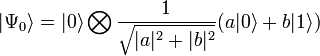 , во втором — состояние
, во втором — состояние 
Мы снова видим, что результат такого измерения невозможно записать как вектор в гильбертовом пространстве состояний. Такое состояние, в котором участвует наше незнание о том, какой же результат получится на первом кубите, называют смешанным состоянием. В нашем случае такое смешанное состояние называют проекцией исходного состояния  на второй кубит, и записывают в виде матрицы плотности вида
на второй кубит, и записывают в виде матрицы плотности вида  где матрица плотности состояния
где матрица плотности состояния 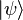 определяется как
определяется как 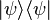 .
.
В общем случае системы из L кубитов, у нее 2L классических состояний (00000…(L-нулей), …00001(L-цифр), … , 11111…(L-единиц)), каждое из которых может быть измерено с вероятностями 0—1.
Таким образом, одна операция над группой кубитов вычисляется сразу над всеми возможными ее значениями, в отличие от группы классических битов, когда может быть использовано лишь одно текущее значение. Это и обеспечивает беспрецедентный параллелизм вычислений.
Упрощенная схема вычисления на квантовом компьютере выглядит так: берется система кубитов, на которой записывается начальное состояние. Затем состояние системы или ее подсистем изменяется посредством унитарных преобразований, выполняющих те или иные логические операции. В конце измеряется значение, и это результат работы компьютера. Роль проводов классического компьютера играют кубиты, а роль логических блоков классического компьютера играют унитарные преобразования. Такая концепция квантового процессора и квантовых логических вентилей была предложена в 1989 году Дэвидом Дойчем. Также Дэвид Дойч в 1995 году нашел универсальный логический блок, с помощью которого можно выполнять любые квантовые вычисления.
Оказывается, что для построения любого вычисления достаточно двух базовых операций. Квантовая система дает результат, только с некоторой вероятностью являющийся правильным. Но за счет небольшого увеличения операций в алгоритме можно сколь угодно приблизить вероятность получения правильного результата к единице.
С помощью базовых квантовых операций можно симулировать работу обычных логических элементов, из которых сделаны обычные компьютеры. Поэтому любую задачу, которая решена сейчас, квантовый компьютер решит, и почти за такое же время. Следовательно, новая схема вычислений будет не слабее нынешней.
Большая часть современных ЭВМ работают по такой же схеме: n бит памяти хранят состояние и каждый такт времени изменяются процессором. В квантовом случае система из n кубитов находится в состоянии, являющимся суперпозицией всех базовых состояний, поэтому изменение системы касаетсявсех 2n базовых состояний одновременно. Теоретически новая схема может работать намного (в экспоненциальное число раз) быстрее классической. Практически (квантовый) алгоритм Гровера поиска в базе данных показывает квадратичный прирост мощности против классических алгоритмов
 за время
за время  .
.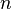 частиц за почти линейное время с использованием
частиц за почти линейное время с использованием  кубит.
кубит.Было показано, что не для всякого алгоритма возможно «квантовое ускорение». Более того, возможность получения квантового ускорения для произвольного классического алгоритма является большой редкостью .
Один кубит можно представить в виде электрона в двухъямном потенциале, так что 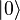 означает нахождение его в левой яме, а
означает нахождение его в левой яме, а  — в правой. Это называется кубит на зарядовых состояниях. Общий вид квантового состояния такого электрона:
— в правой. Это называется кубит на зарядовых состояниях. Общий вид квантового состояния такого электрона:  . Зависимость его от времени есть зависимость от времени амплитуд
. Зависимость его от времени есть зависимость от времени амплитуд  ; она задается уравнением Шредингера вида
; она задается уравнением Шредингера вида  где гамильтониан
где гамильтониан 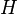 имеет в силу одинакового вида ям и эрмитовости вид
имеет в силу одинакового вида ям и эрмитовости вид  для некоторой константы
для некоторой константы 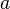 , так что вектор
, так что вектор  есть собственный вектор этого гамильтониана с собственным значением 0 (так называемое основное состояние), а
есть собственный вектор этого гамильтониана с собственным значением 0 (так называемое основное состояние), а  — собственный вектор со значением
— собственный вектор со значением 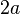 (первое возбужденное состояние). Никаких других собственных состояний (с определенным значением энергии) здесь нет, так как наша задача двумерная. Поскольку каждое состояние
(первое возбужденное состояние). Никаких других собственных состояний (с определенным значением энергии) здесь нет, так как наша задача двумерная. Поскольку каждое состояние  переходит за время
переходит за время 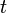 в состояние
в состояние 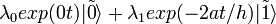 , то для реализации операции NOT (перехода
, то для реализации операции NOT (перехода 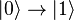 и наоборот достаточно просто подождать время
и наоборот достаточно просто подождать время 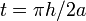 . То есть гейт NOT дается просто естественной квантовой эволюцией нашего кубита при условии, что внешний потенциал задает двухъямную структуру; это делается с помощью технологии квантовых точек.
. То есть гейт NOT дается просто естественной квантовой эволюцией нашего кубита при условии, что внешний потенциал задает двухъямную структуру; это делается с помощью технологии квантовых точек.
Для реализации CNOT надо расположить два кубита (то есть две пары ям) перпендикулярно друг другу, и в каждой из них расположить по отдельному электрону. Об этом говорит сайт https://intellect.icu . Тогда константа 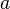 для первой (управляемой) пары ям будет зависеть от того, в каком состоянии находится электрон во второй (управляющей) паре ям: если ближе к первой,
для первой (управляемой) пары ям будет зависеть от того, в каком состоянии находится электрон во второй (управляющей) паре ям: если ближе к первой, 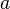 будет больше, если дальше — меньше. Поэтому состояние электрона во второй паре определяет время совершения NOT в первой яме, что позволяет снова выбрать нужную длительность времени для производства операции CNOT.
будет больше, если дальше — меньше. Поэтому состояние электрона во второй паре определяет время совершения NOT в первой яме, что позволяет снова выбрать нужную длительность времени для производства операции CNOT.
Эта схема очень приблизительная и идеализирована; реальные схемы сложнее и их реализация представляет вызов экспериментальной физике.
Алгоритм телепортации реализует точный перенос состояния одного кубита (или системы) на другой. В простейшей схеме используются 3 кубита: телепортируемый кубит и запутанная пара, один кубит которой находится на другой стороне. Отметим, что в результате работы алгоритма первоначальное состояние источника разрушится — это пример действия общего принципа невозможности клонирования — невозможно создать точную копию квантового состояния, не разрушив оригинал. Не получится скопировать произвольное состояние, и телепортация — замена этой операции.
Телепортация позволяет передавать квантовое состояние системы с помощью обычных классических каналов связи. Таким образом, можно, в частности, получить связанное состояние системы, состоящей из подсистем, удаленных на большое расстояние.
Квантовый компьютер (в отличие от обычного) в качестве носителей информации использует квантовые объекты, а для проведения вычислений квантовые объекты должны быть соединены в квантовую систему.
Что же такое квантовый объект?
Квантовый объект — объект микромира (квантового мира), который проявляет квантовые свойства:
- Имеет определенное состояние с двумя граничными уровнями
- Находится в суперпозиции своего состояния до момента измерения
- Запутывается с другими объектами для создания квантовых систем
- Выполняет теорему о запрете клонирования (нельзя скопировать состояние объекта)
Разберем каждое свойство более подробно:
Имеет определенное состояние с двумя граничными уровнями (конечное состояние)
Классический пример из реального мира — монета. У нее есть состояние “сторона”, которая принимает два граничных уровня — “орел” и “решка”.
Находится в суперпозиции своего состояния до момента измерения
Подбросили монетку, она летит и вращается. Пока она вращается невозможно сказать в каком из граничных уровней находится ее состояние “сторона”. Но стоит нам ее прихлопнуть и посмотреть на результат — как суперпозиция состояний тут же схлопывается в одно из двух граничных — “орел” и “решка”. Прихлопывание монетки в нашем случае и есть измерение.
Запутывается с другими объектами для создания квантовых систем
С монеткой сложно, но попробуем. Представьте мы подбросили три монетки так, что они вращаются цепляясь друг за друга, такое жонглирование монетками. В каждый момент времени не только каждая из них находится в суперпозиции состояний, но эти состояния взаимно влияют друг на друга (монетки же сталкиваются).
Выполняет теорему о запрете клонирования (нельзя скопировать состояние объекта)
Пока монетки летят и вращаются, мы никаким образом не можем создать отдельную от системы копию вращающегося состояния любой из монеток. Система живет сама в себе и очень ревностно относится к тому, чтобы выдать наружу какую-либо информацию.
Еще пара слов о самом понятии “суперпозиции”, практически во всех статьях суперпозицию объясняют как “находится во всех состояниях одновременно”, что, конечно, верно, но временами излишне запутывает. Суперпозицию состояний можно представить себе также как то, что в каждый момент времени у квантового объекта есть определенные вероятности схлопнуться в каждый из своих граничных уровней, и в сумме эти вероятности, естественно, равны 1. Далее при рассмотрении кубита мы остановимся на этом более подробно.
Для монеток это можно себе представить визуально — в зависимости от начальной скорости, угла подброса, состояния окружающей среды, в которой летит монетка, в каждый момент времени вероятность получить “орел” или “решку” разная. И, как говорилось ранее, состояние такой летящей монетки можно себе представить как “находится во всех своих граничных состояниях одновременно, но с разной вероятностью их реализации”.
Любой объект, для которого выполняются вышеуказанные свойства и который мы можем создать и управлять, может использоваться как носитель информации в квантовом компьютере.
Чуть дальше мы поговорим о текущем состоянии дел с физической реализацией
продолжение следует...
Часть 1 Квантовый компьютер понятие и применение проблемы и перспективы
Часть 2 Алгоритм Шора. - Квантовый компьютер понятие и применение проблемы и
Часть 3 Декогеренция - Квантовый компьютер понятие и применение проблемы и перспективы
Выводы из данной статьи про квантовый компьютер указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое квантовый компьютер , квантовые алгоритмы, квантовое превосходство и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Квантовая информатика
Комментарии
Оставить комментарий
Квантовая информатика
Термины: Квантовая информатика