7.1 Измерение параметров компонентов с сосредоточенными параметрами

Привет, Вы узнаете о том , что такое измерение параметров компонентов с сосредоточенными параметрами, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое измерение параметров компонентов с сосредоточенными параметрами , настоятельно рекомендую прочитать все из категории МЕТРОЛОГИЯ И ЭЛЕКТРОРАДИОИЗМЕРЕНИЯ.

7

Измерение параметров компонентов электрорадиотехнических цепей

 

Тема 7.1 измерение параметров компонентов с сосредоточенными параметрами

7.1.1 Общие сведения

Радиотехнические цепи, физические размеры которых гораздо меньше рабочей длины волны, называют цепями с сосредоточенными параметрами. Свойства таких цепей практически не зависят от конфигурации выводов (электродов) активных и пассивных элементов и размеров соединительных проводов. Радиотехнические цепи, физические размеры которых соизмеримы с рабочей длиной волны колебаний, относятся к цепям с распределенными параметрами. Каждый элемент или соединительный провод этой цепи обладает сопротивлением (активными, т.е. невозвратимыми, потерями мощности), индуктивностью и емкостью. Подобные цепи называют длинными линиями или СВЧ-трактами.

Элементы радиотехнической цепи можно соединить в двухполюсники и четырехполюсники. Двухполюсник (одиночный элемент или сложная электрическая цепь) имеет два вывода - полюса; четырехполюсник - пару входных и пару выходных выводов - четыре полюса.

В электрических цепях с сосредоточенными параметрами широко применяют линейные компоненты общего назначения: резисторы, катушки индуктивности и конденсаторы. При определенных допущениях эти элементы рассматривают как линейные пассивные двухполюсники, характеризуемые некими идеальными параметрами - сопротивлением R (величина, обратная сопротивлению - проводимость Y), индуктивностью L,емкостью С.

При измерениях не всегда удается определить значение того или иного параметра, соответствующее идеальному виду элемента. Несовершенство конструкции и характеристик применяемых материалов является причиной появления паразитных параметров элементов. Так, наряду с главным параметром резистора - активным сопротивлением, он имеет и определенную индуктивность; катушка индуктивности, обладая индуктивностью, имеет паразитную емкость и активное сопротивление (сопротивление потерь) и т.д.

С учетом паразитных параметров резистор, конденсатор или катушку индуктивности можно соответственно характеризовать некоторым эффективным значением сопротивления, емкости, индуктивности, которые зависят от частоты протекающих по ним токов. Поэтому эффективные параметры компонентов необходимо измерять на рабочих частотах, если их влиянием на результат измерения нельзя пренебречь. Необходимо еще знать и ряд вторичных параметров этих элементов, например: добротность Q

катушки индуктивности, тангенс угла потерь δ конденсатора, характеристическое сопротивление ρ контура, что позволяет более точно определять измеряемые параметры.

Параметрами длинных линий, по аналогии с цепями с сосредоточенными постоянными, являются погонные активное сопротивление, индуктивность и емкость. Однако в отличие от цепей с сосредоточенными постоянными, эти параметры не имеют такого четкого физического смысла и поэтому их не измеряют. В то же время элементы СВЧ-трактов служат аналогами двух - и четырехполюсников, из которых состоят цепи с сосредоточенными постоянными. Эта аналогия позволяет рассматривать параметры: КВЧ-трактов как параметры двух - и четырехполюсников.

 

 

7.1.2 Измерение активных сопротивлений методом амперметра и вольтметра

Измерение методом амперметра и вольтметра сводится к определению тока или напряжения в цепи с измеряемым двухполюсником и последующему расчету его параметров по закону Ома. Метод можно использовать для измерения активного и полного сопротивления, индуктивности и емкости. На рис. 7.1 показана структурная реализация этих методов при измерениях активного сопротивления. Измерение активных сопротивлений проводят на постоянном токе, при этом включать резистор Rx в измерительную цепь можно по двум схемам. 

 

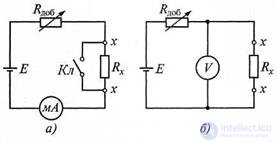
Рисунок 7.1 Измерение активных сопротивлений методом: а - амперметра; б - вольтметра

В          схеме          с        амперметром      (рис. 7.1,а)      отклонение          показаний миллиамперметра пропорционально току

                                               I = RдобE+ Rх ,                                   (7.1)

и обратно пропорционально измеряемому сопротивлению Rx. По такой схеме измеряют достаточно большие сопротивления (от 1 Ом до 200 МОм). Перед измерениями зажимы х замыкают ключом Кл (тем самым закорачивают резистор Rx) и переменным резистором Rдо6 устанавливают такой ток, чтобы стрелка отклонилась на всю шкалу, что соответствует точке 0 Ом.

Для      измерения небольших          сопротивлений   (0,01...100       Ом) используют схему с вольтметром (рис. 7.1,б). Показания вольтметра определяют по формуле:

                                   U =ERдобR+x Rx ,                                         (7.2)

при условии, что Rдо5 >> Rх, U ≈ ERх/Rдоб, т.е. имеет место прямая зависимость напряжения (показания вольтметра) от измеряемого сопротивления Rх. Перед измерением стрелку на приборе совмещают с отметкой «∞» при разомкнутых зажимах х.

Обе схемы приводят к методическим погрешностям измерения ΔRX, зависящим от внутренних сопротивлений приборов. Очевидно, что в схеме, изображенной на рис. 7.1,а, методическая погрешность измерения тем меньше, чем меньше внутреннее сопротивление амперметра (при R А ->0, ΔRх >0), а в схеме, показанной на рис. 7.1,б, эта погрешность тем меньше, чем больше внутреннее сопротивление вольтметра (при Rv -> ∞, ΔRx —> 0). Итак, схемой, показанной на рис. 7.1,а, следует пользоваться для измерения больших сопротивлений, а схемой, показанной на рис. 7.1,б, - для измерения малых сопротивлений. Точность обоих методов невысока - погрешность измерения составляет 1,5...2 %.

 

7.1.3 Омметры

Омметром называют прямо показывающий прибор для измерения электрического сопротивления на постоянном токе.

Действие омметра основано на применении закона Ома: измеряется падение напряжения на неизвестном сопротивлении при заданном токе или измеряется ток через неизвестное сопротивление при определенном напряжении. В простейших омметрах в качестве отсчетного устройства используется магнитоэлектрический механизм достаточной чувствительности (ток полного отклонения IК = 50 ... 100мкА). Различают омметры с последовательным и параллельным включением измеряемого сопротивления. Принципиальная электрическая схема омметра последовательного типа изображена на рис. 7.2 При коротком замыкании выводов А и В переменным резистором Rдоб устанавливают в цепи такой ток, чтобы стрелка прибора РА1 отклонилась на всю шкалу. Это - «нуль омметра». При присоединении к выводам АВ измеряемого сопротивления Rx установленный ранее ток уменьшится и стрелка прибора займет другое положение.  

 

  

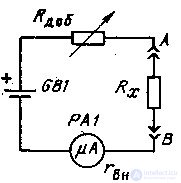
Рисунок 7.2 Схема омметра. 

Если обозначить относительную величину отклонения стрелки прибора а=I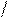Ik . а отношение измеряемого сопротивления к внутреннему сопротивлению омметра через А = RX/ROM, то выражение а = 1/(1 + А) определит уравнение шкалы омметра (рис. 7.3). Из приведенного выражения видно, что при бесконечно большом сопротивлении Rх (разрыв цепи) А→∞, а→ 0, ток равен нулю и стрелка прибора не отклоняется. Это положение стрелки на шкале отмечается знаком ∞. То, что на шкале рассматриваемого омметра имеются отметки 0 и ∞, не означает, что им можно измерять любое сопротивление. Шкала прибора по краям сильно сжата и практически используется лишь ее Средняя часть. Середина шкалы омметра соответствует его входному сопротивлению (при Rx = R0M, а = 0,5). Это сопротивление и определяет пределы сопротивлений, измеряемых прибором.

Обычно Rx лежит а пределах от 0,01ROM до 100Rом. Если задан верхний R в и нижний Rн пределы измерения сопротивления по данной шкале омметра, то

Рисунок 7.3 Шкала омметра.

 

Погрешность измерений:    δr =∆A/ A=±k (1+А)2               (7.3)

где k — относительная приведенная погрешность (класс точности

прибора РА1).

Измеряемое сопротивление может включаться не только последовательно, но и параллельно микроамперметру. В этом случае шкала прибора получается не обратной, а прямой: «нуль» — слева, а «∞» — справа, но по-прежнему нелинейной. Ток через прибор P1:

                                                                                                                Iизм=IRx/(Rx+rвн)                                    (7.4)

 Приняв во внимание, что общий ток в цепи I= E/Rдоб+Rxrвн ./(Rx+rвн) можно получить:

                                                                                                               Iизм=Е/Rдоб+rвн+ rвнRдоб/Rx                (7.5)

Омметрами с прямой шкалой удобнее измерять сопротивления, соизмеримые с внутренним сопротивлением rвн прибора, т. е. меньшие, чем омметрами с обратной шкалой.

Для расширения диапазона измерений применяют многопредельные омметры. Для этого изменяют значение сопротивления Rдоб в 10, 100, 1000 раз, К многопредельным относятся M212, М371, а также омметры, входящие в состав универсальных приборов. При измерении больших сопротивлений приходится увеличивать напряжение питания.

 

7.1.4 Измерение с помощью логометра

Уменьшить влияние источника питания Е на точность изменения активных сопротивлений позволяет применение магнитоэлектрического прибора - логометра, встречающегося в лабораторной измерительной практике. Устройство и схема включения магнитоэлектрического логометра представлены на рис. 7.6.

Логометр содержит две жестко скрепленных между собой рамки, помещенные в неравномерное поле постоянного магнита (рис. 7.6,а), которое реализуется за счет специальной конфигурации полюсных наконечников. Неравномерным поле создают для того, чтобы вращающие моменты, приложенные к рамкам, зависели не только от токов, протекающих в рамках, но и от положения рамок в магнитном поле, т.е. М1 = ψ1(α)I1; М2 = ψ2(α)Ix, где I1 , IХ

- токи, протекающие в рамках; ψ1(α), ψ2(α) - значения

 

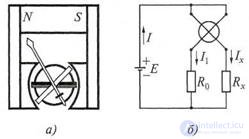
Рисунок 7.6 Магнитоэлектрический логометр:

а - устройство; б - схема включения

 

потокосцеплений магнитов с их рамками. Положение равновесия наступит при М1 = М 2;ψ1(α)I1=ψ2(α)Ix и, следовательно, угол отклонения подвижной системы определится как

                                                  α= F(I1/Ix) ,                                          (7.3)

Для схемы, приведенной на рис. 7.6,б

                                                                                                  E                      E              FRp +Rx 

                        I1 = Rp + R0 ; Ix = Rp + Rx ;α= Rp +R0  ,                  (7.4)

где Rр - сопротивление рамок; RQ - образцовое сопротивление. Итак согласно (10.4), показания логометра не зависят от колебания напряжения питания. Зависимость показаний от Rх позволяет создавать лабораторные логометры с погрешностью измерений, не превышающей 0,5 %. Нечувствительность логометра к колебаниям напряжения питания позволила также разработать класс приборов, питающихся от генераторов, ротор которых вращают вручную и еще иногда использующиеся для определения сопротивления изоляции телефонных сетей и на производстве.

 

7.1.5 Электронные омметры

Электронные омметры аналогового типа выполняют на основе инвертирующего усилителя на ОУ, охваченного отрицательной обратной связью с помощью измеряемого сопротивления Rх (рис. 7.7). Об этом говорит сайт https://intellect.icu . Напряжение на выходе усилителя омметра нетрудно вычислить по формуле:

                                                     Uвых =−URR1x ,                                                   (7.5) 

 

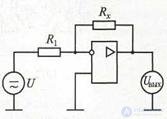
Рисунок 7.7 Схема электронного омметра

 

Поскольку выходное напряжение в схеме линейно связано с измеряемым сопротивлением Rх, то шкала прибора может быть проградуирована непосредственно в единицах сопротивления. Шкала получается равномерной в широких пределах и практически не зависит от внешних (навесных) элементов усилителя. Погрешности измерения электронных омметров значительные - 2...4 %.

В приборах для измерения особо больших активных сопротивлений (тераомметрах) сопротивления Rх и R1 меняют местами, при этом шкала измерительного прибора получается обратной и напряжение

                                                     Uвых =−URR1х ,                                                 (7.6)

Погрешность измерения сопротивлений тераомметрами достигает 10 %.

Электронные         измерители         сопротивлений,       построенные       по приведенным схемам, используют для измерения сопротивлений и на переменном токе.

 

7.1.6 Мостовые измерители параметров элементов

Для измерения параметров элементов цепей методом сравнения применяют мосты.

Сравнение измеряемой величины (сопротивления, индуктивности, емкости) с образцовой мерой при помощи моста в процессе измерения осуществляют вручную или автоматически, на постоянном или переменном токе.

Мостовые схемы обладают высокой чувствительностью, большой точностью, широким диапазоном измеряемых значений параметров элементов. На основе мостовых методов строят средства измерения, предназначенные как для измерения какой - либо одной величины, так и универсальные аналоговые и цифровые приборы.

 

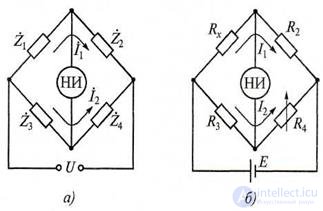
Рисунок 7.8 Схемы четырехплечих мостов:

а - обобщенная; б - для измерения активных сопротивлений НИ - нуль-индикатор 

Существует несколько разновидностей мостовых схем измерения параметров R, L, С: четырехплечие, уравновешенные, неуравновешенные и процентные. Управление этими мостами может осуществляться как вручную, так и автоматически. Наибольшее распространение получили схемы четырехплечих уравновешенных мостов (рис. 7.8). Обобщенная структурная схема такого моста показана на рис. 7.8,а. Сопротивления четырехплечего моста в общем случае имеют комплексный характер.

Условия равновесия четырехплечего моста определяются равенствами:

 

                                                                     Z1 Z4 = Z2 Z3,                                                           (7.7) 

                                                   φ1 + φ4 = φ2 + φ3,                                                                      (7.8)

где Z1, Z2, Z3, Z4 - модули комплексных сопротивлений; φ1, φ2, φ3, φ4 - их

соответствующие фазы.

Для выполнения этих равенств необходимо наличие в плечах моста элементов с регулируемыми параметрами. Для обеспечения условия равенства   амплитуд   (7.7) наиболее    удобно       применять       эталонное регулируемое активное сопротивление. Элементом, обеспечивающим условие равновесия фаз (7.8), служит эталонный конденсатор емкостью Со с малыми потерями.

Схема четырехплечего уравновешенного моста постоянного тока для измерений активных сопротивлений представлена на рис. 7.8,б.Электронный или цифровой нуль-индикатор НИ включают в диагональ уравновешенного моста. Ток в диагонали моста в момент измерения активного сопротивления устанавливают равным нулю. Для равновесия моста необходимо, чтобы выполнялось равенство RXR4 = R2Rз откуда неизвестное сопротивление

                                                Rx =R2 RR34 ,                                       (7.9)

Для достижения равновесия моста с активными сопротивлениями достаточно иметь один регулируемый параметр (например, сопротивление резистора R4), как показано на рис. 7.8,б. Пределы измеряемых сопротивлений для этих мостов составляют от 10 -2 до 107 Ом; погрешности измерения - от долей процента до нескольких процентов в зависимости от диапазона измерения.

Показанная на рис. 7.8,б схема моста может быть частично реализована на цифровых элементах. Для этого регулируемый резистор изготавливают в виде набора сопротивлений, выполненных в соответствии с двоично-десятичным кодом. Сопротивления поочередно включают в плечо измерительного моста до тex пор, пока мост не уравновесится. Положение ключей характеризует собой код измеряемой величины, поступающий затем на цифровое отсчетное устройство.

Ряд схем мостов на переменном токе для измерения индуктивности и добротности катушек представлен на рис. 7.9. В них используют источники гармонического тока с напряжением U и угловой частотой ω. Эти четырехплечие мосты обеспечивают наилучшее уравновешивание. Эквивалентные схемы замещения для катушек индуктивности с потерями могут быть последовательными или параллельными в зависимости от потерь, отраженных активным сопротивлением.

 

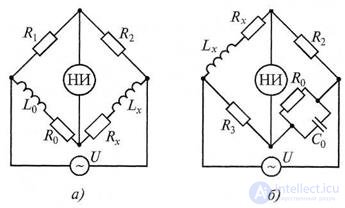
Рисунок 7.9 Схемы мостов для измерения индуктивностей и их добротностей с образцовыми элементами:

а — катушкой; б — конденсатором

Условие равновесия четырехплечего моста для схемы, показанной на рис. 7.9,а, имеет вид:

                                         R1(Rx + jωLx) = R2(R0 + jωL0),                               (7.9)

где Lx и Rx - измеряемые индуктивность и сопротивление омических

потерь в катушке; Lo и R0 - образцовые индуктивность и сопротивление.

Приравняв действительные и мнимые члены формулы (7.9) получим:

                                            Lx = L0R2/R1; Rx = RoR2/R1,                                 (7.10)

Поскольку изготовление высокодобротных образцовых катушек вызывает определенные трудности, часто в качестве образцовой меры в мостах переменного тока применяют конденсатор (рис. 7.9,б). Для этой схемы

                                          Rx + jωLx = R2R3(l/R0 + jωC0),                               (7.11)

Если в данном уравнении приравнять отдельно вещественную и мнимую части, то получим следующие выражения для определения параметров катушки индуктивности:

                                            RX = R2R3/R0; Lх = CoR2R3,                                 (7.12)

Добротность катушки:

                                                 Qx = ωLx/Rx = R0ωC0,                                     (7.13)

Для измерения емкости и тангенса угла потерь конденсаторов с достаточно малыми потерями применяют мостовую схему, представленную на рис. 7.10,а (последовательное соединение элементов Cx и Rx), а с большими потерями - на рис. 7.10,б (параллельное соединение элементов Сх и Rx).

 

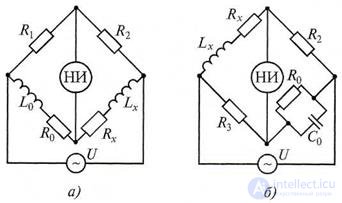
Рисунок 7.10 Схемы мостов для измерения емкости и тангенса угла потерь: а - с малыми потерями; б - с большими потерями

 

Условие равновесия для схемы, показанной на рис. 7.10,а, имеет вид:

                                      R4[RX + 1/(jωСx)] = R2[Ro + 1/(jωС0)],                       (7.14)

Разделив вещественную и мнимую части последнего выражения, получаем следующие формулы для определения параметров конденсатора:

                                           Cх = C0R4/R2; Rx = R2R0/R4,                                  (7.15)

Тангенс угла потерь конденсатора:

                                               tgδх = ωCхRx = ωC0R0,                                                           (7.16)

Для моста с параллельным соединением элементов Сх и Rx (см. рис.

7.10,б) условие равновесия имеет следующий вид:

                                R4Rx(1 + jωC0R0) = R2R0(1 + jωCxRx),                             (7.17)

Отсюда

                    Сх = C0R4/R2; Rx = R2R0/R4,                                (7.18)

Тангенс угла потерь конденсатора при параллельной схеме его замещения:

                                         tg δ = 1/(ωСхRх) = 1/(ωС0R0),                               (7.19)

Уравновешивание схем обеспечивают поочередным регулированием переменных образцовых сопротивлений или емкостей. Эту процедуру называют шагами, а количество шагов определяет сходимость моста. Мост с хорошей сходимостью имеет не более пяти шагов.

Мосты переменного тока используют на низких частотах: 500...5000 Гц. При работе на повышенных частотах погрешности измерения резко возрастают. Погрешность измерений моста переменного тока определяют погрешности элементов образующий мост, переходных сопротивлений контактов и чувствительность схемы. Мосты переменного тока больше чем мосты постоянного тока подвержены влиянию помех и паразитных связей между плечами, плечами и землей и т.д. Поэтому, даже при тщательном экранировании моста и принятии других мер защиты, погрешности у мостов переменного тока больше, чем у мостов постоянного тока.

 

7.1.7 Резонансный метод измерения параметров элемента

Резонансный метод измерения основан на настройке в резонанс колебательного контура, включающего образцовый и измеряемый элементы (индуктивности или емкости), и определении его резонансной частоты. Метод применяют для измерения индуктивностей и емкостей на высоких частотах, так как в области низких частот резонансные явления проявляются недостаточно резко, что не позволяет получить высокую точность измерения.

С помощью резонансных схем осуществляют измерение путем замещения, при котором один и тог же эффект (например, резонанс на фиксированной частоте) повторяют дважды: первый раз - с измеряемым элементом, второй - с мерой той же физической природы. За результат измерения принимают значение, равное величине меры при резонансе. Резонансные схемы удобны при точных измерениях относительно малых значений индуктивностей и взаимной индуктивности, емкостей и т.д.

 

 

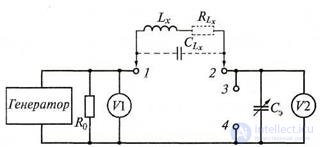
Рисунок 7.11 Упрощенная структурная схема куметра

 

Наиболее универсальным прибором для измерения параметров цепей резонансным методом является куметр (от          латинской буквы      Q -

характеристики добротности катушки индуктивности), в котором основной измерительной цепью служит последовательный резонансный контур. Упрощенная структурная схема куметра показана на рис. 7.11. Источником синусоидальных сигналов, подаваемых на последовательный резонансный контур, является генератор тока, нагруженный на малое активное сопротивление Ro ≈ 0,05 Ом. Частота выходных колебаний генератора может изменяться в широких пределах.

Уровень входного сигнала необходимо поддерживать постоянным (что контролируют по вольтметру V1).

При измерении индуктивности исследуемую катушку подключают к зажимам 1, 2. При этом резонансный контур будет образован катушкой измеряемой индуктивности Lx с активными потерями RLx и межвитковой емкостью ее проводов СLx а также перестраиваемой эталонной емкостью Сэ. Резонанс в контуре на заданной частоте устанавливают изменением величины емкости Сэ, эталонного конденсатора. Состояние резонанса контура определяют по вольтметру V2, отградуированному в значениях добротности Q. Измерение индуктивности Lx с учетом емкости СLx проводят на двух резонансных частотах, которые равны:

fp1 = 2π Lx(C1э C ; fp2 = 2π Lx(C1э2 +CLx) ,   (7.20) 1 + Lx)

где Сэ1 и Сэ2 - эталонные емкости на частотах fр1 и fр2.

Пусть соотношение частот fр1 = Кfр2, где коэффициент К -  вещественное  число. Тогда совместное решение уравнений (7.20) позволяет вычислить ранее неизвестные значения параметров Lx и CLx по формулам:

          Lx = (2πfp1)K2(2C−э21−Сэ1) ; СLx =Cэ2K−2С−э11K2 ,       (7.21)

С помощью куметра можно также определять неизвестные параметры R, С, tgδc, подключая измеряемые резистор или конденсатор к зажимам 3, 4.

Погрешности измерения куметром параметров L, С, tgδc, К в зависимости от используемой схемы составляют 1...5 %. Причинами появления этих погрешностей являются: нестабильность генератора, наличие в контуре сопротивления Ro, неточность шкалы конденсатора эталонной емкости Сэ, погрешности измерительных приборов V1, V2, погрешность считывания показаний.

7.1.8 Цифровые средства измерения параметров элементов

Цифровые средства измерения параметров элементов электрических цепей чаще всего используют сочетание аналогового преобразователя, преобразующего определяемый параметр элемента в активную величину, и соответствующего цифрового прибора для измерения этой величины. Одним из методов измерения сопротивления, индуктивности и емкости является метод прямого

продолжение следует...

Продолжение:

Часть 1 7.1 Измерение параметров компонентов с сосредоточенными параметрами
Часть 2 Контрольные вопросы: - 7.1 Измерение параметров компонентов с сосредоточенными параметрами

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.