Лекция
Привет, Вы узнаете о том , что такое идеальный газ, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое идеальный газ , настоятельно рекомендую прочитать все из категории Молекулярная физика и термодинамика.
В нашем курсе мы постепенно продвигаемся от простого к сложному. До сих пор мы занимались в основном поведением одной частицы в разных силовых полях и свойствами этих полей. Но реальные физические системы состоят из невообразимо большого числа частиц, так что проследить за движением каждой из них не под силу самым мощным компьютерам. Таким (макроскопическим) системам и посвящен в целом весь данный раздел.
Как это чаще всего и бывает в физике, и не только в физике, мы не можем в данный момент, в самом начале, сформулировать критерий макроскопичности системы. Например, в ядре основного изотопа урана 238 нуклонов, так это макроскопически много или нет? Современные суперкомпьютеры способны за разумное время решить динамическую (на базе уравнений квантовой механики) задачу о поведении такого количества частиц. А если этих частиц NA = 6·1023 как в одном моле идеального газа? Легко оценить, сколько времени потребуется многопроцессорному суперкомпьютеру с быстродействием 1015 операций в секунду (быстродействие в 1 терафлоп) на вычисление суммарной кинетической энергии поступательного движения молекул этого газа по формуле
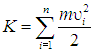 .
.
Вычисляя каждое слагаемое необходимо выполнить два умножения и деление, пренебрегая различиями в продолжительности выполнения этих операций, будем считать, что их просто три. Тогда всего операций при вычислении этой суммы примерно 1,8·1024, на это потребуется 1,8·109 секунд, то есть более 50 лет. И это притом, что, если температура газа известна и равна T, то ответ, с относительной погрешностью не более 10–10 %, имеет вид

где R — универсальная газовая постоянная. Остается выяснить, что такое температура, откуда берется столь малая погрешность, всегда ли она столь мала и много других вопросов, которым и посвящен данный раздел курса.
В науке сложились два метода изучения свойств вещества и физических явлений, связанных с изменением свойств макроскопических тел: молекулярно-кинетический и термодинамический. Оба метода дополняют друг друга. В этом разделе мы сосредоточимся на молекулярно-кинетическом подходе.
Молекулярно-кинетический подход. Молекулярная физика исходит из двух основных положений:
В первом пункте, в качестве частиц, из которых может состоять вещество, кроме электрически нейтральных атомов и молекул упомянуты электрически заряженные частицы — ионы. Прежде всего, это весьма важный случай плазменного состояния вещества. По имеющимся оценкам примерно 95 % видимого вещества во Вселенной находится именно в плазменном состоянии. Кроме того, в растворах — например, поваренной соли 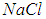 в воде — растворенное вещество существует в виде ионов
в воде — растворенное вещество существует в виде ионов 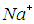 и
и 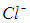 , далее, металлы — это совокупность положительных ионов, колеблющихся около положений равновесия (узлов кристаллической решетки) и свободных электронов, образующих электронный газ. В дальнейшем основное внимание будет уделено «обычному»", состоянию вещества, когда составляющие его частицы электронейтральны. Плазма, как особое состояние вещества, растворы и металлы будут рассмотрены отдельно. Во втором пункте указано: "в беспорядочном хаотическом движении, которое в отсутствие внешних силовых воздействий не имеет какого-либо преимущественного направления". Отметим по этому поводу следующее: в анизотропных кристаллах существуют выделенные направления, обусловленные взаимодействием частиц, составляющих кристалл, и не связанные с внешними силовыми полями. Рассмотрение такого рода ситуаций выходит за рамки данной главы.
, далее, металлы — это совокупность положительных ионов, колеблющихся около положений равновесия (узлов кристаллической решетки) и свободных электронов, образующих электронный газ. В дальнейшем основное внимание будет уделено «обычному»", состоянию вещества, когда составляющие его частицы электронейтральны. Плазма, как особое состояние вещества, растворы и металлы будут рассмотрены отдельно. Во втором пункте указано: "в беспорядочном хаотическом движении, которое в отсутствие внешних силовых воздействий не имеет какого-либо преимущественного направления". Отметим по этому поводу следующее: в анизотропных кристаллах существуют выделенные направления, обусловленные взаимодействием частиц, составляющих кристалл, и не связанные с внешними силовыми полями. Рассмотрение такого рода ситуаций выходит за рамки данной главы.
Молекулярно-кинетическая теория ставит перед собой цель истолковать те свойства вещества, которые непосредственно наблюдаются на опыте (вязкость, теплопроводность и т. п.) как суммарный результат действия молекул. При этом она пользуется статистическим методом, интересуясь не движением каждой отдельной молекулы, но лишь такими средними величинами, которые характеризуют движение и взаимодействие всей совокупности молекул. Молекулярно-кинетическая теория оперирует при этом основными закономерностями физики, действующими на микроскопическом уровне — законами классической механики, электродинамики и др. Поэтому она в состоянии предсказать величины многих физических параметров системы на основе, как говорят, первых принципов. В этой главе мы займемся выводом хорошо известных законов для идеальных газов на основе молекулярно-кинетической теории.
Состояние системы. В любом разделе физики изучение явлений начинается с выделения совокупности тел, которую называют системой.
|
Система — это выделенная определенная совокупность физических тел. Окружающая среда 3 это все тела, которые не входят в систему, но могут влиять на ее свойства и поведение. |
Представим, например, газ (система) в закрытом цилиндре под поршнем (среда), рис. 1.1.

Рис. 1.1. Газ в закрытом цилиндре под поршнем
Видео 1.1. Давление газа: мы Вас приветствуем!
Видео 1.2. Давление газа на стенку сосуда обусловлено столкновениями молекул со стенкой.
Изменение положения поршня или температуры стенок цилиндра меняет состояние системы.
|
Параметры системы — это величины, характеризующие состояние системы. |
Состояние таких простейших систем, как газ, характеризуется следующими макроскопическими параметрами: объемом  , давлением
, давлением 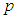 , температурой
, температурой 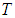 . Естественно, нужны также параметры, определяющие систему — ее масса m, относительная молекулярная масса М (или масса моля m).
. Естественно, нужны также параметры, определяющие систему — ее масса m, относительная молекулярная масса М (или масса моля m).
Итого, четыре величины: объем 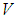 , давление
, давление 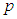 , температура
, температура 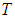 , масса
, масса 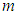 . Или, при известной массе моля вещества системы
. Или, при известной массе моля вещества системы 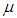 , число молей
, число молей 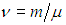 . Если система представляет собой смесь различных веществ, то необходимо добавить относительные концентрации компонент смеси:
. Если система представляет собой смесь различных веществ, то необходимо добавить относительные концентрации компонент смеси: 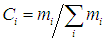 , здесь
, здесь 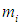 — масса
— масса 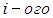 вещества. Очевидно, что в последнем случае параметров не четыре, а больше.
вещества. Очевидно, что в последнем случае параметров не четыре, а больше.
Напомним, что
|
Относительная молекулярная масса М — это безразмерная величина, равная отношению массы молекулы данного вещества к 1/12 массы атома углерода 12С. |
|
Моль — это количество данного вещества, масса которого, выраженная в граммах, численно равна относительной молекулярной массе. |
Другое — эквивалентное — определение моля гласит:
|
Моль — количество вещества системы, которое содержит столько же частиц, сколько атомов содержится в 0,012 килограммах углерода-12. |
Отметим, что современное определение числа Авогадро гласит, что число Авогадро 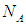 равно числу атомов изотопа 12C, содержащихся в 0,012 килограммах углерода-12. Таким образом, моль можно определить и так:
равно числу атомов изотопа 12C, содержащихся в 0,012 килограммах углерода-12. Таким образом, моль можно определить и так:
|
Моль — количество вещества, которое содержит число Авогадро
|
|
Масса моля (молярная масса m) имеет в СИ размерность кг/моль. |
При решении задач значения относительной молекулярной массы М элементов берутся из таблицы Менделеева. Молярная масса рассчитывается легко:

Например, для золота
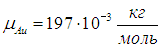
Для сложных веществ необходимо произвести простые арифметические действия, например, для углекислого газа  :
:
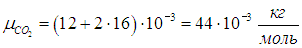
Вообще говоря, такие параметры системы как давление, температура, плотность вещества 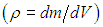 могут иметь разные значения в различных ее точках. В этом случае системе в целом нельзя приписать определенные значения этих параметров, система находится в неравновесном состоянии. Опыт показывает, однако, что если внешние условия неизменны, то система с течением времени приходит в равновесное состояние: выравниваются давления и температуры ее отдельных частей, так что параметры системы принимают определенные значения, остающиеся постоянными сколь угодно долго. При этом внешние условия должны быть таковы, чтобы в системе не было переноса вещества, энергии, импульса и т. п.
могут иметь разные значения в различных ее точках. В этом случае системе в целом нельзя приписать определенные значения этих параметров, система находится в неравновесном состоянии. Опыт показывает, однако, что если внешние условия неизменны, то система с течением времени приходит в равновесное состояние: выравниваются давления и температуры ее отдельных частей, так что параметры системы принимают определенные значения, остающиеся постоянными сколь угодно долго. При этом внешние условия должны быть таковы, чтобы в системе не было переноса вещества, энергии, импульса и т. п.
Рассмотрим, для простоты, систему, суммарная масса которой неизменна, неизменен ее состав и относительные концентрации составляющих ее веществ. Это имеет место, например, в том случае, когда в системе не идут химические реакции. При более общем подходе: в системе нет процессов рождения и уничтожения составляющих ее частиц. Например, реакцию образования молекул воды из молекул кислорода и водорода
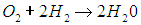
можно рассматривать как процесс уничтожения частиц 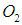 и
и 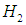 и рождения частиц
и рождения частиц 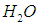 . В ряде случаев, например, в газе фотонов (тепловое излучение) наличие процессов рождения у уничтожения частиц принципиально важно.
. В ряде случаев, например, в газе фотонов (тепловое излучение) наличие процессов рождения у уничтожения частиц принципиально важно.
Дополнительная информация
http://www.femto.com.ua/articles/part_2/4471.html — Физическая энциклопедия. Химический потенциал: физическая величина, необходимая для описания свойств термодинамических систем с переменным числом частиц;
http://www.femto.com.ua/articles/part_1/0017.html — Физическая энциклопедия. Закон Авогадро;
http://marklv.narod.ru/mkt/mkt.htm — Школьный урок с картинками по молекулярно-кинетической гипотезе;
Как будет видно в дальнейшем, для полного описания равновесного состояния такой системы достаточно всего трех параметров: 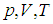 . При этом, если состояние равновесно, то между этими тремя параметрами существует связь: заданные два параметра системы (например, ее температура и объем) однозначно определяют третий (в данном случае давление). Математически эту связь можно охарактеризовать уравнением состояния системы
. При этом, если состояние равновесно, то между этими тремя параметрами существует связь: заданные два параметра системы (например, ее температура и объем) однозначно определяют третий (в данном случае давление). Математически эту связь можно охарактеризовать уравнением состояния системы
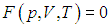 ,
,
где конкретный вид функции F зависит от свойств системы. Примером служат уравнения Клапейрона — Менделеева для идеального или Ван-дер-Ваальса для неидеального газов (эти уравнения будут рассмотрены далее).
Таким образом, у равновесной системы с неизменными массой, составом и относительными концентрациями составляющих ее веществ — в дальнейшем мы не будем это каждый раз оговаривать — независимых параметров всего два и ее равновесное состояние может быть изображено графически точкой на плоскости (рис. 1.2), где по осям отложены какие-нибудь два из трех параметров —  ,
, 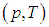 или
или 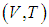 :
:

Рис. 1.2. Равновесные состояния системы на диаграммах (р, V), (р, T) и (V, Т)
|
Процесс — это всякий переход системы из одного состояния в другое. |
Процесс всегда связан с нарушением термодинамической равновесности состояния системы. В данный момент под термодинамически равновесным состоянием достаточно понимать состояние, в котором отсутствуют все возможные процессы обмена энергией: 1) ни одна из подсистем системы не совершает работы над другими подсистемами; 2) ни одна из подсистем системы не обменивается теплотой с другими подсистемами системы; 3) ни одна из подсистем системы не обменивается частицами с другими подсистемами системы. Как будет видно в дальнейшем, других видов обмена энергией в обычных (в которых нет процессов рождения и уничтожения частиц) и не существует. Отсюда, в конечном счете, и вытекает достаточность задания всего трех независимых параметров (например: числа частиц, объема и внутренней энергии) для описания термодинамически равновесного состояния однокомпонентной системы.
Если состояние системы меняется со временем, то в системе происходит какой-то процесс. Обратное, вообще говоря, неверно: состояние системы может не меняться, хотя в ней и идет процесс — стационарное, но неравновесное состояние системы. Например, при стационарном процессе переноса тепла состояние системы является неравновесным, хотя и остается неизменным в том смысле, что не меняются распределения температуры, давления, плотности и т. д. по объему системы.
При бесконечно медленном протекании процесса можно считать, что в каждый данный момент времени состояние системы равновесно. Физически это означает, что характерное для процесса время 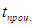 много больше времени установления равновесия в системе
много больше времени установления равновесия в системе 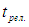 , которое также называют временем релаксации. Такой процесс называют равновесным процессом.
, которое также называют временем релаксации. Такой процесс называют равновесным процессом.
|
Равновесный процесс — это бесконечно медленно протекающий процесс, при котором в каждый данный момент времени состояние системы термодинамически равновесно. |
Очевидно, что равновесный процесс это очередная идеализация. Для того, чтобы процесс можно было считать — с некоторой конечной точностью — равновесным, необходимо чтобы выполнялось неравенство
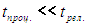
и чем лучше оно выполняется, тем ближе процесс к равновесному.
Равновесный процесс можно представить себе как последовательность равновесных состояний. В дальнейшем будут изучаться (если иное специально не оговорено) лишь равновесные процессы.
Поскольку состояние системы изображается точкой на диаграмме, а процесс — это последовательность равновесных состояний, то такой процесс изображается на диаграмме линией. Каждая точка на линии — условно равновесное промежуточное состояние системы. Равновесный процесс является процессом обратимым, то есть он может протекать в обратном направлении, проходя те же промежуточные состояния в обратном порядке, причем в окружающих телах не останется никаких изменений.
|
Обратимый процесс — это процесс, который может протекать в обратном направлении, проходя те же промежуточные состояния в обратном порядке, причем в окружающих телах не останется никаких изменений. |
Естественно, что в системе тогда не должно действовать никаких сил, подобных силам трения. Ниже мы познакомимся с диаграммами, описывающими некоторые характерные процессы в термодинамических системах.
Зная состояние системы, мы можем найти различные функции состояния — физические характеристики, которые зависят только от состояния системы, то есть они принимают одни и те же значения всякий раз, когда система оказывается в данном состоянии независимо от ее предыстории.
|
Функция состояния — это физическая характеристика, которая зависит только от состояния системы и не зависит от того, как система попала в это состояние. |
Температура. Любая система обладает неким запасом внутренней энергии, не связанной с положением или движением системы как целого относительно внешней среды. О внутренней энергии мы еще поговорим подробнее, а сейчас нам достаточно интуитивного понимания, что, бросив с какой-то скоростью яйцо, мы его не сварим, хотя кинетическая энергия яйца и увеличится. Чтобы приготовить яйцо всмятку, его надо не бросить, а подогреть.
Для количественной характеристики внутренней энергии вводится понятие температуры. Температура занимает особое место в ряду физических величин. Опыт показывает, что она характеризует состояние теплового равновесия тел. Если привести в соприкосновение два тела с разными температурами, то в результате взаимодействия между молекулами эти тела будут обмениваться энергией. Через некоторое время температуры выровняются и передача теплоты прекратится, наступит состояние теплового равновесия. Состояние теплового равновесия и есть то состояние, в которое переходит с течением времени любая изолированная система.
Обычные способы определения температуры основаны на зависимости от нее ряда свойств тел (объема, давления и др.). При этом выбирается термометрическое тело и градуировка температурной шкалы. Наиболее распространенной является стоградусная шкала (шкала Цельсия, рис. 1.3).

Рис. 1.3. Стоградусная шкала Цельсия
Участок этой шкалы между точками замерзания (кристаллизации воды или, что то же самое, плавления льда) и кипения воды при нормальном атмосферном давлении делится на 100 равных частей. Такая часть называется градусом Цельсия (обозначается t °C). Таким образом, точке кристаллизации воды соответствует 0 °С, а точке кипения — 100 °С. Подчеркнем, что и то и другое при нормальном давлении в 760 мм рт. ст. В США используют также шкалу Фаренгейта (обозначается t °F). За нуль своей шкалы Фаренгейт выбрал наинизшую температуру, которую он мог воспроизвести в своей лаборатории — точку плавления смеси соли и льда. Точке замерзания воды в этой шкале соответствует температура 32 °F, а точке кипения — 212 °F. Этот интервал разделен не на сто, а на 180 частей (аналогично угловым градусам). Поэтому градус Фаренгейта меньше градуса Цельсия (фактор 100/180 = 5/9). Связь температур в этих двух шкалах дается формулами
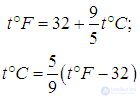
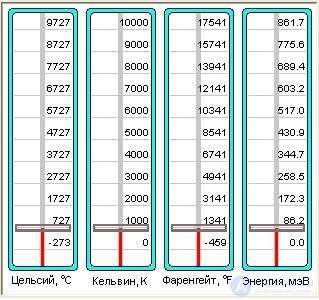
Рис. 1.4. Соответствие между шкалами
В физике пользуются термодинамической (старое название: абсолютной) шкалой температур 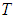 (шкалой Кельвина), которая не зависит от термометрического тела, а устанавливается на основе законов термодинамики.
(шкалой Кельвина), которая не зависит от термометрического тела, а устанавливается на основе законов термодинамики.
В настоящее время один кельвин определяется так: кельвин — единица термодинамической температуры, равная  части термодинамической температуры тройной точки воды. Тройная точка воды была выбрана вместо ее точки кипения потому, что температура тройной точки не зависит от давления и определяется более точно. По шкале Цельсия тройной точке воды соответствует температура
части термодинамической температуры тройной точки воды. Тройная точка воды была выбрана вместо ее точки кипения потому, что температура тройной точки не зависит от давления и определяется более точно. По шкале Цельсия тройной точке воды соответствует температура 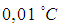 . Величина одного кельвина (обозначается К) совпадает с величиной градуса Цельсия. Учитывая указанное различие в 0,01 кельвина, для связи температур по термодинамической шкале и стоградусной шкале Цельсия, получаем
. Величина одного кельвина (обозначается К) совпадает с величиной градуса Цельсия. Учитывая указанное различие в 0,01 кельвина, для связи температур по термодинамической шкале и стоградусной шкале Цельсия, получаем
|
|
|
(1.1) |
Таким образом, абсолютному нулю температуры 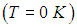 по стоградусной шкале соответствует температура
по стоградусной шкале соответствует температура 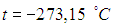 . Как показывает второе начало термодинамики, состояние с температурой равной абсолютному нулю экспериментально недостижимо, так что ноль на шкале Кельвина есть результат экстраполяции.
. Как показывает второе начало термодинамики, состояние с температурой равной абсолютному нулю экспериментально недостижимо, так что ноль на шкале Кельвина есть результат экстраполяции.
Примеры характерных температур в природе показаны на рис. 1.5.

Рис. 1.5. Температура различных физических процессов
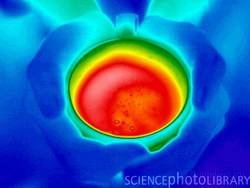
Рис. 1.6. Термограмма чашки горячего чая
В этом разделе мы знакомимся с уравнением состояния идеального газа.
|
идеальный газ — это настолько разреженный газ, что взаимодействием между его молекулами можно пренебречь. |
Эксперименты показали, что при условиях не слишком отличающихся от нормальных (температура порядка сотен кельвинов, давление порядка одной атмосферы) свойства реальных газов близки к свойствам идеального газа.
Пример. На примере водяного пара покажем, что при обычных условиях свойства реальных газов близки к свойствам идеального. По таблице Менделеева можно определить массу моля Н20:
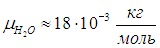
Плотность воды в жидком состоянии
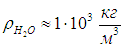
Отсюда можно найти объем одного моля воды:
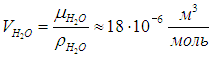
Один моль любого вещества содержит одно и то же число молекул (число Авогадро):
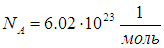
Получаем отсюда объем V1, приходящийся на одну молекулу воды:
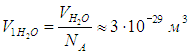
В конденсированном состоянии молекулы располагаются вплотную друг к другу, то есть в сущности V1 есть объем молекулы воды, откуда следует оценка ее линейного размера (диаметра):
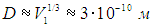
С другой стороны, известно, что объем Vm одного моля любого газа при нормальных условиях равен
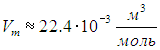
Поэтому на одну молекулу водяного пара приходится объем
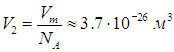
Это значит, что газ можно нарезать мысленно на кубики с длиной ребра
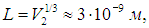
и в каждом таком кубике окажется одна молекула. Иными словами, L — среднее расстояние между молекулами водяного пара. Мы видим, что L на порядок превосходит размер D молекулы. Аналогичные оценки получаются и для других газов, так что с хорошей точностью можно считать, что молекулы не взаимодействуют друг с другом, и при нормальных условиях газ идеален.
Как уже говорилось, уравнение состояния, имеющее вид, позволяет выразить один термодинамический параметр через два других. Конкретный вид этого уравнения зависит от того, какое вещество и в каком агрегатном состоянии рассматривается. Уравнение состояния идеального газа объединяет ряд экспериментально установленных частных газовых законов. Каждый из них описывает поведение газа при условии, что изменяются лишь два параметра.
1. Закон Бойля — Мариотта. Описывает процесс в идеальном газе при постоянной температуре.
|
Изотермический процесс — это термодинамический процесс, протекающий при постоянной температуре. |
Закон Бойля — Мариотта гласит:
|
Для данной массы газа при постоянной температуре Т = const произведение давления газа на занимаемый им объем является постоянной величиной
|
Графически изотермический процесс в различных координатах изображен на рис. 1.7.
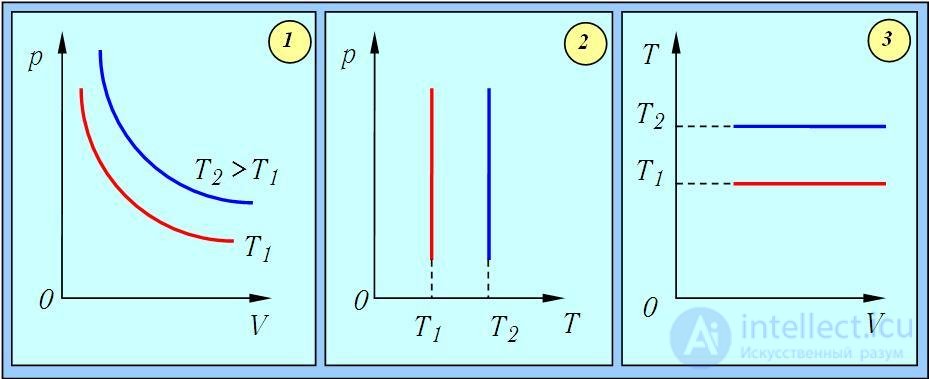
Рис.1.7. Изотермический процесс в идеальном газе: 1 — в координатах p – V; 2 — в координатах p-T; 3 — в координатах T – V
Показанные на рис. 1.7-1 кривые представляют собой гиперболы
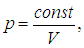
располагающиеся тем выше, чем выше температура газа.
Видео 1.3. Тепловой взрыв: изохорный нагрев газа сопровождается ростом давления.
Экспериментальное исследование закона Бойля — Мариотта можно выполнить с помощью установки, показанной на рис. 1.8. В цилиндре, находящемся при постоянной температуре (что видно из показаний термометра), при перемещении поршня изменяется объем газа. Давление газа измеряется с помощью манометра. Результаты измерений давления и объема газа представляются на диаграмме p = p(V).
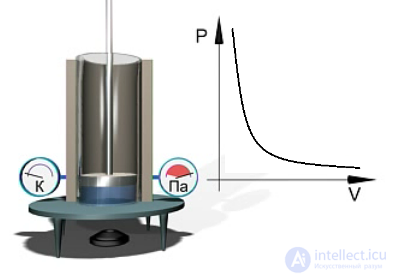
Рис. 1.8. Экспериментальное изучение изотермического процесса в газе
2. Закон Гей-Люссака. Об этом говорит сайт https://intellect.icu . Описывает тепловое расширение идеального газа при постоянном давлении.
продолжение следует...
Часть 1 1. Идеальный газ
Часть 2 1.3. Кинетическая теория идеальных газов - 1. Идеальный газ
Часть 3 1.5. Смеси газов - 1. Идеальный газ
Часть 4 - 1. Идеальный газ
Комментарии
Оставить комментарий
Молекулярная физика и термодинамика
Термины: Молекулярная физика и термодинамика