Это продолжение увлекательной статьи про идеальный газ.

...

style="width:567px">

Изобарный процесс — это процесс, протекающий при постоянном давлении.

Закон Гей-Люссака гласит:

Объем данной массы определенного газа при постоянном давлении пропорционален его абсолютной температуре (1.3)

Графически изобарный процесс в различных координатах показан на рис. 1.9.

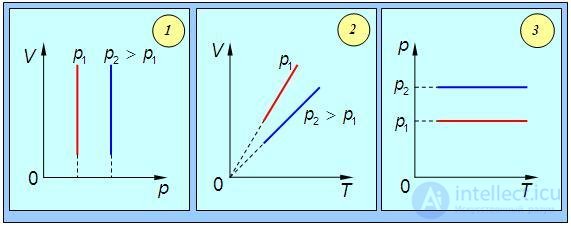
Рис. 1.9. Изобарный процесс в газе: 1 — в координатах p – V; 2 — в координатах V – T; 3 — в координатах P – T

Экспериментальное изучение закона Гей-Люссака можно выполнить с помощью установки, показанной на рис. 1.10. В цилиндре газ нагревается с помощью горелки. Давление газа в процессе нагревания остается неизменным, что видно из показаний манометра. Температура газа измеряется с помощью термометра. Результаты измерений давления и температуры газа представляются на диаграмме V = V(Т).

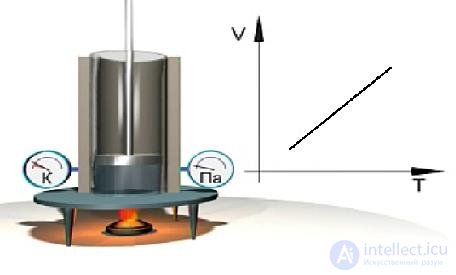
Рис. 1.10. Экспериментальное изучение изобарного процесса в газе

3. Закон Шарля. Описывает изменение давления идеального газа с ростом температуры при постоянном объеме.

Изохорный процесс — это процесс, протекающий при постоянном объеме.

Закон Шарля гласит:

Давление данной массы определенного газа при постоянном объеме пропорционально термодинамической температуре (1.4)

Графически изохорный процесс в различных координатах показан на рис. 1.11.

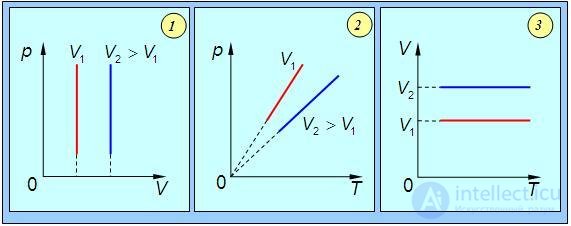
Рис.1.11. Изохорный процесс в газе: 1 — в координатах p – V; 2 — в координатах p – T; 3 — в координатах V – T

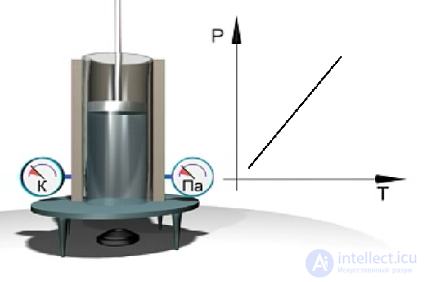
Экспериментальное исследование закона Шарля можно выполнить с помощью установки, показанной на рис. 1.12. В цилиндре газ занимает постоянный объем (поршень неподвижен). При нагревании давление газа увеличивается, а при охлаждении уменьшается. Величина давления измеряется с помощью манометра, а температура газа — с помощью термометра. Результаты измерений давления и температуры газа представляются на диаграмме p=p(Т).

Рис. 1.12. Экспериментальное изучение изохорного процесса в газе

Если объединить рассмотренные частные газовые законы, то получим уравнение состояния идеального газа (для одного моля)

(1.5)

в которое входит универсальная газовая постоянная R = 8,31 Дж/(моль· К). При одних и тех же значениях объема и температуры системы давление газа пропорционально числу молей вещества

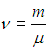
Поэтому для произвольной массы газа m уравнение состояния идеального газа (1.6) примет вид

(1.6)

Это уравнение называют уравнением Клапейрона — Менделеева.

1.3. Кинетическая теория идеальных газов

В этом разделе мы переходим к молекулярно-кинетическому описанию идеального газа.

При выводе основного уравнения молекулярно-кинетической теории газов будем считать молекулы маленькими твердыми шариками, в среднем абсолютно упруго и зеркально отражающимися от стенок сосуда. Силы взаимодействия возникают только при соударении молекул друг с другом или со стенками сосуда. Припишем каждой молекуле номер i (i = 1, 2, ..., N), где N — полное число молекул в системе.

Прежде чем приступить непосредственно к расчету, поясним, почему в среднем столкновения молекул со стенкой мы не только можем, но — в условиях термодинамического равновесия — обязаны считать абсолютно упругими и зеркальными. «Абсолютно упругими», то есть в среднем скорость молекулы после столкновения со стенкой равна ее скорости до столкновения со стенкой. «Зеркальными» означает, что угол отражения молекулы от стенки равен углу падения молекулы на стенку (углы падения и отражения определяются как в оптике: это углы между направлением нормали к стенке и вектором скорости молекулы). Это легко доказывается «от противного». Ранее равновесное состояние было определено, в частности, как такое, в котором отсутствуют потоки энергии, импульса, момента импульса и т. д. Следовательно, если газ и стенка сосуда находятся в термодинамическом равновесии друг с другом, то не должно быть потока энергии из газа в стенку или из стенки в газ. Легко видеть, что если молекула газа в среднем отскакивает от стенки с меньшей (большей), чем подлетала, скоростью, то стенка получает от газа (отдает газу) энергию, что при равновесии невозможно. Противоречие не возникает только в том случае, когда в среднем эти скорости равны, то есть в среднем столкновение абсолютно упругое (рис. 1.13).

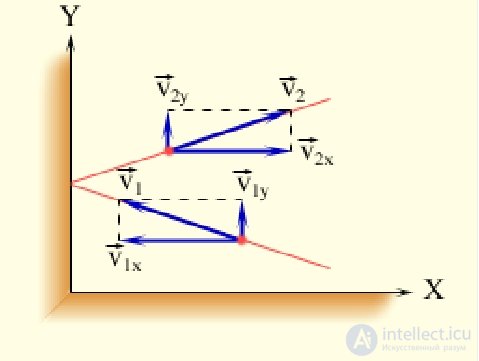
Рис. 1.13. Абсолютно упругое столкновение молекулы со стенкой»

Подчеркнем, что обмен энергией между газом и сосудом не противоречит закону сохранения энергии: сколько получил газ, столько отдала стенка и наоборот. Как будет видно в дальнейшем, такой обмен энергией противоречит второму началу термодинамики. Аналогично доказывается равенство углов падения и отражения. Если они не равны, то между сосудом и газом будет происходить обмен моментом импульса. Проще можно сказать так: произойдет самораскручивание газа в одну сторону, а сосуда — с равным по модулю моментом импульса — в другую, что также вовсе не запрещено законом сохранения момента импульса, но противоречит второму началу термодинамики. Поскольку второе начало термодинамики в данный момент еще не сформулировано, отметим, что в эксперименте таких процессов никто никогда не видел, а поскольку экспериментальных причин сомневаться в справедливости второго начала термодинамики нет, то и не увидит.

Выше мы все время подчеркивали: в среднем. Это связано с тем, что «судьба» конкретной индивидуальной молекулы при ее столкновении со стенкой сосуда может быть какой угодно. Чтобы это понять надо «спуститься» с макроскопического на микроскопический уровень рассмотрения процесса столкновения молекулы газа со «стенкой». Произнося слово «стенка», мы имеем ввиду границу раздела между газом (разреженное состояние вещества, концентрация частиц ~10¹⁹ в см³) и стенкой (плотное — конденсированное состояние вещества, концентрация частиц ~10²² в см³).

Видео 1.5. Поведение броуновской частицы доказывает, что соударения молекул со стенкой абсолютно упруги и зеркальны лишь в среднем

Претендуя лишь на сугубо качественное описание далеко не всех процессов имеющих место при взаимодействии молекулы газа с твердой или жидкой поверхностью, рассмотрим лишь два возможных случая.

Пусть, к примеру, сосуд железный, тогда около положений равновесия (узлов кристаллической решетки) колеблются ионы железа. Пусть в сосуде воздух, будем следить за некоторой молекулой азота, подлетающей к «стенке». Она столкнется не со стенкой «вообще», а с конкретным ионом железа в составе стенки, на определенной стадии его колебаний. Скорость молекулы относительно стенки это ее скорость относительно узлов кристаллической решетки — положений равновесия ионов железа. Если в момент столкновения тот конкретный ион, с которым сталкивается наша молекула, двигался ей навстречу, то, относительная скорость молекулы и иона будет больше, чем молекулы и стенки. Позволим себе такой язык: «наподдаст» он ей и отлетит она от стенки со скоростью большей, чем подлетала. И наоборот, если в момент столкновения тот конкретный ион, с которым сталкивается наша молекула, двигался от нее, то, относительная скорость молекулы и иона будет меньше, чем молекулы и стенки. В этом случае молекула отлетит от стенки со скоростью меньшей, чем подлетала. Очевидно, что в состоянии термодинамического равновесия столкновения, сопровождающиеся увеличением и уменьшением скорости отлетающих от стенки молекул, должны происходить — в среднем за достаточно большое время — одинаково часто.

Наконец, подлетающая к стенке молекула может попасть в «междуузелье» — пространство между соседними узлами кристаллической решетки, внедриться в кристаллическую решетку и застрять в нее так прочно, что только достаточно сильный нагрев стенки будет способен «выгнать» ее оттуда. Например, на установках типа «Токамак» предназначенных для исследований высокотемпературной плазмы, предусматривают нагрев стенок для их «обезгаживания» — освобождения от налипших на стенки молекул воздуха.

Теперь рассмотрим молекулу с номером i, которая подлетает к стенке сосуда, перпендикулярной оси ОХ, со скоростью 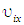и импульсом 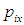. При абсолютно упругом и зеркальном отражении молекулы от стенки знак проекции ее ее импульса на ось ОХ меняется на противоположный 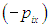, так что приращение проекции импульса молекулы на ось ОХ равно

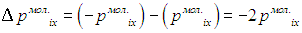
а приращение импульса стенки, другими словами, импульс переданный стенке, равен

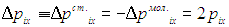
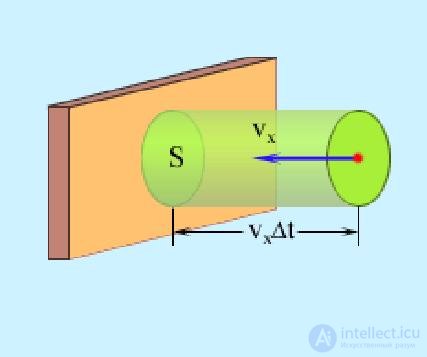
Рис. 1.14. Отражение молекулы от стенки

Предполагая, что между собой молекулы не сталкиваются, можно утверждать, что молекула после отражения долетит до противоположной стенки, снова отразится и в следующий раз подлетит к той же стенке (рис. 1.14) через время

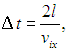
где 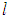— расстояние между стенками, перпендикулярными оси x. Поскольку импульс 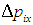передается стенке каждые 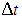секунд, на стенку со стороны одной молекулы действует средняя сила

(Заметим на будущее, что средние значения величин мы будем обозначать угловыми скобками).

Если в сосуде заключено N молекул, то полная средняя сила F получится суммированием выражения (1.8) по всем молекулам:

При этом, так как все направления равноправны и молекулы в среднем совершенно одинаково отражаются от всех стенок сосуда, то, во-первых, сумма произведений импульсов на скорости представима в виде

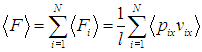
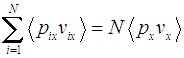
где справа написано одинаковое для всех молекул среднее. И, во-вторых:

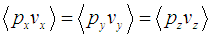
С другой стороны, среднее значение произведения импульса молекулы на ее скорость определяется как

Поэтому

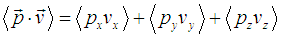
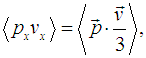
и выражение для полной средней силы, действующей на стенку со стороны газа, приобретает вид

Разделив полную среднюю силу на площадь стенки 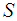, мы, по определению давления, получим выражение для давления газа 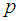на стенку. Заменяя произведение 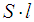на объем сосуда 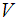, приходим к уравнению

Используем теперь тот факт, что скорость движения молекул даже при температурах в тысячи кельвинов, когда большинство веществ уже переходит в плазменное состояние, составляет всего несколько километров в секунду, то есть о релятивистских эффектах в атомарных и молекулярных газах говорить не приходится, поэтому импульс молекулы 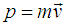, где 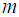— масса молекулы. Тогда из (1.9) следуют два соотношения (по сути это одно соотношение), каждое из которых называют основным уравнением молекулярно-кинетической теории газов:

или

Здесь 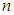— концентрация молекул, <Е_ПОСТ> — средняя кинетическая энергия поступательного движения, приходящаяся на одну молекулу. Произведение N<Е_ПОСТ> есть полная кинетическая энергия поступательного движения всех молекул газа в данном объеме V.

Быть может, на первый взгляд трудно узнать в соотношениях (1.10–1.11) сходство со знакомым нам уравнением Клапейрона — Менделеева

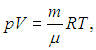
поэтому слегка преобразуем последнее. Введем новую величину — постоянную Больцмана

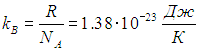
Важность этой физической постоянной определяется тем, что с ее помощью устанавливается связь между энергией и температурой, как это видно уже из ее размерности. Далее используем, что

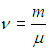
— число молей вещества в системе, а N_A — число молекул в одном моле, так что nN_A равно полному числу частиц в системе. Приходим тогда к следующей форме уравнения Клапейрона — Менделеева:

Сравнивая (1.10) с (1.12), мы видим, что, в сущности, имеем дело с аналогичным уравнением, если определить абсолютную температуру соотношением

Такое определение температуры годится только для систем, состоящих из частиц только с тремя поступательными степенями свободы, во-первых, и если поступательное движение этих частиц точно описывается законами классической, в данном случае «классической» означает — не квантовой механики. Например, оно не применимо для описания колебательного движения ядер в молекулах кислорода и азота (основные компоненты воздуха) при комнатных температурах, не применимо для описания поступательного движения электронов в металлах при любых температурах потому, что и то и другое движения носят квантовый характер и законами классической механики не описываются.

Общее, годное на все случаи жизни, определение температуры будет дано позже на базе первого и второго начал термодинамики, а сейчас отметим следующее.

Температура есть мера интенсивности теплового движения. Температура растет с ростом средней энергии теплового движения. Как будет видно в дальнейшем, этот рост вовсе не обязательно должен быть пропорциональным ростом, как в соотношении (1.13).

Видео 1.6. Классическая модель газа с растущей температурой.

Пример. В подземной полости радиусом 100 м проводится подземное испытание ядерного оружия мощностью 50 килотонн. Оценим давление газа в полости и минимальную глубину испытательной шахты, чтобы продукты взрыва не вырвались наружу.

Для решения задачи в приведенной формулировке нам пока не хватает данных. Сначала надо найти полную энергию газа, образовавшегося при взрыве. Намек на ее величину содержится в указании так называемого тротилового эквивалента. По традиции энергию взрыва сравнивают с энергией взрыва тротила. Энергия W взрыва 50-килотонной бомбы эквивалентна энергии взрыва 5⋅10⁴ т = 5⋅10⁷ кг тротила. В справочнике находим, что энергия взрыва 1 кг тротила равна 4,2 МДж. Таким образом, при взрыве этой бомбы выделяется энергия

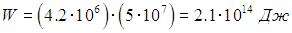
Поскольку взрыв происходит в полости, будем считать, что вся эта энергия превратилась в кинетическую энергию продуктов взрыва. Так как нам известен объем полости

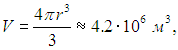
то величину давления находим из основного уравнения молекулярно-кинетической теории газов (1.12)

Получим теперь ответ на второй вопрос задачи. Газы не вырвутся наружу, если внешнее давление породы над полостью превышает давление продуктов взрыва. Внешнее давление можно оценить по известной формуле гидростатики

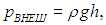
где ρ — плотность породы. Подчеркнем, что эта формула справедлива для газов и жидкостей. Применительно к твердому телу ее можно использовать как оценочную. В справочнике находим, например, плотность гранита ρ = 2600 кг/м³, которую можно взять за основу оценки. Из равенства

находим минимальную глубину шахты h:

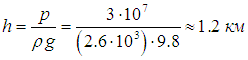
В заключение этого раздела сделаем замечание. Мы специально не предполагали с самого начала классической зависимости импульса частицы от ее скорости. Поэтому уравнение (1.9) имеет более широкую область применимости, нежели (1.10). Например, электромагнитное излучение можно представить как совокупность особых частиц (фотонов), движущихся со скоростью света. Поэтому для фотонов

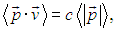
где с — скорость света. С другой стороны, энергия фотонов Е_g связана с их импульсом соотношением

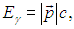
так что уравнение (1.9) приобретает в этом случае вид

Мы видим, что уравнение состояния идеального газа фотонов отличается числовым множителем в правой части от соответствующего уравнения для газа обычных частиц.

1.4. Распределение энергии по степеням свободы молекулы

Чтобы разобраться в связи температуры с внутренней энергией, повторим введенное ранее в механике понятие — число степеней свободы.

В § 1.3 было показано, что давление газа численно равно импульсу, который передается за единицу времени единице площади стенки в результате ударов по ней молекул, поэтому давление определяется средней энергией только поступательного движения молекул.

Поступательное движение любой системы «как целого» полностью определяется движением одной единственной точки: ее центра масс. В частности, полный импульс любой нерелятивистской системы, равен произведению массы 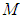этой системы на скорость 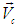движения ее центра масс. Энергия поступательного движения системы «как целого» равна 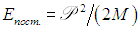. Поэтому, для полного описания поступательного движения любой системы в трехмерном пространстве необходимо и достаточно задание значений трех координат центра масс. Таким образом, поступательному движению, как бы ни была устроена система, всегда соответствуют три поступательных степени свободы: .

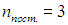Можно сказать и так: «с точки зрения поступательного движения» любая система может быть точно, а не приближенно, представлена в виде одной единственной материальной точки совпадающей с центром масс системы и имеющей массу равную массе системы (рис. 1.15).

Рис. 1.15. Одноатомная молекула

Если же говорить о полной внутренней энергии газа U, то она складывается, вообще говоря, из многих компонентов, соответствующих всем возможным видам движения в молекуле и энергии взаимодействия молекул между собой. При рассмотрении идеального газа, энергией взаимодействия молекул пренебрегают.

Рассмотрим для начала благородный газ, например, гелий 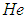. Дело в том, что все благородные газы одноатомны, из них гелий самый легкий и, соответственно, самого простого устройства. Атом гелия (имеется в виду основной изотоп 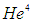) — это положительно заряженное ядро из 2 протонов и 2 нейтронов и электронная оболочка из 2 отрицательно заряженных электронов. Итого 6 частиц, если каждую из них считать материальной точкой, то это 18 степеней свободы. Но, не все так удручающе мрачно, выручает квантовая механика. Не вдаваясь в «квантовые» подробности, укажем, что для изменения состояния электронной оболочки атома гелия, а именно: для перевода ее из основного состояния с минимально возможной энергией в имеющее большую энергию возбужденное состояние необходима минимальная энергия около 20 эВ. Более точно, например, при возбуждении электронной оболочки атома гелия возможен переход, требующий 19,8198 эВ. Энергетический спектр атомов дискретен: принять меньшую энергию атом гелия просто не может, он так устроен. При столкновении атома гелия с электроном меньшей энергии, атом гелия останется в исходном — основном состоянии с наименьшей возможной внутренней энергией, величина которой зависит только от выбора начала отсчета энергии, и, чаще всего, принимается просто равной нулю. Такое столкновение будет абсолютно упругим. Отметим, что

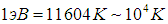
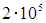Поэтому энергии в 20 эВ соответствует температура порядка кельвинов. Наверное нетрудно сообразить, что даже при температуре в 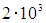К атомов гелия движущихся столь быстро, что энергия их относительного движения в 100 раз больше ее среднего значения, будет ничтожно мало. Но, тогда столкновения, сопровождающиеся изменением внутренней энергии одного из сталкивающихся атомов, будут чрезвычайно редки, следовательно, возможным наличием атомов с возбужденной электронной оболочкой можно пренебречь и приближенно считать, что все атомы имеют электронную оболочку в одном и том же основном состоянии с минимально возможной энергией. Не так важно, что электронные оболочки всех атомов имеют минимально возможную энергию, как важно, что она одна и та же у всех атомов и не меняется даже при сильном нагреве газа. Тогда, суммарная энергия электронных оболочек всех атомов есть просто константа равна 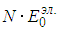, где N — число атомов в газе, а 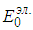— энергия электронной оболочки каждого из атомов. При фиксированном полном числе атомов эта величина ни от каких параметров состояния газа не зависит. Остается еще раз вспомнить, что энергия всегда определена с точностью до аддитивной постоянной и выбросить эту константу, изменив начало отсчета энергии.

Для изменения состояния ядер атомов необходима энергия в сотни тысяч эВ, что «по газовым масштабам» чудовищно много. Соответствующие температуры наблюдаются лишь во внутренних областях Звезд. Поэтому о возможности изменения внутреннего состояния ядер в процессе столкновений в газе говорить не приходится (имеются ввиду стабильные ядра, возможный распад нестабильных ядер не имеет отношения к параметрам состояния газа).

Что же остается? Остается поступательное движение атома как целого, то есть три поступательных степени свободы. Это оправдывает использование такой модели:

На всякий случай оговоримся, что в данный момент нас не интересуют процессы установления в газе термодинамического равновесия. Равновесие устанавливается именно в результате взаимодействия частиц газа при их столкновениях, поэтому модель «атом — материальная точка» такие процессы не описывает.

Положение с электронной оболочкой не меняется, если атомы входят в состав многоатомной молекулы. Минимальная энергия, необходимая для изменения состояния (возбуждения) электронной оболочки молекул примерно та же, что и для возбуждения электронных оболочек атомов. Характерная для атомно-молекулярного мира цифра составляет порядка 10 эВ, чему соответствует температура порядка сотни тысяч кельвинов. При таких температурах газ уже не газ, а низкотемпературная плазма. Поэтому, пока газ остается газом, в подавляющем большинстве случаев, можно с великолепной точностью считать, что электронные оболочки всех молекул газа находятся в одном и том же состоянии, их суммарная энергия есть не зависящая от параметров состояния газа константа, которую можно опустить. Конечно

продолжение следует...

Продолжение:

Часть 1 1. Идеальный газ
Часть 2 1.3. Кинетическая теория идеальных газов - 1. Идеальный газ
Часть 3 1.5. Смеси газов - 1. Идеальный газ
Часть 4 - 1. Идеальный газ