Экспрессия генов, генетические операторы фитнес функция в генетических алгоритмах

Сразу хочу сказать, что здесь никакой воды про экспрессия генов, и только нужная информация. Для того чтобы лучше понимать что такое экспрессия генов, генетические операторы , настоятельно рекомендую прочитать все из категории Эволюционные алгоритмы.

Введение.

Эволюционные алгоритмы (ЭА) представляют собой направление в искусственном интеллекте, использующем и моделирующем биологическую эволюцию. Среди ЭА – стохастических и включающих в себя эволюционное программирование, эволюционные стратегии, генетические алгоритмы, генетическое программирование, в частности, программирование с экспрессией генов, наиболее распространены генетические алгоритмы (ГА). ГА – это метод машинного обучения, основанный на механизмах отбора в природе, которые ведут случайный и параллельный поиск решений, оптимизирующих заранее определенную фитнес-функцию. Генетическое программирование (ГП) создано в качестве самостоятельного направления в области эволюционных вычислений, несмотря на то, что этот метод может быть также интерпретирован как особый класс ГА. В ГП адаптированы и применены аналогичным ГА образом основные механизмы отбора, рекомбинации и мутации. Более общее представление проблем в ГП позволяет определить особь популяции как структуру, формулу или даже в более общем случае как программу. Это позволяет рассматривать новые области применения ЭА. Различие между ГА и ГП выражено не сильно: обе системы используют один вид объектов, который служит как генотипом, так и фенотипом. Такой подход имеет одно из двух ограничений: простота применения генетических операторов к объектам означает их недостаточную выразительность и сложность этих объектов (в случае ГА), а их сложность ведет к трудностям при воспроизводстве и модификации (в случае ГП). Программирование с экспрессией генов (ПЭГ) реализуется с помощью алгоритма :

1. Создание начальной популяции

2. Декодирование особей

3. Выполнение программ особей

4. Вычисление фитнес-функции (ФФ) особей

5. Проверка критерия останова алгоритма (достигнута требуемая точность либо истекло лимитированное время выполнения)

6. Копирование лучшей особи (элитизм)

7. Отбор

8. Репликация

9. Мутация

10. Операторы переноса

11. Операторы рекомбинации

12. Возврат к п. 2

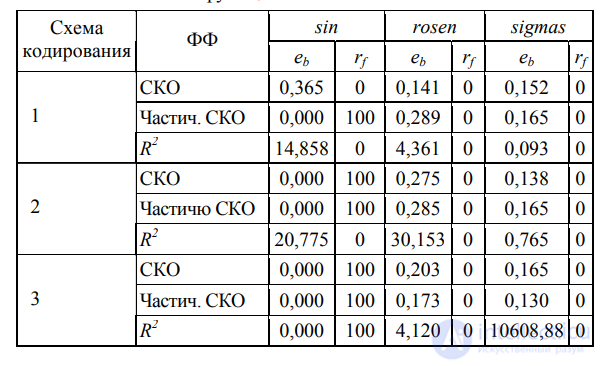
В ПЭГ применяются следующие операторы: репликации, мутации, копирования со сдвигом, копирования со сдвигом в корень, перестановки генов, однои двухточечной рекомбинации, генной рекомбинации. Репликация представляет собой самый простой оператор, не вносящий разнообразие в геном, и используется в паре с оператором отбора для копирования особей в новую популяцию в соответствии со значением ФФ и случайностью, вводимой оператором рулетки. Мутация (замена символа – элемента гена, соответствующего узлу дерева) может возникнуть в любом месте хромосомы. Вероятность оператора, как правило, задается эквивалентной двум мутациям в хромосоме. Элементы, подверженные мутации в голове гена, могут быть изменены на любой другой символ (функцию или терминал), в хвосте – только на терминал. Данное ограничение должно гарантировать сохранение структуры хромосомы и обеспечение декодирования синтаксически правильного дерева. Среди всех модифицирующих операторов мутация наиболее существенный и эффективный, так как в отличие от остальных, комбинирующих существующие участки генома, мутация направлена на создание новых элементов, а потому вносит наиболее радикальные изменения, расширяя область поиска решений. Рекомбинация – операция по перемещению последовательных участков генома в пределах хромосомы. Цель данной статьи – исследование влияния выбора генетических операторов на свойства алгоритма ПЭГ. В статье описана методика оценки эффективности модификаций алгоритма ПЭГ, заключающаяся в статистической обработке результатов множества запусков с целью получения среднеквадратичной ошибки (CKO) наилучшей модели среди всех запусков (еb) и доли успешных запусков (rf), т.е. таких, в ходе которых была получена модель с приемлемой для данной задачи точностью. Для тестирования использованы модели синусоиды (sin), функция Розенброка (rosen) и сумма четырех сигмоид (sigmas). Эти же методика и модели использованы в данной работе для сравнения генетических операторов.

Операторы отбора

Процесс эволюции основан на генетической изменчивости и процедуре отбора. Данные механизмы задействованы во всех эволюционных алгоритмах. Однако способ обеспечения генетической изменчивости, который можно было бы назвать лучшим, не был выявлен. Исследователи разделяют эти способы на мутацию и рекомбинацию. Успешность эволюции также существенно зависит от применяемых алгоритмом генетических операторов, размера и состава начальной популяции.

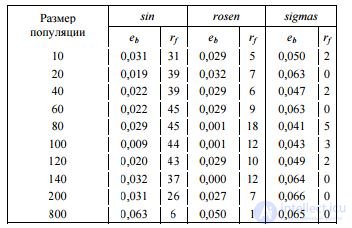
Сравнивая эффективность стандартного (традиционного) алгоритма ПЭГ при разных размерах популяции, следует учесть, что время выполнения алгоритма прямо пропорционально размеру популяции. Поэтому для оценки данного фактора в условиях ограниченного времени каждому запуску было отведено фиксированное время работы, чтобы алгоритмы с большим размером популяции имели возможность рассчитать меньшее число поколений. Результаты эксперимента для различного количества особей, приведенные в табл. 1, свидетельствуют о наличии пика эффективности при размере популяции 80–120 особей

Таблица 1. Эффективность алгоритма при различных размерах популяции

Одно из важнейших применений ПЭГ – символьная регрессия, цель которой – поиск выражения, наиболее соответствующего известным заданным значениям с определенной погрешностью. Установка небольшого значения (абсолютного или относительного) допустимой погрешности позволяет обнаружить хорошие решения некоторых математических задач, однако в большинстве случаев задание малой погрешности замедляет процесс эволюции вследствие более строгого отбора особей. Если же задать слишком большую допустимую погрешность, отбору подвергнется множество особей, не являющихся приемлемыми решениями, однако значение ФФ которых будет очень высоким. Отбор особей в ПЭГ осуществляется пропорциональным оператором рулетки с простым элитизмом: лучшая особь популяции переносится в следующее поколение, шансы остальных прямо пропорциональны значениям их ФФ. Такая форма элитизма гарантирует сохранение лучшего обнаруженного решения. Каждый запуск рулетки выбирает одну особь, соответственно, количество запусков рулетки равно размеру популяции. После отбора новой популяции поочередно выполняются генетические операторы , применяемые к случайным образом выбранным особям. Например, если вероятность оператора составляет 70 процентов, то семь из 10 особей будут им модифицированы. Каждая особь может быть модифицирована сразу несколькими операторами, каждый из которых может быть применен к особи лишь однократно. Это отличает ПЭГ от генетического программирования (ГП), в котором особь не изменяется более чем одним оператором за итерацию. Получаемое таким образом потомство существенно отличается от родительских особей. Наиболее универсальным оператором отбора с достаточной эффективностью, применяемым в ПЭГ, будет алгоритм рулетки, в котором вероятность дальнейшего участия особи в процессе эволюции напрямую определяется значением ее ФФ, что ведет к сохранению особей только с высоким значением ФФ. Однако если значение ФФ одной из особей популяции в определенный момент значительно превышает значение ФФ остальных, это приводит к застреванию алгоритма в локальном оптимуме и потере множества особей с тенденцией к улучшению с небольшими текущими значениями ФФ. В работе предложена формула отбора, заимствованная из иммунных алгоритмов и основанная на понятии плотности D особи

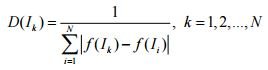
и высказано предположение о том, что данная формула отбора гарантирует разнообразие генетического материала в популяции. Здесь N – количество особей в популяции; f – фитнес-функция. Значения плотности используются затем для вычисления вероятности отбора

Таким образом, чем больше особей похожи (по критерию вероятности) на особь k I , тем меньшую вероятность отбора она имеет. Однако авторами не отмечается тот факт, что при данном подходе особи с принципиально разными синтаксическими деревьями, но равными значениями ФФ будут неотличимы друг от друга. Сравнение различных подходов к механизму отбора представлено в табл. 2. В данной и в по-

Таблица 2. Эффективность алгоритма с различными операторами отбора и размерами популяции

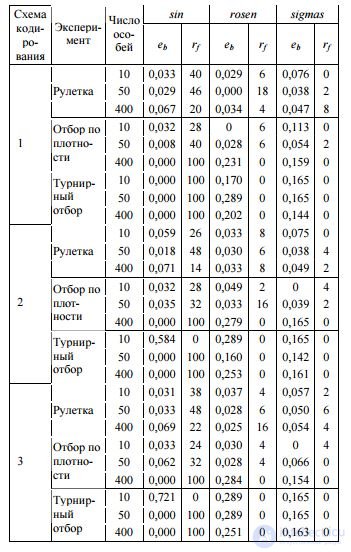
следующих таблицах в колонке «Схема кодирования» цифра 1 соответствует традиционному кодированию, 2 – префиксному, 3 – кодированию с наложением. Во всех случаях реализация простого элитизма осуществлялась путем сохранения лучшей особи. Анализ этих результатов позволяет сделать определенные выводы. Во-первых, целесообразно использование популяции в 50 особей: это экспериментально полученное оптимальное значение характерно для всех девяти проведенных экспериментов. Вовторых, традиционный алгоритм ПЭГ (с кодированием путем обхода графа в ширину) достигает максимума своей производительности при использовании турнирного отбора. В-третьих, для ПЭГ с наложением оптимален отбор по плотности. В-четвертых, наилучшие результаты показывает применение префиксного ПЭГ в комбинации с оператором рулетки. Итак, рассматривая операторы отбора вне зависимости от способа кодирования, можно сделать вывод о том, что оптимальным будет выбор оператора рулетки, как и было предложено автором традиционного алгоритма ПЭГ .

Оператор мутации

Влияние на динамику эволюции. Об этом говорит сайт https://intellect.icu . В системах на основе генотипа и фенотипа пространство поиска отделено от пространства решений, что существенно улучшает производительность таких систем. Чем меньше ограничений накладывается на процедуру проецирования генотипа на фенотип и обратно, тем более эффективна система, так как практически любой оператор, включая мутацию, может быть использован для исследования пространства поиска. Так, например, в системе DGP (Developmental Genetic Programming – ГП с развитием ) в результате трансляции генотипа в фенотип не всегда получается синтаксически правильное дерево, что приводит к дополнительным операциям по удалению непригодных особей. Поэтому мутация в DGP не превосходит по показателям операторы кроссовера. В работе для сравнения эффективности генетических операторов, применяемых в ПЭГ, были сопоставлены динамические данные процесса эволюции: графики значений ФФ лучшей особи с течением поколений (итераций) и графики средних значений ФФ популяции.

В ходе поиска модели, созданной формулой y(x) = x 4 + x 3 + x 2 + x , исследована динамика эволюционного процесса с различными значениями вероятности применения оператора мутации (pm1, pm2, pm3, pm4). Полученные значения ФФ приведены на рис. 1. а б в г

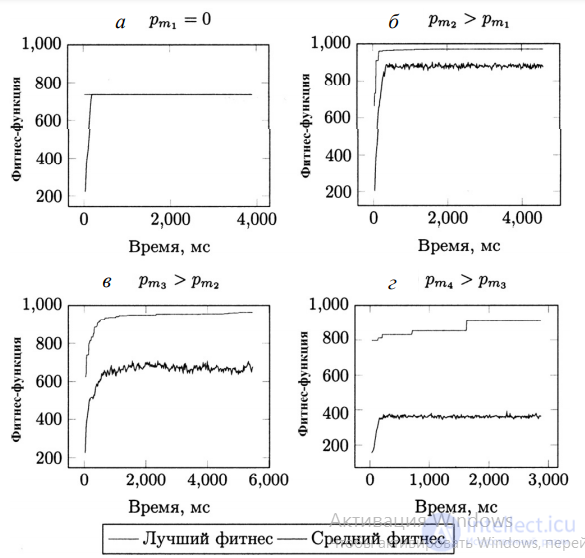
Рис. 1. Динамика эволюции при разных вероятностях мутации

На рис. 1,а видно, что график лучших значений ФФ практически совпадает с графиком средних значений ФФ, особенно в поздних поколениях. Такие популяции называются умеренно инновационными в силу небольшого различия между особями и медленного процесса эволюции. Вероятность успешного обнаружения решения задачи (отношение запусков, в ходе которых решение было обнаружено, к общему количеству запусков алгоритма), поставленной в эксперименте, составила 16 процентов. На рис. 1,б заметно, что форма графиков совпадает (без учета колебания графика средних значений ФФ), однако они не пересекаются, между ними наблюдается разрыв. Процентное соотношение успешных запусков составило 47 процентов. Такая модель эволюции – здоровая, но слабая. С повышением вероятности мутации возрастает успешность алгоритма, достигая максимума при pm3 = 0,1, показанного на рис. 1,в и соответствующего здоровой и сильной модели.

Для этого случая характерен больший разрыв между графиками, однако тенденция к росту среднего значения ФФ сохраняется. Наконец, последняя приведенная динамика со средним значением ФФ на постоянном низком уровне с небольшими колебаниями служит примером полностью хаотической системы, в которой, несмотря на элитизм, каждое поколение – по сути случайное. Исследование операторов рекомбинации в качестве единственных источников, вносящих генетическое разнообразие, выявило процесс усреднения популяции – быстрое сокращение разрыва между графиками лучшего и среднего значений ФФ с последующим их перекрытием. Это означает, что геном всех особей популяции совпадает, и разнообразие устранено, что есть следствием преждевременной сходимости такого подхода к локальному оптимуму. В начальной популяции, заполненной особями, созданными случайным образом, жизнеспособные решения – событие редкое, особенно при решении сложных задач. Удачным подходом в таком случае является начало процесса эволюции с одной или несколькими особями–основателями . Эффект основателя, описанный Э. Майром, как создание новой популяции из особей–основателей, может быть инициирован дрейфом генов – изменением частоты вариантов генов вследствие случайных процессов и работы операторов отбора. Пример наиболее выраженного случая эффекта основателя – колонизация необитаемой области (создание новой популяции) одной особью. Это означает, что при определенном значении вероятности мутации можно добиться максимальной эффективности работы всего алгоритма. Кроме того, оператор мутации уменьшает тенденцию популяции к гомогенизации (утрате разнообразия) и устраняет сильную зависимость эффективности алгоритма от размера популяции. Влияние на производительность. Влияние наиболее вероятных значений среднего количества мутаций в хромосоме на работу алгоритмов с различными способами кодирования синтаксических деревьев показано в табл. 3.

Модификации

Наиболее существенным недостатком алгоритма ПЭГ есть его склонность к преждевременной сходимости к локальному оптимуму, потому любые техники, направленные на решение этой проблемы, приводят к существенному росту производительности ПЭГ, что выражается в сокращении времени сходимости, улучшении средней приспособленности решений и повышению вероятности успешного обнаружения оптимального решения. Для усиления способности алгоритма к поиску в предложен следующий алгоритм динамической мутации DM–GEP. При максимальном количестве поколений Т процесс эволюции разбивается на три фазы:  Начальная фаза: поколения от первого до T1,0 < T1 < T. Вероятность мутации pm возрастает каждые два поколения со значения 0,022 до 0,44 с шагом 0,001.

 Метафаза: поколения от T1 до T2,T1 Вероятность мутации pm возрастает каждые пять поколений от значения 0,022 до 0,66 с
шагом 0,002.
 Анафаза: поколения от T2 до Т. Вероятность мутации pm уменьшается каждые десять поколений от значения 0,066 до 0,022 с шагом 0,001.

В работе предложено использовать динамическую установку вероятности мутации
как самого разрушительного оператора, делая
ее индивидуальной для каждой особи и зависимой от ФФ особи. Чем выше ФФ особи, тем
более она приспособлена, тем больше внимания требуется уделять локальному поиску, тем
меньшая вероятность мутации устанавливается.

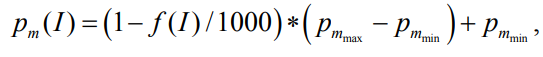
где 1000 – максимальное значение фитнеса;
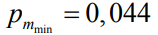и 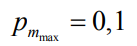– нижний и верхний
пределы вероятности мутаций соответственно.
Производительность ПЭГ существенно зависит от заданных вероятностей применения ге-
нетических операторов. Снизить влияние этих
значений на работу алгоритма можно с помощью подхода выбора нового значения, приня-
того в методе симуляции отжига , суть которого состоит в использовании зависящего от
времени (номера итерации алгоритма) параметра Т, называемого температурой. Чем выше
температура в данный момент времени, тем
более вероятна замена исходной особи новой,
полученной путем применения генетического
оператора. Температура системы уменьшается
с каждой последующей итерацией, способствуя поиску окрестностей глобального оптимума на первой фазе алгоритма и приводя затем к
уточнению его местоположения. Скорость понижения температуры управляется некоторым
параметром а.
При таком подходе на каждой итерации алгоритма ПЭГ ко всем родительским особям old
последовательно применяются генетические
операторы, каждый из которых порождает новую дочернюю особь new. Дочерняя особь занимает место родительской в популяции при
выполнении следующего условия:

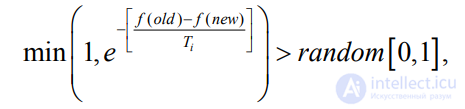
где f(old), f(new) – ФФ родительской и дочерней особей соответственно; random[0, 1] – случайная величина в диапазоне [0, 1]; Ti – температура на i-й итерации алгоритма. Данная модификация позволила несколько улучшить эффективность ПЭГ. Операторы рекомбинации Эти операторы перемещают последовательные участки генома в пределах хромосомы. Три типа таких участков накладывают различные ограничения на операторы. Оператор копирования со сдвигом копирует последовательность символов генома в любую позицию головы гена, кроме первой. Ограничение на первую позицию обусловлено тем, что перемещаемая последовательность может начинаться с терминального символа, помещение которого в корень приведет к вырожденному дереву из одного элемента. Ген–источник копируемой последовательности остается неизменным.

Элементы головы гена–приемника, начиная с позиции, в которую будет скопирована целевая последовательность, сдвигаются для освобождения места, а вышедшие за пределы головы элементы отбрасываются. Оператор копирования со сдвигом в корень отличается от предыдущего тем, что целевая последовательность начинается с элемента– функционала и копируется в корень гена– приемника. Оба оператора копирования вносят значительные изменения и поэтому наравне с мутацией отлично подходят для внесения генетического разнообразия, предотвращая застревание в локальном оптимуме и ускоряя поиск хороших решений. Оператор перестановки генов вносит изменения в результат вычисления декодированного дерева только при условии использования некоммутативной связующей функции в мультигенной хромосоме, такой как «ЕСЛИ, ТО».

Однако преобразующая сила (способность вносить генетическое разнообразие) данного оператора наиболее проявляется в связке с операторами кроссовера. Например, возможно появление дублируемых генов – явление, выполняющее ощутимую роль в биологии и эволюции. Все три вида рекомбинации осуществляют обмен генетическим материалом между двумя родительскими хромосомами, порождая две новые особи. Вероятность того, что будет применен один из трех описанных далее операторов, обычно задают величиной 0,7.

В операторе одноточечной рекомбинации две особи скрещиваются вокруг линии, проходящей через случайным образом выбранную позицию хромосомы. В большинстве случаев полученное потомство проявляет характеристики своих родителей, что делает одноточечную рекомбинацию наиболее часто используемым в ПЭГ оператором, наравне с мутацией. Отличие двухточечной рекомбинации состоит в том, что обмен участками генома происходит между двумя точками. Поскольку преобразующая сила двухточечной рекомбинации выше, чем у одноточечной, она применяется чаще для решения сложных задач с использованием мультигенных хромосом. В генной рекомбинации проводится замена генов, занимающих в обеих хромосомах позицию, определяемую случайным образом. Следует отметить, что использование рекомбинации и/или операторов перемещения как единственного вида применяемых операторов сводится к перемешиванию существующих участков генома и не обеспечивает создание нового генетического материала. Поэтому для решения сложных задач в таком случае может понадобиться популяция большого размера.

Числовые константы в ПЭГ

Создание числовых констант с плавающей запятой необходимо для выполнения символьной регрессии. В стандартном алгоритме ПЭГ для обозначения константы в геноме используется терминальный символ «?», а начальный набор констант представлен доменом DC [10]. Каждый ген располагает собственным массивом, содержащим используемые им константы и заполняемым на основе домена DC при генерации начальной популяции. Численное значение константным символам назначается только при экспрессии генов. Для внесения генетического разнообразия был добавлен специальный оператор мутации констант. Начальный набор возможных числовых констант может быть задан вручную: как перечислением, так и заданием диапазона (успешное решение задач таким методом прямого управления константами возможно только при наличии априорных знаний о решении, позволяющих задать корректный диапазон). Обычно используется метод инициализации значений констант случайными числами.

Динамические константы

В работе [11] предлагается при старте алгоритма ПЭГ на этапе создания новой популяции начальные значения констант в хромосомах отбирать из множества А ={0,1316, 0,2128, 0,3441, 0,5571, 0,9015, 1,4588, 2,3605, 3,8195, 6,1804, 10,0007}, полученного таким образом, чтобы соотношение соседних элементов было золотым сечением. В данной модификации используется следующий оператор мутации каждой константы Cj в геноме выбранной особи:

 Из фиксированного глобального массива первичных констант А случайным образом выбирается константа V.

 Случайным образом выбирается оператор Op из множества {+, —, /, *}.



Плавная и случайная мутация констант

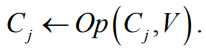
Исследования операторов мутации, основанных на техниках плавной и случайной мутации, описаны в работе [12]. Был задан оператор одноточечной мутации константы: при начальной конфигурации ПЭГ задается отсортированный список возможных констант. Этот оператор изменяет одну символ–константу в гене: при случайной мутации на замену выбирается любой другой элемент списка, при плавной – какой-либо из соседних текущему. Данная операция применяется к каждому гену хромосомы. Локальный поиск должен проводиться в сторону оптимального решения, что означает применение результата мутации только тогда, когда он повышает значение ФФ особи.

Всего было исследовано пять подходов к мутации:

 Плавная мутация лучшей особи в конце расчета поколения.

 Случайная мутация лучшей особи в конце расчета поколения.

 Плавная мутация каждой особи в первые α процента поколений в конце расчета поколения.

 Случайная мутация каждой особи в первые α процента поколений в конце расчета поколения.

 Интервальная случайная мутация: первые g поколений случайной мутации подвергаются все особи популяции в конце расчета поколения.

Применение подхода, при котором мутации подвергается только лучшая особь поколения, никак не повлияло на эффективность алгоритма. Из этого можно сделать вывод, что лучшая особь, полученная стандартным алгоритмом ПЭГ, по определению достаточно хороша и не требует модификаций. Это подтверждает также решающую роль эволюционного процесса ПЭГ (выполнение генетических модификаций и отбор) в поиске оптимальных решений. Применение мутации к каждой особи популяции значительно повышает значение ФФ популяции, особенно в первых поколениях. Однако с течением времени процентное соотношение особей, улучшенных после мутации, уменьшается. Это происходит вследствие того, что спустя определенное количество поколений формируются группы субоптимальных решений, константы которых уже должным образом настроены, поэтому на данном этапе более значимы операторы, приводящие к большим изменениям. Применение методов, использующих мутации констант к каждой особи, приводит к росту времени выполнения алгоритма, однако получение более качественных решений не позволяет напрямую сравнить эффективность таких модифицированных алгоритмов со стандартным ПЭГ. Кроме того, применение упомянутых трех техник к различным задачам не позволило выявить лучшую из них.

Плавно-динамические константы

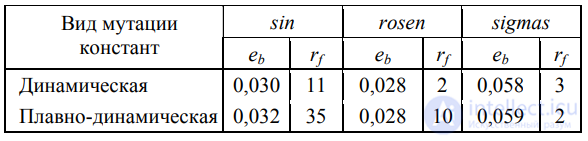
Недостаток описанных операторов мутации численных констант это отсутствие тонкой подстройки коэффициентов особей: степень изменения ничем не ограничена и отсутствуют гарантии поступательного движения в сторону оптимума. Для устранения этого недостатка [13] была построена процедура осуществления направленного процесса эволюции, основанная на комбинации динамического подхода работы с константами ПЭГ и метода иммунных сетей. Создание нового терминала–константы выполняется согласно динамическому подходу: новому узлу (при создании начальной популяции либо после изменения типа узла на терминал– константу оператором мутации) задается значение одно из элементов массива «золотых сечений» А. Оператор плавно-динамической мутации констант изменяет значение в пределах ±10 процентов от текущего:

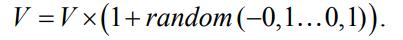
Результаты эксперимента, подтверждающие преимущество такого подхода в сравнении с неограниченной мутацией, приведены в табл. 4.

Таблица 4. Эффективность алгоритма при плавной и динамической мутации констант

Фитнес-функция

Для повышения эффективности отбора в [7, 14] предложено введение порогового значения ФФ. Особи, ФФ которых не достигает этого порогового значения, не допускаются к репродукции. Установка порогового значения требует соблюдения баланса между ускорением сходимости и уменьшением разнообразия, что приводит к преждевременной сходимости. Поэтому целесообразно применять динамический порог, обновляющийся на каждой итерации и представляющий собой среднее значение ФФ популяции, умноженное на коэффициент масштабирования. В большинстве случаев в зависимости от задачи используется значение коэффициента в диапазоне [0,15; 1,5], с оптимальным значением 1,25. Давление на процесс эволюции, оказываемое порогом отбора, положительно влияет на поиск оптимального решения, существенно сокращая время поиска. В схему расчета ФФ в работе [15] добавлен коэффициент давления отбора, отражающий количественную степень влияния возрастания среднеквадратичной ошибки решения на падение его приспособленности

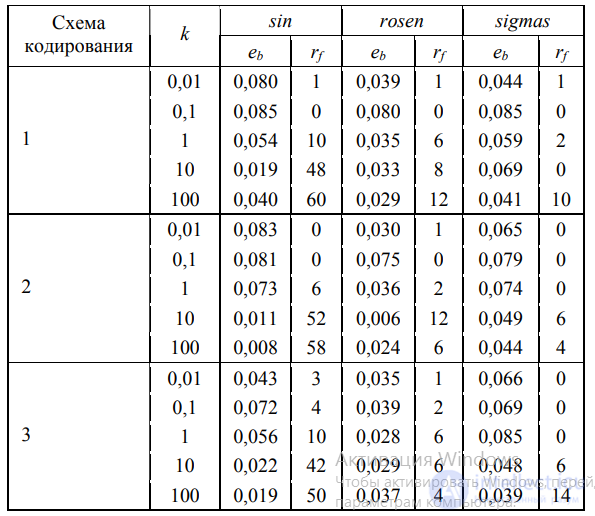
где i – индекс особи в популяции; g – поколение; err i g (, ) – среднеквадратичная ошибка i-го решения; k – коэффициент давления отбора; 1000 – максимальное значение ФФ. На рис. 2 приведен график зависимости ФФ от погрешности (MSE) для различных значений k, а в табл. 5 – влияние значения этого коэффициента на эффективность модификаций алгоритмов.

Анализ результатов экспериментов по сим-вольной регрессии на различных наборах данных позволил определить оптимальное значение коэффициента давления отбора k = 10,0. Данная величина отличается от значения, принятого в исходном алгоритме ПЭГ (k = 100).

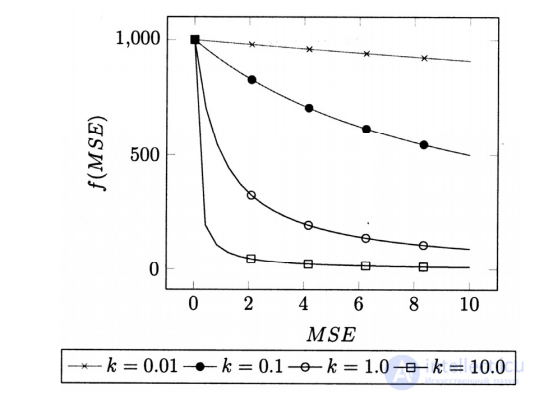
Рис. 2. Графики ФФ для различных значений k

Частичный подсчет фитнес-функции

Главным недостатком как эволюционных алгоритмов в целом, так и ПЭГ в частности есть низкая скорость их работы (в сравнении со скоростью построения искусственных нейронных сетей, регрессионных моделей). Любое ускорение алгоритма ПЭГ позволяет улучшить качество получаемых моделей, так как дает возможность проведения расчета большего количества поколений и выполнения большего числа независимых запусков за эквивалентное время.

Таблица 5. Эффективность алгоритма при различных коэффициентах давления k

Следует отметить, что наиболее ресурсоемкой частью алгоритма есть вычисление ФФ, так как на вход модели подаются все имеющиеся данные, которые затем обрабатываются в соответствии с программой (формулой, правилом), закодированной моделью. В работе [16] удалось получить универсальный метод ускорения процедуры расчета фитнеса, позволивший значительно улучшить оба показателя эффективности (еb и rf) и основанный на следующих соображениях. В формулу расчета ФФ, как правило, входит СКО модели, а само значение ФФ служит для сравнения эффективности моделей между собой. Как оказалось, для такой оценки не требуется вычисление СКО по полному набору подаваемых на вход данных. Если на определенном этапе текущее значение СКО (либо соответствующая ФФ) превысит некоторый порог threshold, дальнейшие расчеты могут быть прерваны. Такой подход позволяет избежать лишних затрат на точное вычисление ФФ плохо приспособленных особей, заменяя его приближенным оценочным значением.

В этом случае весь набор входных данных DataIп во избежание последовательностей соседних точек перемешивается и разбивается на G пакетов :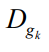

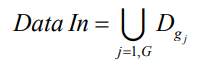
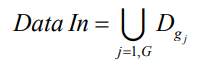
После обработки каждого пакета проводится оценка ФФ, и на ее основании выносится решение о прекращении вычислений особи. Условием прекращения служит сравнение значения ФФ по вычисленным первым К группам с пороговым значением threshold, которое динамически изменяется в процессе эволюции и поэтому задается некоторой долей (например, 0,7) от среднего значения ФФ популяции предыдущего поколения:

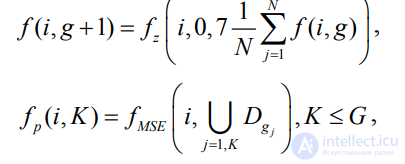
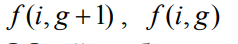– возвращаемое значение ФФ i-й особи рассчитываемого и предыдущего поколений;

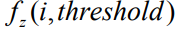
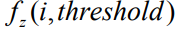– функция взвешенного значения ФФ;

N – размер популяции; К – количество обработанных групп входных данных.

Для внесения различия между особями, расчет которых был прерван в различные моменты времени (пороговое значение ошибки было превышено при разном количестве обработанных групп входных данных), в формулу вводится коэффициент штрафа K/G:

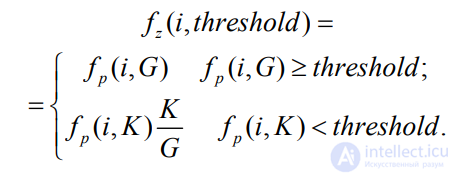
Таким образом, плохие решения будут использовать меньше ресурсов, в то время как лучшие особи будут вычислены наиболее точно. В табл. 6 приведены результаты сравнительного анализа производительности исходных алгоритмов с модифицированными частичным подсчетом СКО.

Таблица 6. Эффективность алгоритма с различными фитнес-функциями

Заключение.

В ходе анализа существующих методов и средств, направленных на ускорение получения модели алгоритмом ПЭГ и повышение ее качества, а также проведенных экспериментов выявлен ряд ограничений производительности традиционного алгоритма, таких как длительность вычисления ФФ, отсутствие тонкой подстройки числовых констант, влияние размера хромосомы на скорость сходимости, проблемы с поиском сложных моделей. Поэтому дальнейшие исследования должны быть направлены на создание методов и подходов, способствующих преодолению данных ограничений.

Вау!! 😲 Ты еще не читал? Это зря!

генетические алгоритмы

А как ты думаешь, при улучшении экспрессия генов, будет лучше нам? Надеюсь, что теперь ты понял что такое экспрессия генов, генетические операторы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Эволюционные алгоритмы