Дифференциальная эволюция кратко

Сразу хочу сказать, что здесь никакой воды про дифференциальная эволюция, и только нужная информация. Для того чтобы лучше понимать что такое дифференциальная эволюция , настоятельно рекомендую прочитать все из категории Эволюционные алгоритмы.

• Дифференциа́льная эволю́ция (англ. differential evolution) — метод многомерной математической оптимизации, относящийся к классу стохастических алгоритмов оптимизации (то есть работает с использованием случайных чисел) и использующий некоторые идеи генетических алгоритмов.

  Это прямой метод оптимизации, то есть он требует только возможности вычислять значения целевой функций, но не ее производных. Метод дифференциальной эволюции предназначен для нахождения глобального минимума (или максимума) недифференцируемых, нелинейных, мультимодальных (имеющих, возможно, большое число локальных экстремумов) функций от многих переменных. Метод прост в реализации и использовании (содержит мало управляющих параметров, требующих подбора), легко распараллеливается.

  Метод дифференциальной эволюции был разработан Рэйнером Сторном и Кеннетом Прайсом, впервые опубликован ими в 1995 году и развит в дальнейшем в их более поздних работах.

  Алгоритм
  В его базовом виде алгоритм можно описать следующим образом. Изначально генерируется некоторое множество векторов, называемых поколением. Под векторами понимаются точки n-мерного пространства, в котором определена целевая функция f(x), которую требуется минимизировать. На каждой итерации алгоритм генерирует новое поколение векторов, случайным образом комбинируя векторы из предыдущего поколения. Число векторов в каждом поколении одно и то же и является одним из параметров метода.

  Новое поколение векторов генерируется следующим образом. Для каждого вектора x_i из старого поколения выбираются три различных случайных вектора v_1, v_2, v_3 среди векторов старого поколения, за исключением самого вектора x_i, и генерируется так называемый мутантный вектор (mutant vector) по формуле:

  v = v_1 + F \cdot (v_2 - v_3),
  где F — один из параметров метода, некоторая положительная действительная константа в интервале [0, 2].

  Над мутантным вектором v выполняется операция «скрещивания» (crossover), состоящая в том, что некоторые его координаты замещаются соответствующими координатами из исходного вектора x_i (каждая координата замещается с некоторой вероятностью, которая также является еще одним из параметров этого метода). Полученный после скрещивания вектор называется пробным вектором (trial vector). Если он оказывается лучше вектора x_i (то есть значение целевой функции стало меньше), то в новом поколении вектор x_i заменяется на пробный вектор, а в противном случае — остается x_i.

  Примеры практических приложений
  Поисковая система Яндекс использует метод дифференциальной эволюции для улучшения своих алгоритмов ранжирования.

Differential Evolution: генетический алгоритм оптимизации функции

Алгоритмы*

Вы уже читали вероятно множество статей, посвященных эволюционным алгоритмам вообще и генетическим алгоритмам в частности. В таких статьях обычно более или менее подробно описывается общая структура и идеология генетического алгоритма, а затем приводится пример его использования. Каждый такой пример включает в себя какой-то выбранный автором вариант процедуры скрещивания особей, мутации и отбора, причем в большинстве случаев для каждой новой задачи приходится придумывать свой вариант этих процедур. Кстати, даже выбор представления элемента пространства решений вектором генов очень сильно влияет на качество получаемого алгоритма и по сути является искусством.

В то же время очень многие практические задачи легко сводятся к оптимизационной задаче на поиск минимума функции nвещественных переменных и для такого типового варианта хотелось бы иметь готовый надежный генетический алгоритм. Об этом говорит сайт https://intellect.icu . Поскольку даже определение операторов скрещивания и мутации для векторов, состоящих из вещественных чисел, оказывается не совсем тривиальным, то «изготовление» нового алгоритма для каждой такой задачи оказывается особенно трудоемким.

Под катом приводится краткое описание одного из самых известных генетических алгоритмов вещественной оптимизации — алгоритма дифференциальной эволюции (Differential Evolution, DE). Для сложных задач оптимизации функции n переменных этот алгоритм обладает настолько хорошими свойствами, что зачастую может рассматриваться как готовый «строительный блок» при решении многих задач идентификации и распознавания образов.



Я буду считать, что читатель знаком с базовыми понятиями, используемыми при описании генетических алгоритмов, поэтому сразу перейду к сути дела, а в заключении опишу наиболее важные свойства алгоритма DE.

Генерация начальной популяции

В качестве начальной популяции выбирается случайный набор из N векторов из пространства Rn. Распределение исходной популяции должно выбираться, исходя из особенностей решаемой оптимизационной задачи — обычно используется выборка изn-мерного равномерного или нормального распределения с заданными математическим ожиданием и дисперсией.

Воспроизводство потомков

На очередном шаге алгоритма производится скрещивание каждой особи X из исходной популяции со случайно выбранной особьюC, отличной от X. Координаты векторов X и C рассматриваются как генетические признаки. Перед скрещиванием применяется специальный оператор мутации — в скрещивании участвуют не исходные, а искаженные генетические признаки особи C:



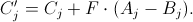
Здесь A и B — случайно выбранные представители популяции, отличные от X и C. Параметр F определяет т.н. силу мутации — амплитуду возмущений, вносимых в вектор внешним шумом. Следует особо отметить, что в качестве шума, искажающего «генофонд» особи C используется не внешний источник энтропии, а внутренний — разность между случайно выбранными представителями популяции. Ниже мы остановимся на этой особенности подробнее.

Скрещивание производится следующим образом. Задается вероятность P, с которой потомок T наследует очередной (искаженный мутацией) генетический признак от родителя C. Соответствующий признак от родителя X наследуется с вероятностью 1 — P. Фактически n раз разыгрывается бинарная случайная величина с математическим ожиданием P, и для единичных ее значений производится наследование (перенос) искаженного генетического признака от родителя C (т.е. соответствующей координаты вектора C'), а для нулевых значений — наследование генетического признака от родителя X. В результате формируется вектор-потомок T.

Отбор

Отбор осуществляется на каждом шаге функционирования алгоритма. После формирования вектора-потомка T производится сравнение целевой функции для него и для его «прямого» родителя X. В новую популяцию переносится тот из векторов X и T, на котором целевая функция достигает меньшего значения (речь идет о задаче минимизации). Здесь необходимо заметить, что описанное правило отбора гарантирует неизменность размера популяции в процессе работы алгоритма.

Обсуждение особенностей алгоритма DE

В целом алгоритм DE представляет собой одну из возможных «непрерывных» модификаций стандартного генетического алгоритма. В то же время этот алгоритм имеет одну существенную особенность, во многом определяющую его свойства. В алгоритме DE в качестве источника шума используется не внешний генератор случайных чисел, а «внутренний», реализованный как разность между случайно выбранными векторами текущей популяции. Напомним, что в качестве исходной популяции используется совокупность случайных точек, выбранных из некоторого генерального распределения. На каждом шаге популяция преобразуется по некоторым правилам и в результате на следующем шаге в качестве источника шума снова используется совокупность случайных точек, но этим точкам соответствует уже некий новый закон распределения. Эксперименты показывают, что в целом эволюция популяции соответствует динамике «роя мошек» (т.е. случайного облака точек), движущегося как целое вдоль рельефа оптимизируемой функции, повторяя его характерные особенности. В случае попадания в овраг «облако» принимает форму этого оврага и распределение точек становится таким, что математическое ожидание разности двух случайных векторов оказывается направленным вдоль длинной стороны оврага. Это обеспечивает быстрое движение вдоль узких вытянутых оврагов, тогда как для градиентных методов в аналогичных условиях характерно колебательная динамика «от стенки к стенке». Приведенные эвристические соображения иллюстрируют наиболее важную и привлекательную особенность алгоритма DE — способность динамически моделировать особенности рельефа оптимизируемой функции, подстраивая под них распределение «встроенного» источника шума. Именно этим объясняется замечательная способность алгоритма быстро проходить сложные овраги, обеспечивая эффективность даже в случае сложного рельефа.

Выбор параметров

Для размера популяции N обычно рекомендуется значение Q * n, где 5 <= Q <= 10.

Для силы мутации F разумные значения выбираются из отрезка [0.4, 1.0], причем хорошим начальным значением будет 0.5, но при быстром вырождении популяции вдали от решения следует увеличить параметр F.

Вероятность мутации P изменяется от 0.0 до 1.0, причем начинать следует с относительно больших значений (0.9 или даже 1.0), чтобы проверить возможность быстрого получения решения случайным поиском. Затем следует уменьшать значения параметра вплоть до 0.1 или даже 0.0, когда в популяции практически не вносится изменчивости и поиск оказывается конвергентным.

На сходимость сильнее всего влияют размер популяции и сила мутации, а вероятность мутации служит для более тонкой настройки.

Численный пример

Особенности метода DE хорошо иллюстрируются при его запуске на стандартной тестовой функции Розенброка вида



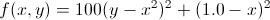
Эта функция имеет очевидный минимум в точке x = y = 1, который лежит на дне длинного извилистого оврага с крутыми стенками и очень пологим дном.

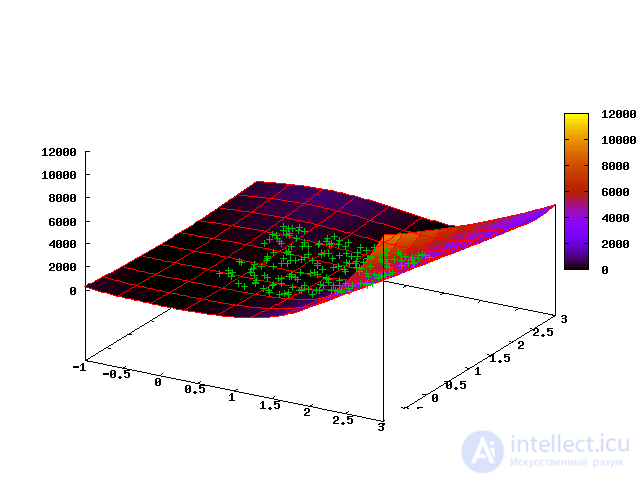
При запуске с равномерным начальным распределением 200 точек в квадрате [0, 2] x [0, 2] после 15 шагов получаем вот такое распределение популяции:



Видно, что «облако» точек расположилось вдоль дна оврага и большинство мутаций будет приводить к сдвигу точек также вдоль дна оврага, т.е. метод хорошо адаптируется к особенностям геометрии пространства решений.

Следующая анимированная картинка показывает эволюцию облака точек на первых 35 шагах алгоритма (первый кадр соответствует начальному равномерному распределению):

Ссылки

• Дамашняя страничка алгоритма содержит много реализаций и примеров использования в разных областях.
• Статья в Dr. Dobb's Journal содержит очень простую и понятную реализацию на языке C, которую можно взять за основу при использовании алгоритма DE в своих проектах.

А как ты думаешь, при улучшении дифференциальная эволюция, будет лучше нам? Надеюсь, что теперь ты понял что такое дифференциальная эволюция и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Эволюционные алгоритмы