n. large fern with an upright trunklike stem.

 ... {. return } visit ( t [ k ]). traverse ( 2 * k + 1 ). traverse ( 2 * k + 2 ). } traverse ( 0 ) } func ( t tree ) iterInorder ( visit func ( int )) {. var traverse func ( int ). traverse = func ... ... {. return } traverse ( 2 * k + 1 ). visit ( t [ k ]). traverse ( 2 * k + 2 ). } traverse ( 0 ) } func ( t tree ) iterPostorder ( visit func ( int )) {. var traverse func ( int ). traverse = func ... (Structures and data processing algorithms.)
... {. return } visit ( t [ k ]). traverse ( 2 * k + 1 ). traverse ( 2 * k + 2 ). } traverse ( 0 ) } func ( t tree ) iterInorder ( visit func ( int )) {. var traverse func ( int ). traverse = func ... ... {. return } traverse ( 2 * k + 1 ). visit ( t [ k ]). traverse ( 2 * k + 2 ). } traverse ( 0 ) } func ( t tree ) iterPostorder ( visit func ( int )) {. var traverse func ( int ). traverse = func ... (Structures and data processing algorithms.)
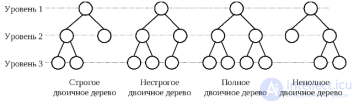
 ... .; copy thedata (except forlinks tochild elements ) from .mton ; recursively remove thenode m.Tree Traversal (TRAVERSE ).There arethree tree traversal operations thatdiffer inthe.traversal order ... ... thisfunction fortheroot , thenitstarts it.fortheright subtree INFIX TRAVERSE (tr ) - bypass theentire tree , following theorder . (left subtree , vertex , right subtree ).Items ascending PREFIX ... (Structures and data processing algorithms.)
... .; copy thedata (except forlinks tochild elements ) from .mton ; recursively remove thenode m.Tree Traversal (TRAVERSE ).There arethree tree traversal operations thatdiffer inthe.traversal order ... ... thisfunction fortheroot , thenitstarts it.fortheright subtree INFIX TRAVERSE (tr ) - bypass theentire tree , following theorder . (left subtree , vertex , right subtree ).Items ascending PREFIX ... (Structures and data processing algorithms.)
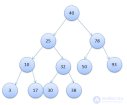
 ... illustrates the sequence of calling the intrave ( tree ) procedure . as you traverse the nodes of the simplest tree shown .in Figure ... ... . q: = p; if key ... (Structures and data processing algorithms.)
... illustrates the sequence of calling the intrave ( tree ) procedure . as you traverse the nodes of the simplest tree shown .in Figure ... ... . q: = p; if key ... (Structures and data processing algorithms.)
... the final node . (null pointer ) The following listing shows functions that traverse the tree in. width and depth void preorder (struct tree * root ). { if ( root ) return ; if (root ... ... , search functions are easily implemented The following function returns a pointer to the top of. the tree , in which the information matches the search key ,.or zero ( NULL ) if there is no such vertex struct tree ... (Structures and data processing algorithms.)
 ... (first incoming parent edge , then first child .edge , etc ), this yields an embedding of the tree in the plane ., unique up to ambient isotopy Conversely , such an embedding determines an ordering of the child ... ... with X',. s' coincides with path popping , and t' is the identity on X'. Like with apgs , unfolding is idempotent and always results in. a tree The underlying apg is obtained as the structure (X, R, t(ar )). where R = {(t(a),s(a)) | a ∈ A \ {ar }}. The diagram ... (Structures and data processing algorithms.)
... (first incoming parent edge , then first child .edge , etc ), this yields an embedding of the tree in the plane ., unique up to ambient isotopy Conversely , such an embedding determines an ordering of the child ... ... with X',. s' coincides with path popping , and t' is the identity on X'. Like with apgs , unfolding is idempotent and always results in. a tree The underlying apg is obtained as the structure (X, R, t(ar )). where R = {(t(a),s(a)) | a ∈ A \ {ar }}. The diagram ... (Structures and data processing algorithms.)
 ... .ofPSh Gabdrakhmanova , devoted tothestudy ofthedaily life of.medieval peasants onthematerial offamily trees (Flanders , XII .century ) PSh Gabdrakhmanov notes thatthehistory oftheprivate life of.medieval ... ... andfeatures willbecome , asthey.say , amatter oftechnique Appendix Information about thecharacters ofthegenealogical tree of.MOZheltoukhova (St Petersburg State Attestation Commission , 1992 /93 academic year ... (Sociology)
... .ofPSh Gabdrakhmanova , devoted tothestudy ofthedaily life of.medieval peasants onthematerial offamily trees (Flanders , XII .century ) PSh Gabdrakhmanov notes thatthehistory oftheprivate life of.medieval ... ... andfeatures willbecome , asthey.say , amatter oftechnique Appendix Information about thecharacters ofthegenealogical tree of.MOZheltoukhova (St Petersburg State Attestation Commission , 1992 /93 academic year ... (Sociology)
Комментарии
Оставить комментарий