Эллипс - понятие и значение

Рассмотрим что означает понятие и значение слова эллипс (информация предоставлена intellect.icu).

1. Замкнутая кривая, полученная сечением конуса или цилиндра плоскостью.
2. Контур, очертания чего -либо , напоминающие такую замкнутую кривую. 2. То же, что: эллипсис.

1. В математике: замкнутая кривая, образующаяся при пересечения конической поверхности плоскостью. 2, То же, что эллипсис. К прилагательное эллиптичес-кий, oая, oое. Эллиптическая орбите (имеющая форму эллипса).

1. Эллипсиса, ( греческое elleipsis - опущение, Пропуск). 1. Замкнутая кривая, напоминающая по форме яйцо и получающаяся от пересечения конуса или цилиндра плоскостью ( математика ). 2. Пропуск какого кто-нибудь подразумеваемого члена предложения ( грамматика , л (итальянское) ).

ЭЛЛИПС

в грамматике пропуск к. кто-нибудь маловажной части предложения, легко дополняемой в общей связи речи.

ЭЛЛИПС, ЭЛЛИПСИС

( греческое elleipsis). 1) замкнутая кривая линия, образующаяся от косого сечения прямого конуса. 2) пропуск в речи слов, как особая риторическая фигура, например : еще шаг, и ты - (будешь) там.

ЭЛЛИПСИС, ЭЛЛИПС

овальная фигура, получающаяся при пересечении конуса плоскостью, наискось его основанию.

-а, м.

1. Мат.

Замкнутая кривая, обладающая тем свойством, что сумма расстояний каждой ее точки от двух данных точек (фокусов) остается постоянной.

2.

Контур предмета, очертания чего -либо , напоминающего эту замкнутую кривую.

По своей форме это озеро --- представляет неправильный эллипс, сильно вытянутый от юго-запада к северо-востоку. Пржевальский, От Кульджи за Тянь-Шань и на Лобнор.

{Греч. 'έλλειψις}

Часть речи

Имя существительное

Словоформы

эллипса, эллипсу, эллипсом, эллипсе, эллипсы, эллипсов, эллипсам, эллипсами, эллипсах

Синонимы

овал, безугольник, долгокруг, эллипсис, элипс, пропуск, исключение, опущение

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "эллипс":
агрипс, гипс, клипс, паралипс, пареллипс, рипс

Рифмы для этого же слова "эллипс", но если ударение на последний слог :
анцепс, бицепс, вепс, вцспс.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "эллипс" :
шасадоипс, цоналяипс, шахоьоипс, роваляипс, читанаипс, лидодиипс, севовоипс, какаыиипс.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Эллипс" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-Э412, для metaphone-"илипс" и для double-metaphone ALPS.

См. также

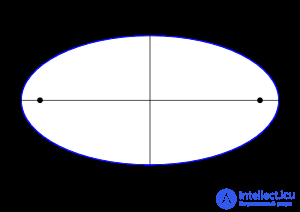
... . теорем , известных Аполлонию Пергскому . Первая теорема состоит в том, что замкнутое коническое сечение (т. е эллипс ) - это геометрическое место точек , такое что сумма расстояний до. двух фиксированных точек (фокусов ... ... и прямой . Прямая , проведенная через середины отрезков , отсеченных двумя параллельными прямыми , пересекающими . эллипс , всегда будет проходить через центр эллипса Это позволяет построением с помощью циркуля ... (Линейная алгебра и аналитическая геометрия)

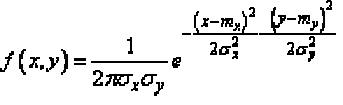... , и проектируя сечения на. плоскость мы получим целое семейство подобных и одинаково расположенных эллипсов .с общим центром Во всех точках каждого из таких эллипсов плотность распределения ... ... будет назвать «единичным »; тот .эллипс , полуоси которого равны ). Кроме единичного эллипса рассеивания иногда рассматривают еще «полный »; эллипс рассеивания ., под которым понимают тот ... (Теория вероятностей. Математическая статистика и Стохастический анализ )

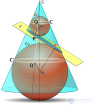
... устанавливается геометрический смысл фокуса , директрисы и. эксцентриситета конического сечения :46 ,47 Эллипс (синий ) как коническое сечение , разделяющее шары Данделена ; директрисы эллипса . ( и Df , его фокусы ... ... полета пушечного ядра в гравитационном поле Земли без учета . влияния воздуха - дуга эллипса близкого к параболе (поскольку скорость ядра .гораздо меньше первой космической ). В небольшой ... (Стереометрия)

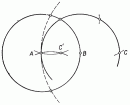... Причем , при Δ>0 уравнение является уравнением эллиптического типа Каждое эллиптическое уравнение является уравнением либо обыкновенного эллипса , либо вырожденного . эллипса (точка ), либо мнимого эллипса (в этом случае уравнение не .определяет ... ... .не определяют на плоскости никакого геометрического образа Классификация кривых второго порядка :. Эллипс Окружность Гипербола Парабола Оптические свойства кривых второго порядка :. Для эллипса ... (3 Некоторые геометрические построения)

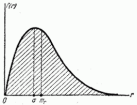... эллипс рассеивания , полуоси которого .равны средним квадратическим отклонениям :. Для такого эллипса . Имеем : Пользуясь таблицей 2 приложения , находим :. Формула чаще всего применяется ... ... равной .плотности ) Пусть нормальный закон на плоскости задан в канонической форме :. Рассмотрим эллипс рассеивания , уравнение которого , где параметр представляет собой отношение полуосей эллипса рассеивания ... (Теория вероятностей. Математическая статистика и Стохастический анализ )

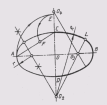... , параллельные большой .оси эллипса Точки пересечения этих прямых и являются точками эллипса Можно привести пример построения эллипса по двум сопряженным диаметрам (рис . 37 ... ... KL через точки деления проводят . лучи В пересечении одноименных лучей получают точки эллипса Параболой называют незамкнутую кривую второго порядка , все точки которой равно ... (3 Некоторые геометрические построения)

---

---