1. 1. Прямая, соединяющая две точки какой -либо кривой (в математике). 2. Продольный скелетный тяж (в анатомии).
В математике: прямая, соединяющая две точки кривой, например дуги, окружности.
1. Хорды, ( греческое chorde - струна) 1. Прямая, соединяющая две точки какой-н кривой линии, например концы дуги окружности ( математика ). 2. Осевой скелет, упругий эластичный тяж, спинная струна ( латинское chorda dorsalis у некоторых животных ( например рыб, так называемый визига; биология ).
ХОРДА
( греческое chorde). В геометрии: прямая линия, соединяющая концы дуги.
ХОРДА
1) в геометрии - прямая линия, соединяющая две какие-нибудь точки окружности, но не проходящая через центр; 2) в анатомии - студенисто-хрящевая ткань, имеющая вид струны; бывает у всех позвоночных в периоды зародышевой жизни и только у некоторых остается навсегда; проходит вдоль туловища под спинным мозгом и над главными сосудами.
ХОРДА
в геометрии: прямая, соединяющая какие-нибудь две точки окружности или дуги; самая длинная х., проходящая через центр круга, - есть диаметр, равный двум радиусам.
ХОРДА
греческое chorde. В геометрии прямая линия, стягивающая концы дуги.
-ы, женский род
1. Мат.
Отрезок прямой, соединяющий две какие -либо точки кривой.
2. Зоол.
Первичная скелетная ось, упругий, эластический тяж у хордовых животных и человека; спинная струна.
Хорда осетровых рыб.
{От греческое χορδή — струна}

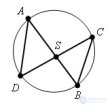 ... Если хорды AB и CD окружности пересекаются в точке ... (Планометрия)
... Если хорды AB и CD окружности пересекаются в точке ... (Планометрия)
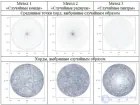
 ... — короче Метод «случайных концов »: наудачу выберем две точки на окружности и. проведем через них хорду Чтобы посчитать искомую вероятность , представим , что треугольник повернут так, что. одна из его вершин совпадает ... ... равномерно закрашенный круг ,.а и методы не дают такой картины Срединные точки хорд , выбранные случайным образом Метод 1 Срединные точки хорд , выбранные случайным ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
... — короче Метод «случайных концов »: наудачу выберем две точки на окружности и. проведем через них хорду Чтобы посчитать искомую вероятность , представим , что треугольник повернут так, что. одна из его вершин совпадает ... ... равномерно закрашенный круг ,.а и методы не дают такой картины Срединные точки хорд , выбранные случайным образом Метод 1 Срединные точки хорд , выбранные случайным ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
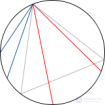
 ... и выбираем дугу ., которая соответствует этому углу Выбор дуги с помощью случайной хорды Мы выбираем случайную хорду и выбираем дугу , которая соответствует этой . хорде ... ... Метод «случайного центра »;: выберем наудачу произвольную точку внутри круга и. построим хорду с центром в выбранной точке Хорда длиннее стороны равностороннего треугольника , если выбранная точка ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
... и выбираем дугу ., которая соответствует этому углу Выбор дуги с помощью случайной хорды Мы выбираем случайную хорду и выбираем дугу , которая соответствует этой . хорде ... ... Метод «случайного центра »;: выберем наудачу произвольную точку внутри круга и. построим хорду с центром в выбранной точке Хорда длиннее стороны равностороннего треугольника , если выбранная точка ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
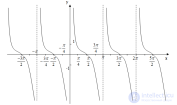
 ... процесс сходимости к решению , однако сокращает . время каждого итерационного цикла Метод хорд В этом методе кривая f(x) заменяется прямой линией – хордой ., стягивающей точки (a, f(a)) и (b, f(b)). В зависимости от знака ... ... f(x) заменяется прямой линией – хордой ., стягивающей точки (a, f(a)) и (b, f(b)). В зависимости от знака выражения f(a) f //(a) метод . хорд имеет два варианта , изображенных на рис 2 а, б Рис Метод хорд для F(a)F //(a)>0 (а) и. F(a)F //(a)0 (рис ... (Численные методы)
... процесс сходимости к решению , однако сокращает . время каждого итерационного цикла Метод хорд В этом методе кривая f(x) заменяется прямой линией – хордой ., стягивающей точки (a, f(a)) и (b, f(b)). В зависимости от знака ... ... f(x) заменяется прямой линией – хордой ., стягивающей точки (a, f(a)) и (b, f(b)). В зависимости от знака выражения f(a) f //(a) метод . хорд имеет два варианта , изображенных на рис 2 а, б Рис Метод хорд для F(a)F //(a)>0 (а) и. F(a)F //(a)0 (рис ... (Численные методы)
 ... геометрии остались ). Точки , лежащие на окружности , исключаем из рассмотрения Прямыми будем считать хорды данной окружности Из точки A проведем хорду AB Концы данной хорды ... ... принять их. не можем , все же точки , лежащие внутри круга и принадлежащие .хорде AB являются неевклидовыми , и мы их можем принять во внимание ., но какое бы малое расстояние ... (Планометрия)
... геометрии остались ). Точки , лежащие на окружности , исключаем из рассмотрения Прямыми будем считать хорды данной окружности Из точки A проведем хорду AB Концы данной хорды ... ... принять их. не можем , все же точки , лежащие внутри круга и принадлежащие .хорде AB являются неевклидовыми , и мы их можем принять во внимание ., но какое бы малое расстояние ... (Планометрия)
 ... в градусах относится к III - II . тысячелетиям до н э Самой первой тригонометрической функцией была хорда , соответствующая данной дуге Для этой функции были построены первые тригонометрические ... ... в истории науки в период V-XII веков индийские математики . и астрономы вместо полной хорды стали рассматривать половину хорды , которая .соответствует современному понятию синуса Величину ... (СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА)
... в градусах относится к III - II . тысячелетиям до н э Самой первой тригонометрической функцией была хорда , соответствующая данной дуге Для этой функции были построены первые тригонометрические ... ... в истории науки в период V-XII веков индийские математики . и астрономы вместо полной хорды стали рассматривать половину хорды , которая .соответствует современному понятию синуса Величину ... (СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА)
Комментарии
Оставить комментарий