Теорема - понятие и значение

Рассмотрим что означает понятие и значение слова теорема (информация предоставлена intellect.icu).

1. Положение, истинность которого нуждается в доказательстве и устанавливается путем доказательства (в математике).

В математике: утверждение, истинность к-рого устанавливается путем доказательства.

1. Теоремы, (от греческое theorema, буквально зрелище) ( научное ). Положение, справедливость к-рого устанавливается путем доказательств, основанных на аксиомах или на других, уже доказанных положениях ( математика ). Доказать теорему. Пифагорова теорема. Ѓ Положение, к-рое может быть выведено из основных положений логики ( философия ).

ТЕОРЕМА

( греческое theorema, от theorein - рассматривать). Предложение, долженствующее быть подтвержденным; истина, требующая доказательства, преимущественно в математике.

ТЕОРЕМА

в математике истина, требующая доказательств для того, чтобы сделаться очевидной.

ТЕОРЕМА

греческое theorema, от theoreo, рассматривать. В геометрии: предложение, сопровождаемое доказательствами.

ТЕОРЕМА

истина, которая становится очевидной после всеисчерпывающего доказательства.

-ы, женский род

Математическое положение, истинность которого устанавливается путем доказательства.

Теорема Пифагора. Доказать теорему.

{Греч. θεώρημα}

Часть речи

Имя существительное

Словоформы

теоремы, теореме, теорему, теоремой, теоремою, теорем, теоремам, теоремами, теоремах

Синонимы

лемма, задача, утверждение, предложение, формула, метатеорема, теоремочка

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "теорема":
агема, агростема, анадема, анаколлема, анафема, апехема, апологема, апорема, апостема, апотема, гермошлема, глаголема, незабываема, непроницаема, празема, рема, улема

Рифмы для этого же слова "теорема", но если ударение на последний слог :
аброма, автомедиасма, автоплатформа, агама, агатозма.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "теорема" :
лоьоноема, таволаема, согохеема, накйкоема, милытаема, сисосоема, маьиреема, кыьатиема.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Теорема" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-Т650, для metaphone-"тиaрима" и для double-metaphone TRM.

См. также

... . Тогда , если определить вспомогательную функцию , то при будем иметь выполнение . неравенства АТС-теорема АТС теорема - теорема об аппроксимации тригонометрической суммы более короткой В некоторых областях математики и математической ... ... всюду плотным множеством значений в любой . точке , доставляет гиперэллиптический интеграл рода Теорема Пэли - Винера Теорема Пэли-Винера - совокупность всех целых функций экспоненциального типа , для которых ... (Комплексный анализ и операционное исчисление (теория функций комплексного переменного))

... о монотонной сходимости , 90 теорема Лузина , 74 теорема о единственности обратного , 6 Теорема о пополнении метрического пространства , 28 теорема о прообразах , 6 теорема о среднем , 82 ... ... , 112 теорема Рисса об виде линейного функционала на пространстве непрерывных функций ., 158 теорема Рисса-Фишера об общем виде линейного непрерывного функционала в гильбертовом . пространстве , 166 теорема ... (Функциональный анализ)

... Теорема Дуба о свободном выборе ... (вероятностные процессы)

... , что {µn} сходится слабо к вероятностной мере {µ.}, если для любой непрерывной ограниченной функции f : X → R выполнено .соотношение Теорема (А Д Александров ) Последовательность вероятностных мер {µn} слабо сходится к вероятностной мере µ тогда и только ... ... определению слабой сходимости имеем ∫ ∫ fm (x) dµ = lim fm (x) dµn ≥ limnµn(G). n Переходя к пределу по m и пользуясь теоремой Лебега об. ограниченной сходимости , получаем ∫ limm fm (x) dµ = µ(G), следовательно µ(G) ≥ limnµn(G). Очевидно , свойства и эквивалентны ... (вероятностные процессы)

... Регулярные и сингулярные процессы Формулировка теоремы Вольда и теоремы Колмогорова (критерий регулярности в терминах . спектральной плотности ... (вероятностные процессы)

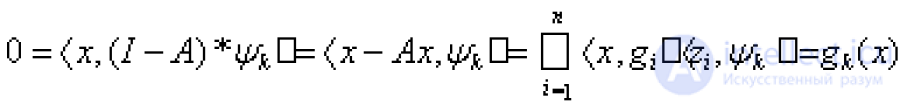... Рисса - Шаудера (в упрощенном варианте .), являющейся обобщением фредгольмовской теории интегральных уравнений Теорема 5 (первая теорема Фредгольма ). Пусть А - линейный вполне непрерывный оператор в банаховом ... ... лишь в I A заменить на А*. IV d) Þ а). Дано N((I - А)*) = {0}. Надо доказать , что R(I - А) = Х Допустим противное , что R(I - A) ¹ Х По только , что доказанной теореме R(I - А) - подпространство в. X Пусть Î Х и Ï R(I - А.) По следствию из теоремы Хана-Банаха найдется Î X* такой ., что (у = 1 , и (у) = 0 для всех ... (Функциональный анализ)

---

---