Сходящийся - понятие и значение

Рассмотрим что означает понятие и значение слова сходящийся (информация предоставлена intellect.icu).

Тоже самое что слово - сближаться,

1. Не совершенный вид
2. Перемещаться на более близкое расстояние, приближаться друг к другу.
3. Вступать в близкие отношения, становиться близкими друг другу.
4. Становиться похожими.
5. Страд. к глагол : сближать.

1. Сближаюсь, сближаешься, несовершенный вид 1. Не совершенный вид к сблизиться. 2. Страд. к сближать.

-аюсь, -аешься; несовершенный вид

1.

Не совершенный вид к сблизиться.

2.

Страд. к сближать.

Синонимы

дружить, сводиться, раздвигаться, сталкивавшийся, сталкивающийся, сходившийся, сводившийся, сводящийся, сдвигавшийся, сдвигающийся, братавшийся, братающийся, роднившийся, роднящийся, сплачивавшийся, сплачивающийся, сживавшийся, сживающийся, породнявшийся, сводивший дружбу, сдружавшийся, сдружающийся, спихивавшийся, спихивающийся, сближаться

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "сходящийся":
беснующейся, беснующийся, бракосочетавшийся, брачующийся, быстропортящийся, вайся, ввалившийся, вертящийся, взбунтовавшийся, взметавшийся, вкоренившийся, захлёбывавшейся, мятущейся, незадавшейся, организуйся, покосившейся, растерявшейся, свихнувшейся, шатающейся, экзаменующейся, экзаменующийся

Рифмы для этого же слова "сходящийся", но если ударение на последний слог :
абонироваться, абсолютизироваться, абсорбироваться, абстрагироваться, авансироваться.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "сходящийся" :
наниняйся, мосыройся, хулувойся, вамятайся, вухорийся, ьаващуйся, сиросойся, вахепайся.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Сходящийся" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-С322, для metaphone-"схaдaщийсa" и для double-metaphone SKTX.

См. также

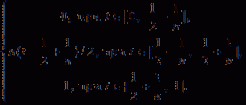... пространстве предельными для множества являются такие точки ., для которых существует последовательность точек множества сходящаяся к х.Замкнутый шар S[a, r] есть замкнутое множество В самом деле , пусть xn S[a, r] и xn . → x Тогда ... ... } - сходится к х;. Любая подпоследовательность {xn } сходится х;. Для любой подпоследовательности { } существует подпоследовательность { } сходящаяся к х;. 4 {xn } - фундаментальная и любая подпоследовательность { } сходится к х;. {xn } - фундаментальная и существует подпоследовательность ... (Функциональный анализ)

... ряд сходится абсолютно , если сходится . ряд из модулей (абсолютных величин ) его членов :. Абсолютно сходящийся ряд сходится и в обычном смысле этого понятия . При этом всякий такой ряд ... ... .случае - расходящимся ) Ряды всегда можно почленно складывать или вычитать , причем сумма и. разность сходящихся рядов также сходятся Если члены рядов берутся из кольца или поля , то ряды ... (Ряды)

... M вероятностных мер слабо компактно , если. из любой последо - вательности {µn} ⊂ M можно выделить слабо сходящуюся подпоследовательности Строго говоря , это свойство следует называть слабой секвенциальной компактностью Впрочем ... ... , что X ⊂ Y и любая мера . µ продолжается на все Y по формуле µ(A) = µ.(A∩X), A ⊂ Y. Можно выделить последовательность мер {µn}, слабо сходящуюся на Y к мере ν Возьмем последовательность компактов Km ⊂ X, т ч 1 sup µ(X \ Km ) ≤. µ∈M m Тогда по свойству ... (вероятностные процессы)

... линейных непрерывных функционалов , 129 пространство ограниченных числовых последовательностей , 12 пространство сходящихся к нулю последовательностей , 13 процесс ортогонализации Шмидта , 116 прямая сумма пространств ... (Функциональный анализ)

... . и непрерывна при a ≤ x < c и c < x ≤ b ,.то Несобственный интеграл от функции , имеющей бесконечный разрыв на интервале интегрирования ., называется сходящимся , если существуют оба предела : и расходящимся , если хотя .бы один из этих пределов не существует ... (Математический анализ. Интегральное исчисление)

... (Вейерштрасса ). Если функция f(x) непрерывна на отрезке [а, b], то. существует последовательность многочленов {(х)}, равномерно на отрезке [а, b].сходящаяся к f(x), т е для любого e > 0 найдется многочлен (х) с номером . n, зависящим от e, такой , что |Pn (x) - f(x)| ... ... , 2 ., функция Рп (х) есть многочлен степени , причем {(х.)} и является искомой последовательностью многочленов , равномерно сходящейся на отрезке [0,.к функции f(x). Так как изучаемая функция f(x) равна нулю за пределами . сегмента [0, , то для любого ... (Функциональный анализ)

---

---