Стереометрия - понятие и значение

Рассмотрим что означает понятие и значение слова стереометрия (информация предоставлена intellect.icu).

1. Раздел элементарной геометрии, изучающий фигуры, лежащие в пространстве.

Раздел геометрии, изучающий фигуры, лежащие в пространстве.

1. Стереометрии, (от греческое stereos-плотный и metreo-мерю) ( математика ). Геометрия в пространстве, отдел геометрии, в к-ром изучаются фигуры, не лежащие в одной плоскости, в отличие от планиметрии.

СТЕРЕОМЕТРИЯ

( греческое , от stereos - плотный, и metreo - меряю). Часть геометрии, трактующая о свойстве твердых тел, находящихся не на плоскостях, противоположная планиметрии.

СТЕРЕОМЕТРИЯ

греческое , от stereos, плотный, и metreo, меряю. Часть геометрии, занимающаяся телами.

СТЕРЕОМЕТРИЯ

смотри геометрия.

СТЕРЕОМЕТРИЯ

часть геометрии, рассматривающая отношение линий и плоскостей в пространстве, определение объемов геометрических тел и проч.

-и, женский род

Раздел элементарной геометрии, в котором изучаются фигуры в пространстве.

{От греческое στερεός — пространственный и σκοπέω — мерю}

Часть речи

Имя существительное

Словоформы

стереометрии, стереометрию, стереометрией, стереометриею, стереометрий, стереометриям, стереометриями, стереометриях

Синонимы

геометрия, математика

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "стереометрия":
абецедария, аблефария, авария, австерия, автометрия, агенория, агеометрия, агиолатрия, агронометрия, агрохимлаборатория, ария, безветрия, гонорария, кюрия, люпозория, маловерия, поветрия, полушария, прелиминария, профилактория

Рифмы для этого же слова "стереометрия", но если ударение на последний слог :
абазия, абакция, абалиенация, абаннация, абартикуляция.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "стереометрия" :
налирерия, ыавасория, ришянирия, ликасирия, резывория, ыамежурия, суларирия, неьезирия.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Стереометрия" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-С365, для metaphone-"стириaмитриa" и для double-metaphone STRM.

См. также

... Основы стереометрии Стереометрия Аксиомы стереометрии Плоскость и точка Плоскость и прямая Параллельность прямых и плоскостей ... (Стереометрия)

... Стереометрия – раздел геометрии , в котором изучаются фигуры в пространстве Основными фигурами в пространстве являются ... (Стереометрия)

... Система аксиом стереометрии состоит из аксиом планиметрии и 3 следующих .: Какова бы ни была плоскость , существуют ... (Стереометрия)

... »;) - в планиметрии прямые ., которые не пересекаются , сколько бы их ни продолжали в обе .стороны В стереометрии две прямые называются параллельными , если лежат в одной . плоскости и не пересекаются Две ... ... . прямой , по одну сторону от нее , есть прямая , параллельная данной Построение параллельных прямых В стереометрии В планиметрии две различные прямые либо пересекаются , либо параллельны В стереометрии возможен ... (Планометрия)

... Пирамидой называется многогранник , который состоит из плоского многоугольника - основания пирамиды ., точки , не лежащей в плоскости основания , - вершины пирамиды и всех .отрезков , соединяющих вершину пирамиды с точками основания Отрезки , соединяющие вершину пирамиды с вершинами основания , называются боковыми ребрами . - основание пирамиды , S - вершина пирамиды , , , ,. - ребра пирамиды Высотой пирамиды называется перпендикуляр , опущенный из вершины пирамиды на плоскость . основания См ... (Стереометрия)

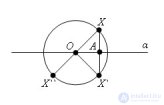... в планиметрии Рис 25 Рис 26 Все сказанное там дословно повторяется в стереометрии Напомним определения Точки А и А называются симметричными относительно точки О, если. точка О делит отрезок ... (Стереометрия)

---

---