Раскрошить - понятие и значение

Рассмотрим что означает понятие и значение слова раскрошить (информация предоставлена intellect.icu).

1. Сов. переходный
2. Превратить в крошки, разделить на мелкие части; размельчить.
3. Размельчив, рассыпать.

СЯ смотри крошить, -ся.

1. Раскрошу, раскрошишь, совершенный вид (к раскрашивать 2), что. Разделить, раздробить на мелкие части, крошки, кусочки, размельчить. Раскрошить хлеб. Раскрошить табак.

-крошу, -крошишь; причастие страдательное (причастие) прошедшее время раскрошенный, -шен, -а, -о; совершенный вид , переходный Раздробить на мелкие части, превратить в крошки.

Раскрошить хлеб.

Осыпанная пылью раскрошенного пулей бетона, тень метнулась в сторону и нырнула в темноту. Н. Островский, Как закалялась сталь.

{Тоня} раскрошила голубям захваченную из дому булочку. Кочетов, Журбины.

Часть речи

Глагол (инфинитив)

Синонимы

раздробивший, раздробленный, измельченный, измельчивший, искрошенный, искрошивший, размельченный, размельчивший

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "раскрошить":
авралить, алаборить, алифить, алырить, анатомить, арканить, атаманить, багрить, багрянить, базанить, продубить, свербить, секьюрить

Рифмы для этого же слова "раскрошить", но если ударение на последний слог :
аббатствовать, абдуцировать, абецедировать, аблактировать, абонировать.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "раскрошить" :
литатеить, насекиить, ыюзуваить, ьыкекаить, сйладаить, титоноить, нораыаить, каьагоить.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Раскрошить" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-Р262, для metaphone-"раскрaшит" и для double-metaphone RSKR.

См. также

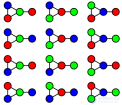... всегда дает правильную раскраску , так. что Единственный вид графов , которые могут быть раскрашены одним цветом - это. нулевые графы Полный граф , состоящий из вершин требует цветов ... ... точно По теореме 4 цветов , любой плоский граф может быть раскрашен . 4 цветами графы - это двудольные графы , в том числе и деревья . Граф является двудольным в том и только ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

... циклов нечетной длины Жадная раскраска показывает , что любой граф может быть раскрашен при. использовании на один цвет больше , чем его максимальная степень вершины ,. Полные графы имеют ... ... может быть сколь угодно плохим .; например , корона с n вершинами может быть раскрашена 2 цветами ,.но существует порядок вершин , который приводит к жадной раскраске из } цветов ... (Алгоритмы и теория алгоритмов)

... красками так, чтобы любые .две области , имеющие общий участок границы , были раскрашены в разные цвета . При этом считается , что каждая область является односвязной , а под. общим участком границы ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

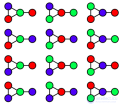... , имели разные цвета . Так как графы , в которых есть петли , не могут быть . раскрашены таким образом , они не являются предметом обсуждения Терминология , в которой метки называются цветами ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

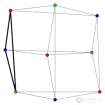... из хорошо известных совершенных графов :. Двудольные графы - граф , который может быть раскрашен в два цвета . Семейство включает леса , графы без циклов Реберные графы двудольных ... ... минимальную границу хроматического числа ., поскольку в клике все вершины должны быть раскрашены в разные .цвета Совершенные графы - это те, у которых нижняя граница точна не . только ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

... показывает , что граф с n вершинами , который можно . раскрасить в два цвета , может быть раскрашен жадным алгоритмом в.цветов Жадные алгоритмы не всегда хороши , например граф ... (Алгоритмы и теория алгоритмов)

---

---