Тоже самое что слово - микрофон,
1. Устройство, преобразующее звуковые колебания в электрические и служащее для передачи звуков на большие расстояния или для их усиления в телефонных аппаратах, системах радиовещания и звукозаписи.
Прибор, преобразующий звуковые колебания в электрические для усиления звучания. Электродинамический м.
1. Микрофона, (от греческое mikros - малый и phone - звук) ( физика ). Прибор для преобразования звуковых колебаний в колебания силы электрического тока. Говорить в микрофон.
МИКРОФОН
( греческое ). Прибор, изобретенный Hughes'ом, в 1878 г., для усиления восприятия бесконечно слабых звуков и шумов; усовершенствован Эдисоном.
МИКРОФОН
прибор для усиления звуков, действует электричеством; изобретет Юзом; употребляется вместе с телефоном и другими приборами.
МИКРОФОН
электрический прибор, служащей для обнаружения и усиления слабых звуков; изобретен Юзом, 1878 г., а усовершенств. Эдисоном.
-а, м.
Прибор, преобразующий звуковые колебания в электрические (применяется при передаче звуков на большие расстояния или для их усиления).
{От греческое μικρός — малый и φωνή — звук}

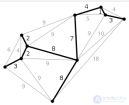 ... задача может быть сформулирована в терминах теории графов как. задача о нахождении минимального остовного дерева в графе , вершины которого .представляют города , ребра - это пары городов , между которыми ... ... конечное число шагов будут обработаны все узлы сети и. построено минимальное остовное дерево Cn =X, =f Пример построения минимального остовного дерева для сети Пример Интернет ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)
... задача может быть сформулирована в терминах теории графов как. задача о нахождении минимального остовного дерева в графе , вершины которого .представляют города , ребра - это пары городов , между которыми ... ... конечное число шагов будут обработаны все узлы сети и. построено минимальное остовное дерево Cn =X, =f Пример построения минимального остовного дерева для сети Пример Интернет ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)
 ... Vol 9 , No 3 , 277-292 ): построить для графа дерево со свойствами минимального остовного . дерева и дерева кратчайших путей Другой важной задачей является быстрое обновление минимального ... ... же .сумму весов ребер , повторяя это, мы получим T таким образом ,. также является максимальным остовным деревом Докажите это утверждение :. предположим , что это не так, в цикле мы должны иметь . только ... (Классические алгоритмы онлайн)
... Vol 9 , No 3 , 277-292 ): построить для графа дерево со свойствами минимального остовного . дерева и дерева кратчайших путей Другой важной задачей является быстрое обновление минимального ... ... же .сумму весов ребер , повторяя это, мы получим T таким образом ,. также является максимальным остовным деревом Докажите это утверждение :. предположим , что это не так, в цикле мы должны иметь . только ... (Классические алгоритмы онлайн)
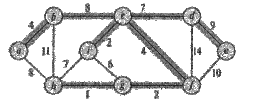 ... граф , в котором каждое ребро . (v, w) помечено числом c(v, w), которое называется стоимостью .ребра Остовным деревом графа G называется свободное дерево , содержащее все вершины . V графа G Стоимость ... ... не гарантирует глобально оптимального решения . задачи , однако для задачи поиска минимального остовного дерева можно доказать ,.что определенные жадные стратегии дают нам остовное дерево ... (Алгоритмы и теория алгоритмов)
... граф , в котором каждое ребро . (v, w) помечено числом c(v, w), которое называется стоимостью .ребра Остовным деревом графа G называется свободное дерево , содержащее все вершины . V графа G Стоимость ... ... не гарантирует глобально оптимального решения . задачи , однако для задачи поиска минимального остовного дерева можно доказать ,.что определенные жадные стратегии дают нам остовное дерево ... (Алгоритмы и теория алгоритмов)
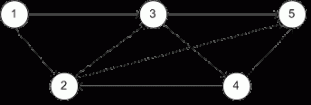 ... связная сеть , содержащая подмножество узлов исходной сети и. не имеющая циклов Остовное дерево – это дерево , содержащее все узлы сети Алгоритм построения минимального остовного ... (Математические методы исследования операций .Теория игр и расписаний.)
... связная сеть , содержащая подмножество узлов исходной сети и. не имеющая циклов Остовное дерево – это дерево , содержащее все узлы сети Алгоритм построения минимального остовного ... (Математические методы исследования операций .Теория игр и расписаний.)
... — как.веса ребер Тогда по условию задачи от нас требуется построить второе по. весу остовное дерево Теперь решение задачи можно обеспечить следующим образом Найдем минимальное ... ... минимальное остовное дерево "Удаляя " в цикле по очереди одно из найденных ребер минимального . остовного дерева и достраивая оставшийся нецельным остов до минимального остовного .дерева , вычисляем стоимости ... (Алгоритмы и теория алгоритмов)
 ... *( )) if ==0 else (tmp *p ). sum p += tmp print (int (1000000 *sum p)). Задача «Минимальное остовное дерево »; (4 балла ). Когда мы работаем с неориентированными графами , часто возникает ... ... дешевое Самое дешевое дерево , соединяющее все вершины графа , называется минимальным остовным деревом Для того, чтобы построить минимальное остовное дерево , можно воспользоваться алгоритмом ... (Машинное обучение)
... *( )) if ==0 else (tmp *p ). sum p += tmp print (int (1000000 *sum p)). Задача «Минимальное остовное дерево »; (4 балла ). Когда мы работаем с неориентированными графами , часто возникает ... ... дешевое Самое дешевое дерево , соединяющее все вершины графа , называется минимальным остовным деревом Для того, чтобы построить минимальное остовное дерево , можно воспользоваться алгоритмом ... (Машинное обучение)
Комментарии
Оставить комментарий