Ортогональный - понятие и значение

Рассмотрим что означает понятие и значение слова ортогональный (информация предоставлена intellect.icu).

Мат.

Расположенный под прямым углом, перпендикулярный.

{Греч. 'ορθογώνιος}

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "ортогональный":
абажурный, абактинальный, абдикационный, абдоминальный, аберрационный, абинный, абиогенный, абиссальный, абнормальный, абонементный, боскетный, голосемянный, званый, малосемейный, несравненный, полубольный, хлебный, чебуречный, швейный

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "ортогональный" :
ланелоный, леныдиный, жйсиденый, нюшаменый, чотабоный, нувогеный, дадажаный, мочеваный.


Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Ортогональный" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-О632, для metaphone-"aртaгaналнaй" и для double-metaphone ARTK.

См. также

... Интеграл по ортогональной случайной мере ( конечной и -конечной структурной . меры ... (вероятностные процессы)

... ПОСТРОЕНИЕ ТЕНЕЙ ПРИПАРАЛЛЕЛЬНОМ ПРОЕЦИРОВАНИИ Припостроении теней вортогональных иаксонометрических проекциях чаще используется .солнечное освещение Построение теней сводится копределению ... (Начертательная геометрия и инженерная графика)

... называется проекцией вектора x на подпространство . L Из предыдущего видно , что совокупность M всех векторов , ортогональных подпространству . L есть также подпространство , которое называется ортогональным дополнением к подпространству .L и обозначается H - L; говорят ... ... есть проекция . элемента x на подпространство M Теорема дает , таким образом , разложение на два взаимно дополнительных ортогональных . подпространства Теорема Для того чтобы линейное многообразие М было всюду плотно . в Н, необходимо ... (Функциональный анализ)

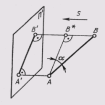... случай проецирования параллельного , когда все .проецирующие лучи перпендикулярны плоскости проекций Ортогональным проекциям присущи все свойства параллельных проекций , ноприпрямоугольном .проецировании проекция отрезка ... ... способы дополнения однопроекционного чертежа Вданном курсе будут рассмотрены чертежи , получаемые ортогональным проецированием на.две илиболее взаимно перпендикулярные плоскости проекций (комплексные чертежи ) и.путем ... (Начертательная геометрия и инженерная графика)

... Теорема Площадь ортогональной проекции многоугольника на плоскость равна произведению его. площади на косинус угла между плоскостью многоугольника ... (Стереометрия)

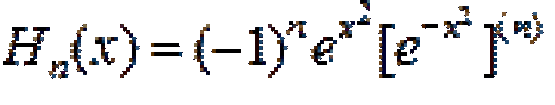... Эти определения согласуются с обычными формулами аналитической геометрии Два вектора х и y ÎН называются ортогональными (в этом. случае записывают ), если Если и , то это определение , в соответствии с общим определением . угла между векторами , означает , что x и y образуют ... ... с общим определением . угла между векторами , означает , что x и y образуют угол .в Нулевой вектор оказывается ортогональным любому вектору х ÎН В пространстве условие ортогональности векторов и имеет вид Легко проверить , вычислив ... (Функциональный анализ)

---

---