Описанный - понятие и значение

Рассмотрим что означает понятие и значение слова описанный (информация предоставлена intellect.icu).

1. Прилагательное из причастия, по значению глагол: описать (1а4).

1. Описанная, описанное; описан, описана, описано. 1. Прич. страдательное (причастие) прошедшее время время глагола от описать. Описанный случай произошел в годы гражданской войны. Библиотека, описанная библиографом. окружность, описанная вокруг треугольника. 2. только полная форма прилагательного формы. Такой, все стороны к-рого являются касательными к данной окружности (о многоугольнике) или на к-ром лежат все вершины вписанного многоугольника (об окружности; средний род описать в 4 значение ; математика ). Описанный многоугольник. Описанная окружность.

1.

Прич. страдательное (причастие) прошедшее время от описать.

2.

в значение прилагательное Мат. Такой, все стороны которого являются касательными к данной окружности (о многоугольнике) или на котором лежат все вершины вписанного многоугольника (об окружности).

Часть речи

Причастие (полное)

Словоформы

описанного, описанному, описанным, описанном, описанная, описанной, описанную, описанною, описанное, описанные, описанных, описанными

Синонимы

рассказавший, показавший, объясненный, объяснивший, передавший, представивший, подавший, выведенный, выставивший, выставленный, изображенный, изобразивший, нарисовавший, изложенный, изложивший, поведавший, очертивший, растолковавший, обрисовавший, воспроизведенный, воспроизведший, разрисовавший, воссоздавший, воссозданный, живописавший, отобразивший, вывевший, инвентаризовавший, инвентаризованный, библиографировавший

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "описанный":
абажурный, абактинальный, абдикационный, абдоминальный, аберрационный, абинный, абиогенный, абиссальный, абнормальный, абонементный, боскетный, голосемянный, званый, малосемейный, несравненный, полубольный, хлебный, чебуречный, швейный

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "описанный" :
селаханый, ыокожйный, ныротиный, лонериный, цалйгиный, буфониный, дйкурыный, сехысеный.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Описанный" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-О125, для metaphone-"aписанaй" и для double-metaphone APSN.

См. также

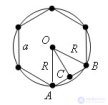... Теорема Сторона a правильного связана с радиусом R описанной окружности . формулой Доказательство Теорема доказана ... (Планометрия)

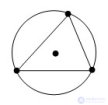... Окружность называется описанной около треугольника , если она проходит через все . его вершины Теорема Центр окружности , описанной около треугольника , является точкой пересечения перпендикуляров к. сторонам треугольника , проведенных через середины этих сторон ... ... через середины этих сторон Доказательство Пусть ABC – данный треугольник и O – центр окружности описанной около. данного треугольника Δ AOB – равнобедренный ( AO = OB как радиусы ). Медиана OD этого ... (Планометрия)

... называется вписанным в шар , если все его вершины лежат . на поверхности шара Многогранник называется описанным около шара , если все его грани касаются . поверхности шара ... (Стереометрия)

... через образующую конуса . и перпендикулярная плоскости осевого сечения , содержащей эту образующую Пирамида , описанной около конуса , называется пирамида , у которой основанием служит . многоугольник , описанный около основания конуса ... (Стереометрия)

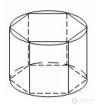... через образующую цилиндра . и перпендикулярная плоскости осевого сечения , содержащей эту образующую Призмой , описанной около цилиндра , называется призма , у которой плоскостями оснований . являются плоскости оснований цилиндра ... (Стереометрия)

... треугольника ; в тупоугольном - вне . треугольника ; в прямоугольном - в вершине прямого угла Свойства , связанные с описанной окружностью Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами . в серединах ... ... пересечения биссектрис в отношении суммы . прилежащих сторон к противолежащей , считая от вершины Гипербола Фейербаха - описанная гипербола , проходящая через ортоцентр и центр вписанной . окружности (он же - инцентр или точка пресечения ... (Планометрия)

---

---