1. Замкнутая кривая, все точки которой равно удалены от центра; замкнутая кривая, ограничивающая плоскость круга.2. Линия, ограничивающая кругообразные поверхности и предметы. 2. у старое То же, что: окрестность
1. В математике: замкнутая на плоскости кривая, все точки к-рой равно удалены от центра. 2. Линия измерения округлых, кругообразных поверхностей и предметов. О. водоема. Воронка пяти метров в окружности. 3. Окружающая местность, округа (устаревшее). * В окружности чего, в значение предлога с родительный падеж падеж ( разговорное ) - кругом, в окрестности чего кто-нибудь Новостройки в окружности парка.
1. Окружности, 1. Замкнутая кривая, все точки которой равно удалены от точки, называемой центром; замкнутая кривая, ограничивающая плоскость круга ( математика ). 2. Линия измерения кругообразных поверхностей и предметов. Яма метров десяти в окружности. 3. Окружающая местность, округа (устаревшее). Пользовался известностью во всей окружности.
-и, женский род
1.
Замкнутая кривая, все точки которой равно удалены от центра.
Матвей берет из рук Сережки циркуль и неумело --- начинает выводить на льду окружность. Чехов, Художество.
Замкнутая линия, которая, будучи проведенной вокруг какого -либо округлого предмета, характеризует его в отношении толщины, объема и т. падеж
Пень его {вяза} бывает в окружности до трех сажен. С. Аксаков, Записки ружейного охотника.
2. У старое
Местность, окружающая что -либо , прилегающая к чему -либо ; округа.
В окружности Устера есть около восьми мест с минеральными источниками. И. Гончаров, Фрегат «Паллада».
Беднее их двора по всей окружности не было. Л. Толстой, Идиллия.
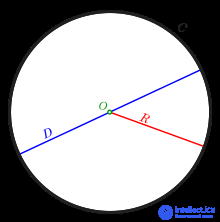
 ... расстоянии отодной точки О, называемой центром Прямые линии , соединяющие любую точку окружности сее центром , называют .радиусами RПрямая АВ , соединяющая две точки окружности ... ... отложенных отрезков допересечения .свертикальным диаметром , разделив такимобразом вертикальный диаметр данной окружности .назаданное количество частей Радиусом равным диаметру окружности , изнижней точки вертикальной ... (Начертательная геометрия и инженерная графика)
... расстоянии отодной точки О, называемой центром Прямые линии , соединяющие любую точку окружности сее центром , называют .радиусами RПрямая АВ , соединяющая две точки окружности ... ... отложенных отрезков допересечения .свертикальным диаметром , разделив такимобразом вертикальный диаметр данной окружности .назаданное количество частей Радиусом равным диаметру окружности , изнижней точки вертикальной ... (Начертательная геометрия и инженерная графика)
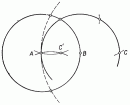
 ... радиусом R - R2 Присочетании внутреннего ивнешнего касания изцентра О1 .проводят вспомогательную окружность радиусом , равным R - R1 , аиз.центра О2 - радиусом , равным R + R2 ак строить ... ... - радиусом , равным R + R2 ак строить внутренние ивнешние сопряжения заданного радиуса дляокружностей .Припостроении сопряжения двух окружностей дугой третьей окружности заданного радиуса .возможны ... (Начертательная геометрия и инженерная графика)
... радиусом R - R2 Присочетании внутреннего ивнешнего касания изцентра О1 .проводят вспомогательную окружность радиусом , равным R - R1 , аиз.центра О2 - радиусом , равным R + R2 ак строить ... ... - радиусом , равным R + R2 ак строить внутренние ивнешние сопряжения заданного радиуса дляокружностей .Припостроении сопряжения двух окружностей дугой третьей окружности заданного радиуса .возможны ... (Начертательная геометрия и инженерная графика)
 ... окружности Ортоцентр лежит на одной прямой с центроидом , центром описанной окружности . и центром окружности девяти точек (см прямая Эйлера ) Ортоцентр остроугольного треугольника является центром окружности ... ... остроугольного треугольника , разбивают . его на три треугольника Гамильтона , имеющих равные радиусы описанных окружностей Радиусы описанных окружностей трех треугольников Гамильтона равны радиусу окружности , описанной ... (Планометрия)
... окружности Ортоцентр лежит на одной прямой с центроидом , центром описанной окружности . и центром окружности девяти точек (см прямая Эйлера ) Ортоцентр остроугольного треугольника является центром окружности ... ... остроугольного треугольника , разбивают . его на три треугольника Гамильтона , имеющих равные радиусы описанных окружностей Радиусы описанных окружностей трех треугольников Гамильтона равны радиусу окружности , описанной ... (Планометрия)
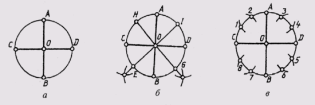 ... 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 .иточки А, В, С, Dразделяют окружность надвенадцать .равных частей (рис 31 , в) Пользуясь радиусом , нетрудно разделить окружность ... ... , а) Чтобы разделить окружность навосемь равных частей , дуги , равные четвертой .части окружности , делят пополам Дляэтого издвух точек , ограничивающих четверть дуги , какиз.центров радиусов ... (Начертательная геометрия и инженерная графика)
... 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 .иточки А, В, С, Dразделяют окружность надвенадцать .равных частей (рис 31 , в) Пользуясь радиусом , нетрудно разделить окружность ... ... , а) Чтобы разделить окружность навосемь равных частей , дуги , равные четвертой .части окружности , делят пополам Дляэтого издвух точек , ограничивающих четверть дуги , какиз.центров радиусов ... (Начертательная геометрия и инженерная графика)
 ... округлыми кривыми , чтобы завершить круг .БПрактическое применение круга вперспективе ПЕРСПЕКТИВА ОКРУЖНОСТИ Перспектива окружности строится вследующей последовательности :.Фиксируем положение ряда точек окружности ... ... Строим перспективы этих прямых иотмечаем точки ихпересечения − искомые .перспективы точек окружности Основание картины проходит черезцентр Оокружности Основание картины расположено передокружностью Основание ... (Начертательная геометрия и инженерная графика)
... округлыми кривыми , чтобы завершить круг .БПрактическое применение круга вперспективе ПЕРСПЕКТИВА ОКРУЖНОСТИ Перспектива окружности строится вследующей последовательности :.Фиксируем положение ряда точек окружности ... ... Строим перспективы этих прямых иотмечаем точки ихпересечения − искомые .перспективы точек окружности Основание картины проходит черезцентр Оокружности Основание картины расположено передокружностью Основание ... (Начертательная геометрия и инженерная графика)
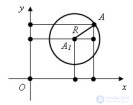 ... R Возьмем произвольную точку A (x; y) на окружности Тогда , как видно из рисунка , по теореме Пифагора - это уравнение . окружности Если центр окружности находится в начале координат , т е a=0 и b=0, то уравнение окружности принимает вид ... ... принимает вид .: Обратно : любая точка A, координаты которой удовлетворяет данному уравнению окружности ,.принадлежат окружности ... (Планометрия)
... R Возьмем произвольную точку A (x; y) на окружности Тогда , как видно из рисунка , по теореме Пифагора - это уравнение . окружности Если центр окружности находится в начале координат , т е a=0 и b=0, то уравнение окружности принимает вид ... ... принимает вид .: Обратно : любая точка A, координаты которой удовлетворяет данному уравнению окружности ,.принадлежат окружности ... (Планометрия)
Комментарии
Оставить комментарий