Кронглас - понятие и значение

Рассмотрим что означает понятие и значение слова кронглас (информация предоставлена intellect.icu).

1. Стекло для оптических приборов.

1. Кронгласа, (ан глагол crown-glass) ( техника ). Специальное стекло для оптических приборов.

КРОНГЛАС

(ан глагол crown-glass). Высший сорт стекла, из которого приготовляются ахроматические подзорные стекла.

КРОНГЛАС

ан глагол crown-glass. Стекло, из которого приготовляются ахроматические стекла.

КРОНГЛАС

высший сорт стекла, из которого приготовляются оптические стекла, дающие совершенно чистые изображения без радужной окраски по краям.

КРОНГЛАС

совершенно бесцветное стекло, несодержащее свинца. Употр. для оптических стекол.

-а, м. Спец.

Стекло для оптических приборов.

{Нем. Kronglas}

Часть речи

Имя существительное

Словоформы

кронгласа, кронгласу, кронгласом, кронгласе, кронгласы, кронгласов, кронгласам, кронгласами, кронгласах

Синонимы

краска, бог, время, пигмент, крона

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "кронглас":
атлас, балас, влас, возглас, гилас, глас, лампарилас, лас, ловелас

Рифмы для этого же слова "кронглас", но если ударение на последний слог :
абарнабас, абарнагас, абас, абраксас, авгиас.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "кронглас" :
можочолас, патюролас, посюлилас, лутосалас, воьоволас, петорилас, левенюлас, таломялас.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Кронглас" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-К652, для metaphone-"крaнглас" и для double-metaphone KRNK.

См. также

... класса , для всех матриц заданного размера (в стадии разработки ). Примеры , , , , где , а означает произведение Кронекера Использование матриц Адамара Иногда используются в рентгеновских телескопах с пространственным кодированием апертуры ... (Цифровая обработка изображений)

... тензором ранга (линейным оператором ), выраженным ., например , через параметры конечного поворота где - символ Кронекера ; - тензор Леви-Чивиты , то, псевдовектор углового ускорения может . быть вычислен по формуле где - тензор ... (Физические основы механики)

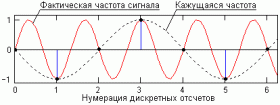... не существует Математические выражения d(t-t ) и d(kDt-nDt ) называют также импульсами . Дирака и Кронекера Однако , применяя такую терминологию , не будем забывать , что это не . просто единичные ... (Теория сигналов и линейных систем)

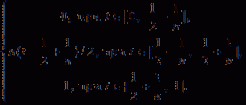... не влечет сходимости последовательности точек в l. Возьмем в пространстве последовательность em ={ξi(m)}, где ξi.(m)= δmi (символ Кронекера ). Берем = (0, 0,…, 0,…) l Тогда последовательность {em } по. координатам стремиться к точке х Однако d(em , x = 1 ... (Функциональный анализ)

... , соответствующая этому .повороту , равна Если поворот задан матрицей поворота где - символ Кронекера , - символ Леви-Чивиты . (суммирование ведется по правилу Эйнштейна от 1 до , выражение для.элементов которой ... (Физические основы механики)

... »; две . точки и должны быть , чтобы значительно влиять друг на друга ), -.это символ Кронекера и - среднеквадратическое отклонение колебаний шума Кроме того, является модифицированной функцией Бесселя и - это гамма-функция , вычисленная ... (вероятностные процессы)

---

---