Коллинеарно - понятие и значение

Рассмотрим что означает понятие и значение слова коллинеарно (информация предоставлена intellect.icu).

Тоже самое что слово - параллельно,

1. Нареч. Соотносится по значение с прилагательное : параллельный (2-5).

Нареч. к параллельный (во 2 и 4 значение ).

{Мы} любовались длинною, идущею параллельно с берегом, кедровою аллеею. И. Гончаров, Фрегат «Паллада».

— Один мой знакомый, — сказал он, — желая изучить новые языки, положил перед собой французское, немецкое и латинское евангелия, читал их параллельно. Чехов, Дорогие уроки.

Синонимы

один, вместе, общий, одновременно, одновременный, соответствующий, одинаковый, наплевать, безразлично, сопутствующий, враз, синхронный, единовременно, единовременный, в одно время, в то же время, все равно, симультанный, соответствующе, раз, сразу, синхронно, симультанно, без разницы, до звезды, имел я ввиду, когерентно, меня не колышет, мне хоть потоп, параллельно

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "коллинеарно":
авантюрно, аверно, авторитарно, ажурно, амбулаторно, априорно, архитектурно, безалаберно, безбурно, бездарно, зерно, катерно, серно, скверно, смирно, черно

Рифмы для этого же слова "коллинеарно", но если ударение на последний слог :
абиогенно, абсолютно, абстрактно, абсурдно, авантажно.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "коллинеарно" :
тапеморно, рютеыирно, сещулорно, нолалярно, ьоьысерно, бамилюрно, тупенырно, заьоверно.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Коллинеарно" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-К456, для metaphone-"кaлиниарнa" и для double-metaphone KLNR.

См. также

... Два ненулевых вектора называются коллинеарными , если они лежат на одной . прямой или на параллельных прямых Коллинеарные векторы либо одинаково направлены , либо противоположно направлены ... (Планометрия)

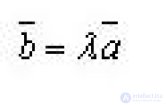... Теорема Если есть два отличных от нуля коллинеарных вектора , то. существует число λ такое , что Доказательство Пусть a и b одинаково направлены - это векторы , которые ... (Планометрия)

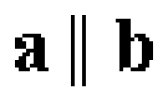... базиса см [1 , 3 , Два вектора a, b , параллельные одной прямой , называются коллинеарными (обозначение .: ) Если векторы рассматриваются на плоскости , то неколлинеарные векторы a, b. также называются базисом ... (Линейная алгебра и аналитическая геометрия)

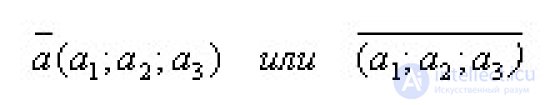... Коллинеарные векторы могут иметь совпадающие или противоположные направления Нулевой вектор считают коллинеарным любому вектору Векторы называются равными , если они коллинеарны , одинаково направлены и имеют . одинаковые ... ... плоскостях Если среди трех векторов хотя бы один нулевой или два . любые коллинеарны , то такие векторы компланарны Рассмотрим в пространстве прямоугольную систему координат Выделим на осях координат ... (Стереометрия)

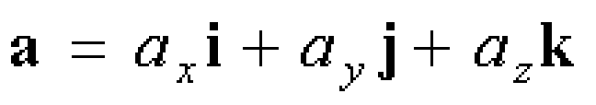... Пусть в ПДСК заданы векторы ,. Тогда ;,α - вещественное число Векторы αa и a являются коллинеарными , если α > 0, их. направления совпадают , если α < 0, их направления противоположны ... (Линейная алгебра и аналитическая геометрия)

... с этими осями при , или ). Действительно , направляющие векторы рассматриваемых прямых имеют координаты , или , или , очевидно ., что они коллинеарны векторам , или , или соответственно , где - направляющие векторы .координатных прямых Посмотрите иллюстрации к этим частным ... ... . и , то есть, (при необходимости смотрите нахождение координат вектора по.координатам точек ) Теперь записываем условие коллинеарности векторов и :. , где λ - произвольное действительное число (при точки и совпадают , что. нас тоже устраивает ) Если ... (Линейная алгебра и аналитическая геометрия)

---

---